Redovisning av obligationer betalas

• Text
• problem
• mål prestation
• fyll i ämnena
• flervalsfrågor
• ordlista

en obligation betalas är bara ett löfte att betala en serie betalningar över tiden (räntekomponenten) och ett fast belopp vid förfallodagen (det nominella beloppet). Således är det en blandning av en livränta (räntan) och klumpsumma (ansiktet)., För att bestämma det belopp som en investerare kommer att betala för en obligation, kräver därför nuvärdesberäkningar för att bestämma det nuvarande värdet av de framtida betalningarna. Antag att Schultz företag utfärdar 5-år, 8% obligationer. Obligationer har ofta en $ 1,000 nominellt värde och betala ränta var sjätte månad., Med hjälp av dessa antaganden, överväga följande tre alternativa scenarier:

följande tabell visar beräkningar av priset på obligationen under olika scenarier:

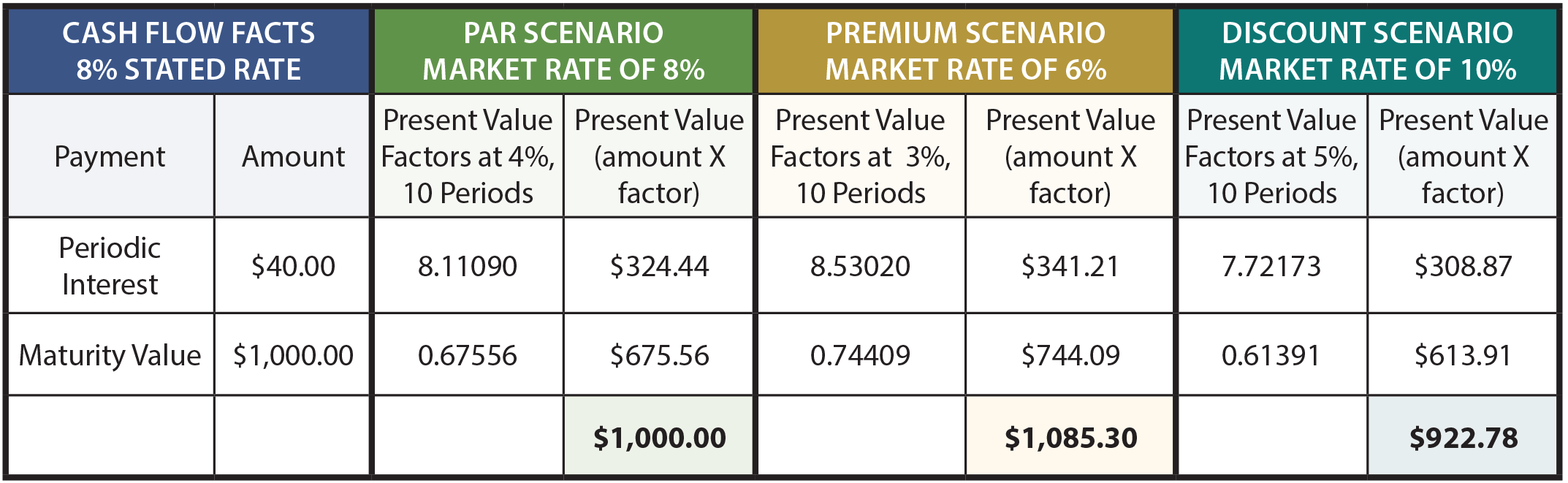
för att ytterligare förklara är räntebeloppet på $1,000, 8% – obligationen $40 var sjätte månad. Eftersom obligationerna har en 5-årig livstid finns det 10 räntebetalningar (eller perioder)., Den periodiska räntan är en livränta med en löptid på 10 år, medan löptidsvärdet är en klumpsumma vid slutet av den tionde perioden. Marknadsräntan på 8% motsvarar en halvårskurs på 4%, marknadsräntan på 6% motsvarar en halvårskurs på 3% och 10% är 5% per halvårsperiod.

nuvärdesfaktorerna tas från nuvärdestabellerna (livränta respektive klumpsumma). Ta dig tid att verifiera faktorerna med hänvisning till lämpliga tabeller, kalkylblad eller kalkylator rutin., Nuvärdesfaktorerna multipliceras med betalningsbeloppen, och summan av nuvärdet av komponenterna skulle motsvara priset på obligationen enligt vart och ett av de tre scenarierna.

dessa beräkningar är inte bara korrekta teoretiskt, men är mycket exakta finansiella verktyg. En punkt är dock anmärkningsvärd. Bond prissättning är ofta till närmaste 1/32: a. Det vill säga en obligation kan handla vid 103.08. Man kan lätt misstolka detta pris som $ 1,030.80. Men det betyder faktiskt 103 och 8/32. I Dollar skulle detta uppgå till $ 1,032. 50 ($1,000 X 103.25)., Efter att ha lärt sig obligationernas finansiella mekanik är det nu dags att undersöka rätt redovisning.

obligationer emitterade på Par

om Schultz emitterade 100 av sina 5-årsobligationer på par skulle följande poster krävas :

obligationer emitterade på en premie

en enkelt sätt att förstå obligationer emitterade på en premie är att se redovisningen i förhållande till att räkna pengar!, Om Schultz utfärdar 100 av de 8%, 5-åriga obligationerna när marknadsräntan bara är 6%, är de mottagna kontanterna $ 108.530 (se tidigare beräkningar). Schultz måste återbetala totalt $ 140,000 ($4,000 var sjätte månad i 5 år, plus $ 100,000 vid förfall).

Således kommer Schultz att återbetala $31,470 mer än vad som lånades ($140,000 – $108,530)., Denna $ 31,470 måste spenderas under obligationens livstid; likformigt sprider $ 31,470 över 10 sexmånadersperioder ger periodisk räntekostnad på $ 3,147 (för att inte förväxlas med den faktiska periodiska kontantbetalningen på $4,000).

ett annat sätt att illustrera detta problem är att notera att den totala lånekostnaden minskas med $8.530-premien, eftersom mindre ska återbetalas vid löptid än vad som lånades på framsidan., Därför reduceras $4,000 periodisk räntebetalning med $ 853 av premieavskrivningar varje period ($8.530 premieavskrivningar på rak linje över 10-perioderna), vilket också ger den periodiska räntekostnaden för $3,147 ($4,000 – $853).

det här ämnet är i sig förvirrande och journalposterna klargör faktiskt. Observera att den premie på obligationer som ska betalas tas upp på ett separat konto (till skillnad från redovisning av investeringar i obligationer som omfattas av ett tidigare kapitel, där premien helt enkelt ingick i investeringen på Obligationskontot).,

studera följande illustration och observera att premien på obligationer som ska betalas är fastställd till $8.530, minskas sedan med $853 varje räntedatum, vilket ger slutbalansen till noll vid förfallodagen.

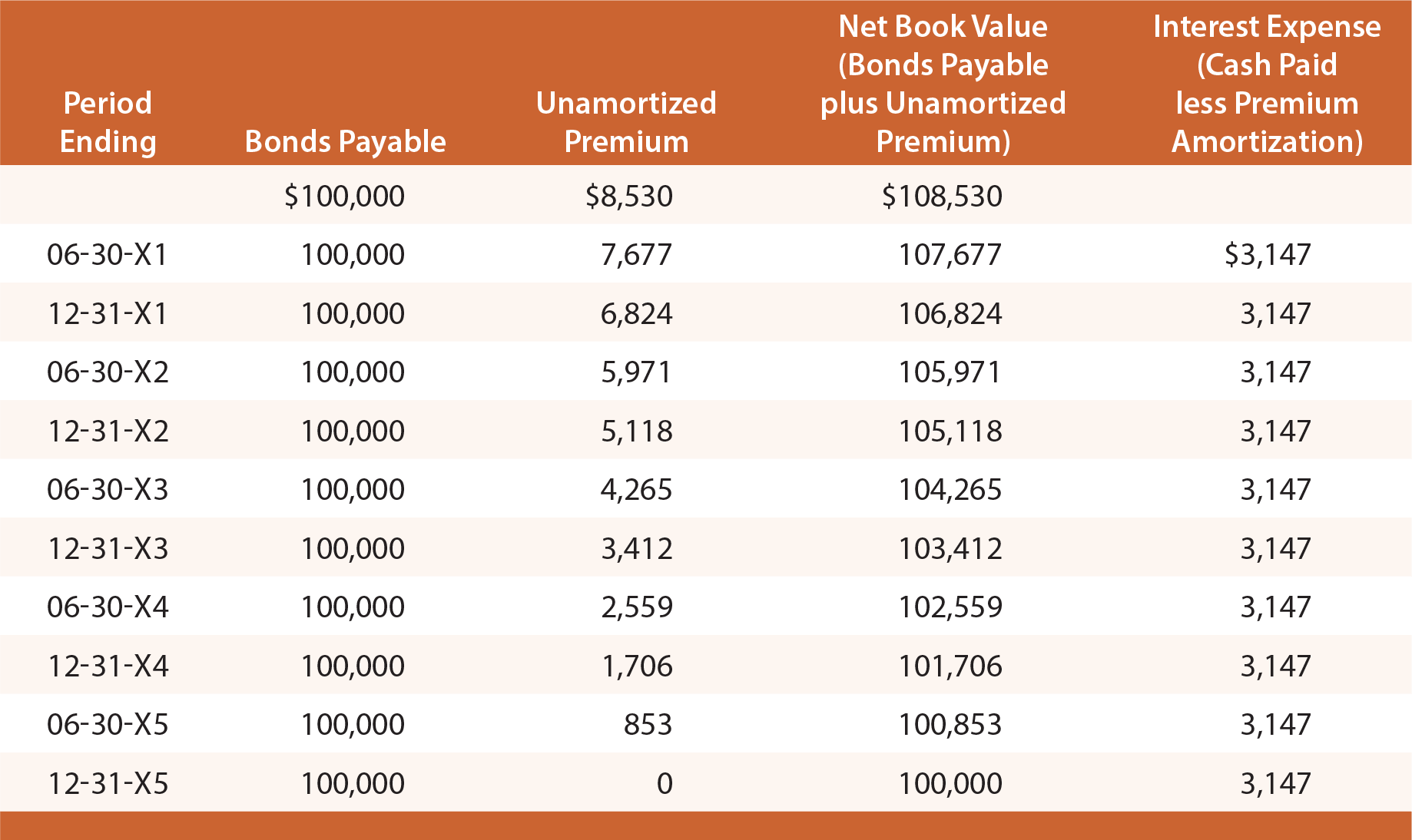
på ett visst bokslutsdatum rapporteras obligationer som ska betalas i balansräkningen som en skuld, tillsammans med det oavskrivna Premiebalansen (känt som ett ”tilläggskonto”)., För att illustrera, balansräkning tilläggsupplysningar skulle visas enligt följande den 31 December 20X3 och 20X4:

resultaträkningen för alla 20X3 skulle omfatta $6,294 av räntekostnader ($3,147 X 2). Denna metod för redovisning av obligationer kallas straight-line amorteringsmetoden, eftersom räntekostnaden redovisas jämnt över obligationens livslängd. Även om det är enkelt, har det en konceptuell brist., Observera att räntekostnaden är densamma varje år, även om det bokförda nettovärdet för obligationen (obligation plus återstående premie) minskar varje år på grund av avskrivningar.

som ett resultat är räntekostnaden varje år inte exakt lika med den effektiva räntan (6%) som var implicit i prissättningen av obligationerna. För 20X1 kan räntekostnaden ses som ungefär 5,8% av obligationsskulden ($6,294 kostnad dividerad med årets början skuld på $ 108,530). För 20X4 är räntekostnaden ungefär 6.,1% ($6,294 kostnad dividerat med början av året ansvar på $ 103,412).

revisorer har utarbetat en mer exakt metod för att ta hänsyn till obligationslån som kallas effektiv ränta. Var medveten om att den mer teoretiskt korrekta effektiva räntemetoden faktiskt är den önskade metoden, utom i de fall där raklinjeresultaten inte skiljer sig väsentligt. Effektiva metoder införs i följande avsnitt i detta kapitel.,

obligationer emitterade med rabatt

ett annat sätt att överväga detta problem är att notera att den totala lånekostnaden ökar med $7,722-rabatten, eftersom mer ska återbetalas vid löptid än vad som ursprungligen lånades. Därför ökas $4,000 periodisk räntebetalning med $ 772.20 av rabatt amortering varje period ($7,722 Rabatt amorteras på en rak linje under de 10 perioderna), producerar periodiska räntekostnader som totalt $ 4,772. 20.

som bondpremier, rabatter också transporteras i ett separat konto., Följande post behövs för att registrera den ursprungliga obligationsemissionen:

följande poster återspeglar periodisk ränta och återbetalning vid förfallodagen:

noggrant studera denna illustration och observera att rabatten på obligationer som ska betalas är fastställd till $7,722 och sedan minskas med $772.20 på varje räntedag, vilket gör det slutliga saldot till noll vid förfallodagen., På ett visst bokslutsdatum redovisas obligationer som ska betalas i balansräkningen som en skuld, tillsammans med den oredovisade Rabatt som subtraheras (känt som ett ”contra” – konto). Illustrationen nedan visar redovisningen av balansräkningen per den 30 juni 20X3. Observera att den obestämda rabatten på detta datum bestäms av beräkningar som visas i tabellen enligt följande:

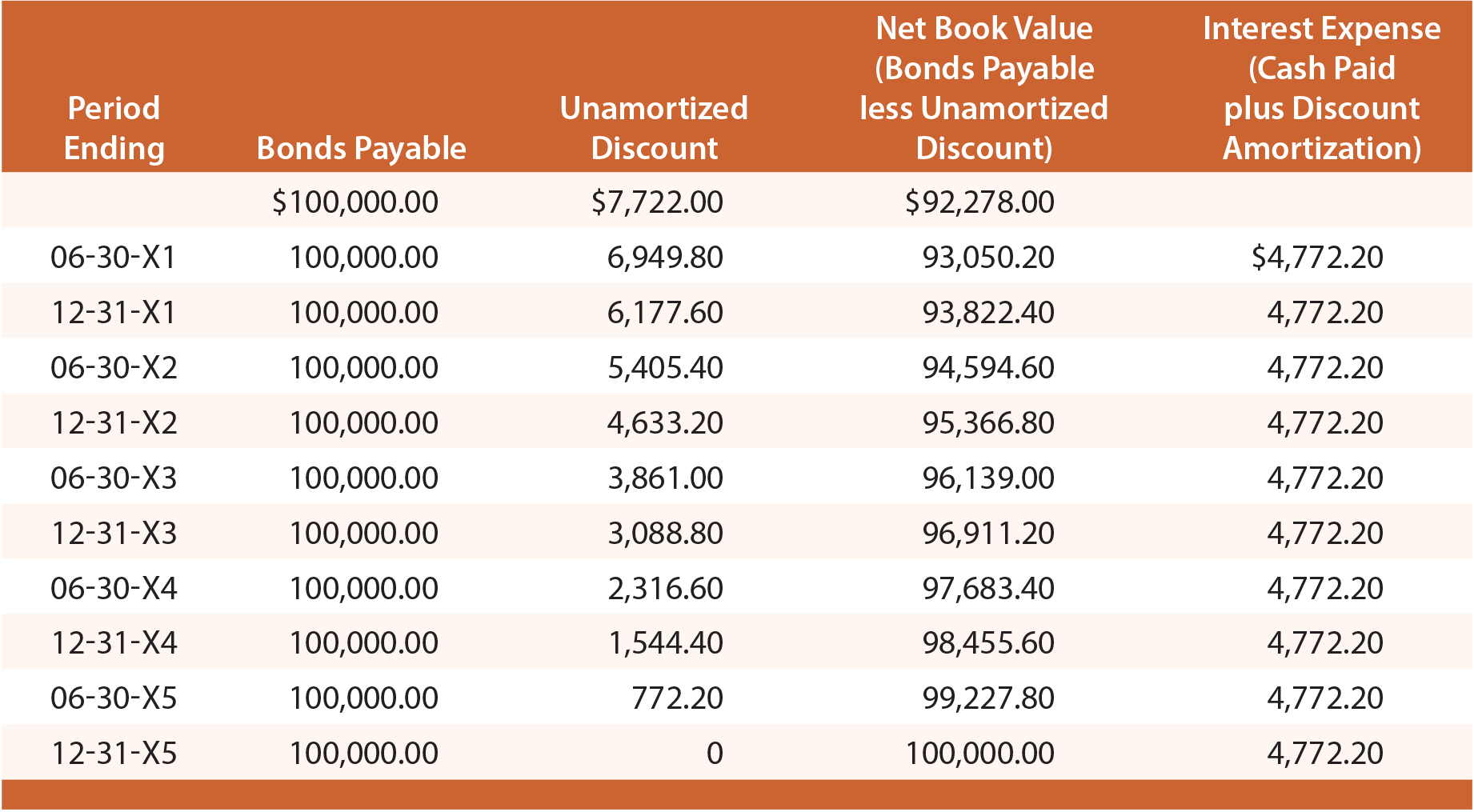
varje årlig resultaträkning skulle omfatta $9.544.40 räntekostnader ($4,772.20 X 2)., Straight-line-tillvägagångssättet lider av samma begränsningar som diskuterats tidigare, och är acceptabelt endast om resultaten inte väsentligt skiljer sig från de som resulterar med effektiv-intresse teknik.