- Texto
- Problemas
- a Conquista de Objetivos
- Preencha os Espaços em branco
- Múltipla Escolha
- Glossário
Um título a pagar é apenas uma promessa de pagar uma série de pagamentos ao longo do tempo (o componente de juros) e de um valor fixo, na data do vencimento (o valor de face). Assim, é uma mistura de uma anuidade (os juros) e pagamento de quantia única (o rosto)., Para determinar o montante que um investidor irá pagar por uma obrigação, portanto, requer cálculos do valor atual para determinar o valor atual dos pagamentos futuros. Suponha que a Schultz Company emite obrigações de 5 anos e 8%. As obrigações têm frequentemente um valor facial de mil dólares e pagam juros a cada seis meses., Usando esses pressupostos, considere as seguintes três cenários alternativos:



a tabela A seguir mostra os cálculos do preço do título, sob diferentes cenários:
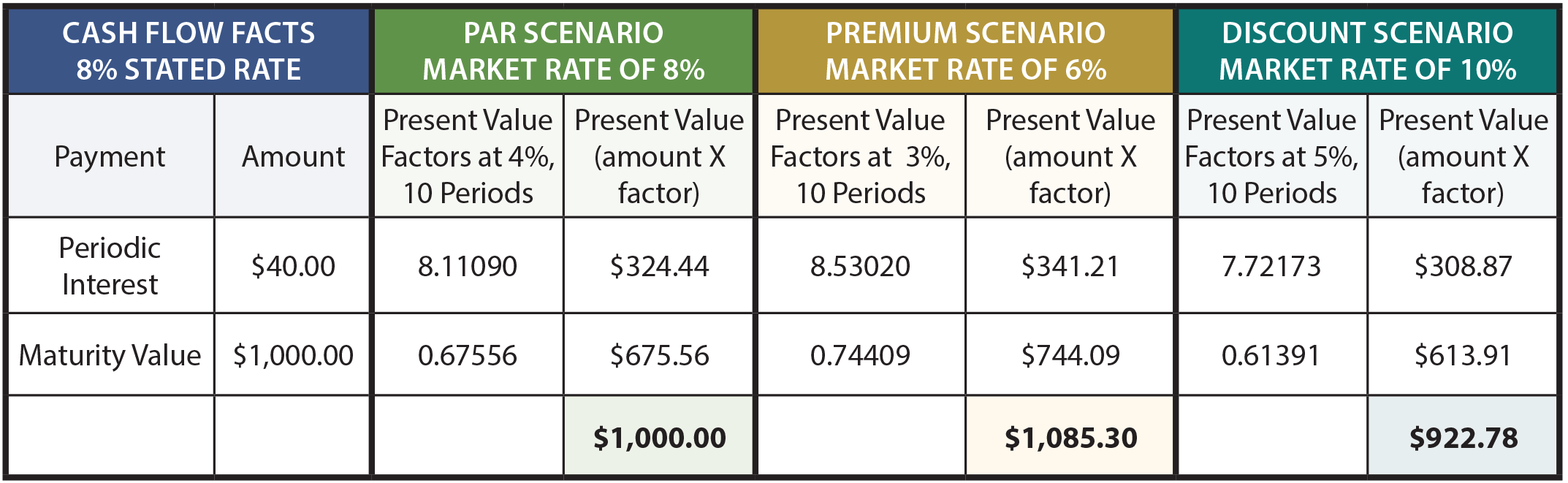
Para explicar, o montante de juro sobre os r $1.000, 8% bond é de r $40 a cada seis meses. Como as obrigações têm uma vida de 5 anos, há 10 pagamentos de juros (ou períodos)., O juro periódico é uma anuidade com uma duração de 10 períodos, enquanto o valor de maturidade é um pagamento de montante fixo no final do décimo período. A taxa de juro de mercado de 8% equivale a uma taxa semestral de 4%, o cenário de taxa de mercado de 6% equivale a uma taxa semestral de 3% e a taxa de 10% é de 5% por período semestral.
os factores de valor actuais são extraídos das tabelas de valores actuais (annuity e lump-sum, respectivamente). Leve tempo para verificar os fatores por referência às tabelas apropriadas, planilha ou rotina da calculadora., Os fatores de valor atuais são multiplicados pelos montantes de pagamento, e a soma do valor atual dos componentes seria igual ao preço da obrigação em cada um dos três cenários.
estes cálculos não são apenas corretos teoricamente, mas são ferramentas financeiras muito precisas. No entanto, um ponto é digno de nota. O preço das obrigações é frequentemente o mais próximo de 1/32. Isto é, uma obrigação pode negociar a 103.08. Pode-se facilmente interpretar este preço como 1,030.80 dólares. Mas, na verdade significa 103 e 8/32. Em Dólares, isso seria de US $ 1,032, 50 (US $ 1,000 X 103,25)., Tendo aprendido a mecânica financeira das obrigações, é agora tempo de examinar a contabilidade correta.
as Obrigações Emitidas Ao Par
Se Schultz emitidos 100 dos seus 5 anos, 8% bônus ao par, as entradas a seguir seria necessário :

de Títulos Emitidos No Premium
Uma forma simples de entender obrigações emitidas em um prêmio é ver a contabilidade em relação à contagem de dinheiro!, Se Schultz emitir 100 dos títulos de 8%, 5 anos quando a taxa de juro do mercado é de apenas 6%, Então o dinheiro recebido é de US $108,530 (veja os cálculos anteriores). Schultz terá que pagar um total de US $140.000 (US$4.000 a cada 6 meses por 5 anos, mais US $100.000 na maturidade).
assim, Schultz vai reembolsar $31,470 mais do que foi emprestado ($140,000 – $108,530)., Este $31,470 deve ser lançado como despesa durante a vida útil do título; espalhar uniformemente a $31,470 mais de 10 períodos de seis meses produz periódica de juros despesa de us $3,147 (para não ser confundido com o real periódica pagamento em dinheiro de us $4.000).
, Portanto, o pagamento periódico de juros de $ 4.000 é reduzido em $ 853 de amortização premium cada período ($8,530 prémio amortizado em uma base de linha reta ao longo dos 10 períodos), também produzindo o custo periódico de juros de$3,147 ($4,000 – $853).
este tópico é inerentemente confuso, e as entradas do diário são realmente esclarecedoras. Notice that the premium on bonds payable is carried in a separate Accounting (unlike accounting for investments in bonds covered in a prior chapter, where the premium was simply included with the Investment in Bonds account).,

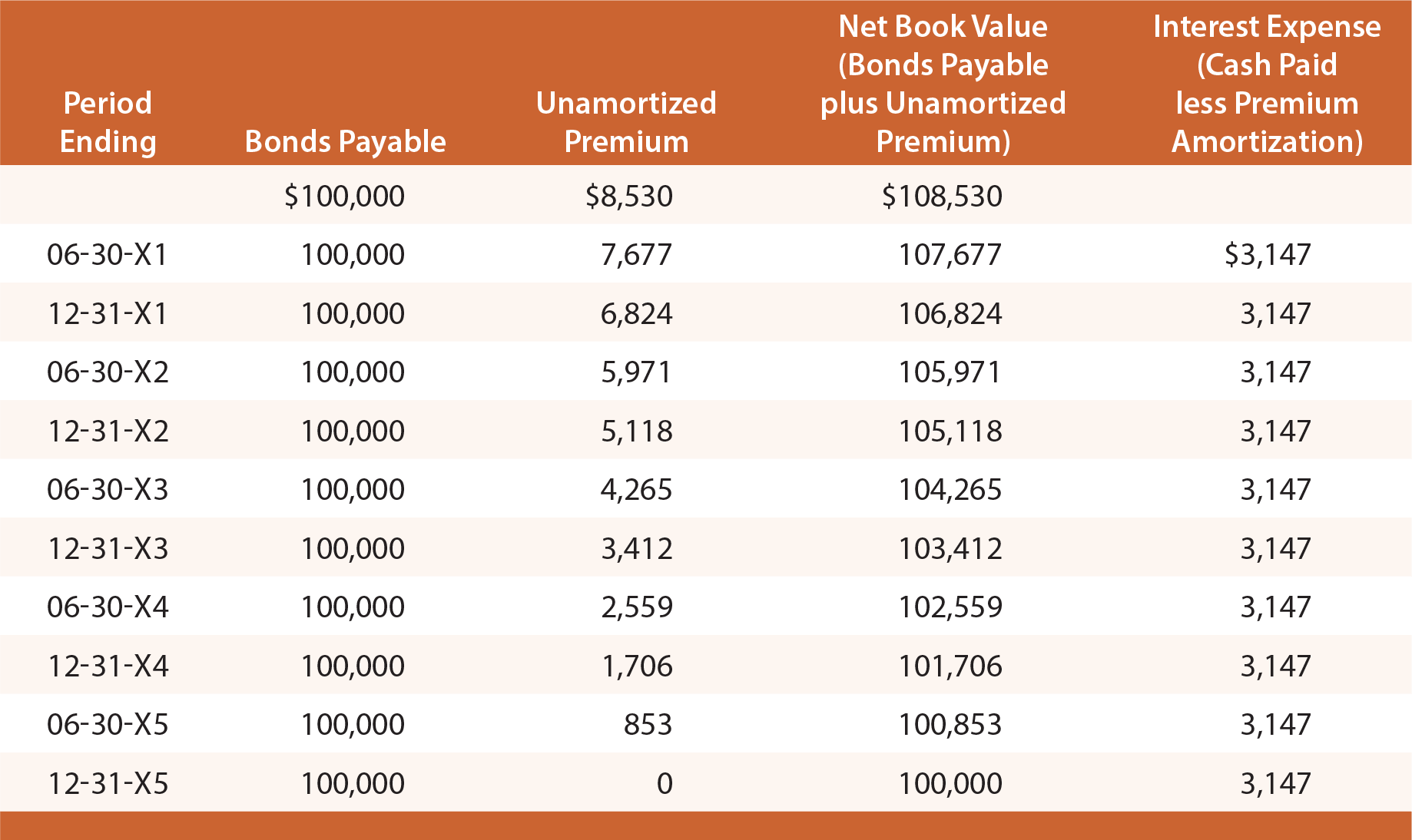
estude a seguinte ilustração, e observe que o prémio sobre as obrigações a pagar é estabelecido em $8,530, depois reduzido em $853 cada data de juro, elevando o saldo final a zero na maturidade.
numa dada data de demonstração financeira, as obrigações a pagar são reportadas no balanço como um passivo, juntamente com o saldo do prémio não amortizado (conhecido como uma conta “adjunta”)., Para ilustrar, a divulgação do balanço apareceria da seguinte forma em 31 de dezembro de 20X3 e 20X4:


A declaração de rendimentos para todos 20X3 incluiria $6,294 de despesas de juros ($3,147 X 2). This method of accounting for bonds is known as the straight-line amortization method, as interest expense is recognized uniformemente over the life of the bond. Embora simples, tem um defeito conceptual., Note – se que as despesas com juros são as mesmas a cada ano, mesmo que o valor contabilístico líquido da Obrigação (obrigação mais Prémio remanescente) esteja a diminuir a cada ano devido à amortização.
como resultado, as despesas com juros a cada ano não são exatamente iguais à taxa de juro Efetiva (6%) que estava implícita no preço das obrigações. For 20X1, interest expense can be seen to be roughly 5.8% of the bond liability ($6,294 expense divided by beginning of year liability of $108,530). Para 20X4, a despesa com juros é de aproximadamente 6.,1% ($6,294 despesa dividida pelo passivo do início do ano de $ 103,412).
Accountants have develop a more precise approach to account for bond issues called the effective-interest method. Esteja ciente de que o método de interesse efetivo mais teoricamente correto é realmente o método requerido, exceto nos casos em que os resultados de linha reta não diferem materialmente. As técnicas de interesse efectivo são introduzidas numa secção seguinte do presente capítulo.,as obrigações emitidas com desconto
outra forma de considerar este problema é notar que o custo total do empréstimo é aumentado pelo desconto de $7.722, uma vez que mais deve ser reembolsado na data de vencimento do que inicialmente. Portanto, o pagamento periódico de juros de $4.000 é aumentado em$772,20 de amortização de desconto a cada período ($7.722 desconto amortizado em uma base de linha reta ao longo dos 10 períodos), produzindo gastos de juros periódicos que totalizam $ 4.772.20.
tal como os prémios de obrigações, os descontos são também contabilizados numa conta separada., A seguinte entrada é necessária para o registro inicial de uma emissão de obrigações:

As seguintes entradas refletir periódico de juros e de reembolso na maturidade:

estudar Cuidadosamente esta ilustração, e observe que o Desconto de Títulos a Pagar, é fixado em $7,722, em seguida, reduzido em $772.20 em cada data interesse, elevando o saldo final a zero na data de vencimento., Numa dada data de balanço financeiro, as obrigações a pagar são reportadas no balanço como um passivo, juntamente com o desconto não amortizado que é subtraído (conhecido como uma conta “contra”). A ilustração abaixo mostra a divulgação do balanço a partir de 30 de junho de 20X3. Observe que o desconto a amortizar, nesta data, é determinado por cálculos revelado na tabela que se segue:

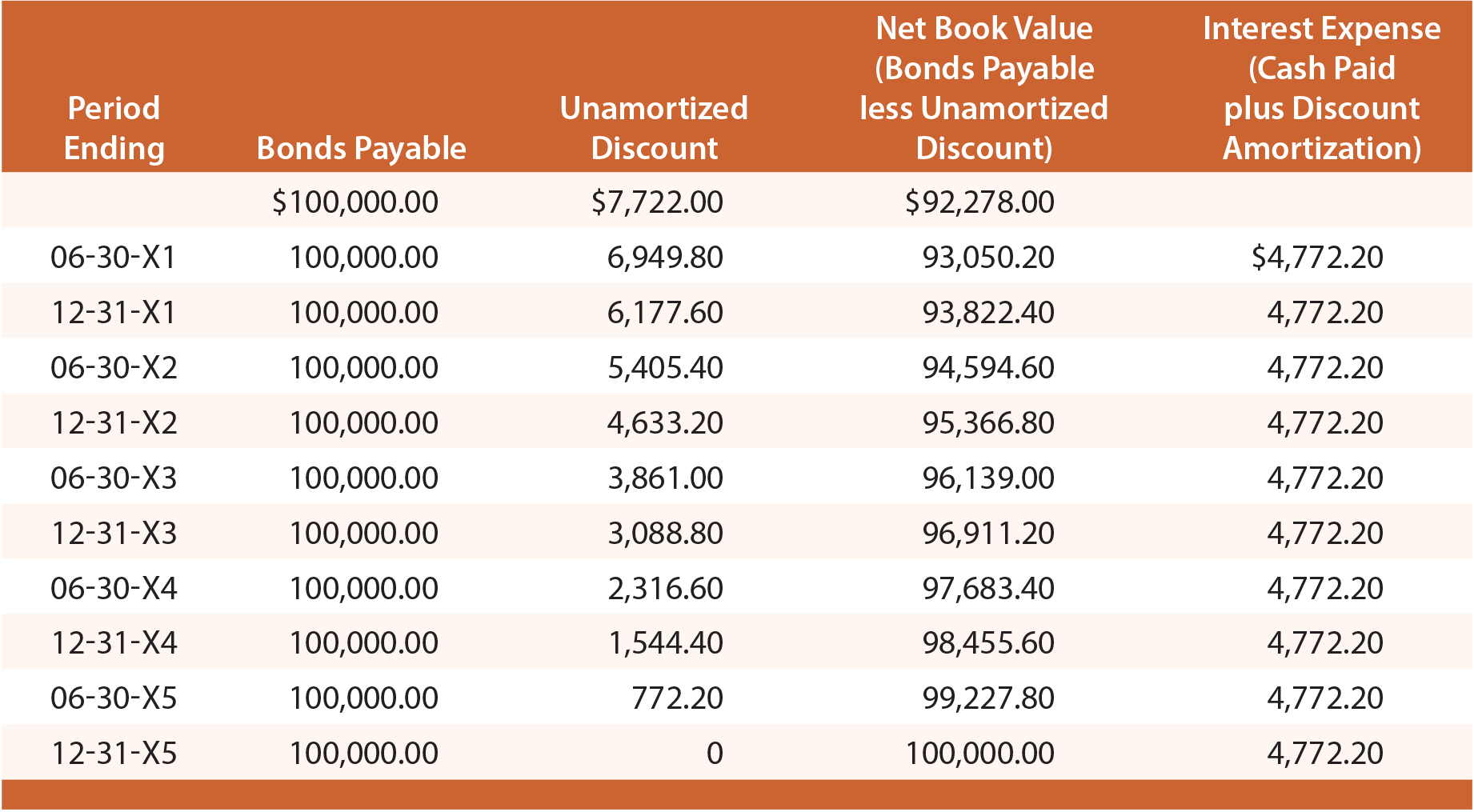
Cada anualmente, declaração de rendimentos incluiria $9,544.40 da despesa de juros ($4,772.20 X 2)., A abordagem de linha reta sofre das mesmas limitações discutidas anteriormente, e só é aceitável se os resultados não forem materialmente diferentes dos resultantes da técnica de interesse efetivo.- aprendeste? – não.
Quais os factores que irão afectar geralmente o preço de emissão de uma obrigação?
entender por que o valor atual é importante para os cálculos de preços de obrigações.
pode calcular o preço de emissão de uma obrigação.
preparar entradas no diário para todo o ciclo de vida de uma obrigação emitida ao par.,
ser capaz de descrever quando uma obrigação é emitida a um prémio, e preparar entradas de jornal para a sua emissão.
Use the straight-line method to account for a bond issued at a premium.
ser capaz de descrever quando uma obrigação é emitida a um desconto, e preparar entradas de jornal para a sua emissão.
Use o método da linha reta para contabilizar uma obrigação emitida a desconto.entende como as obrigações são apresentadas num balanço, quer sejam emitidas ao par, a prémio ou a desconto.