Accounting For Bonds Payable

• tekst
• problemen
• doelstellingen verwezenlijking
• vul de blanco ‘ s in
• Multiple Choice
• Woordenlijst

een te betalen obligatie is slechts een belofte om een reeks betalingen in de tijd (de rentecomponent) en een vast bedrag op de vervaldag (het nominale bedrag) te betalen. Dus, het is een mix van een lijfrente (de rente) en forfaitaire som betaling (het gezicht)., Om het bedrag te bepalen dat een belegger zal betalen voor een obligatie, vereist daarom contante waardeberekeningen om de huidige waarde van de toekomstige betalingen te bepalen. Stel dat Schultz Company 5-jaars obligaties van 8% uitgeeft. Obligaties hebben vaak een $ 1.000 nominale waarde en betalen elke zes maanden rente., Met behulp van deze veronderstellingen, rekening houden met de volgende drie alternatieve scenario ‘ s:

De volgende tabel toont de berekening van de prijs van de obligatie onder verschillende scenario ‘ s:

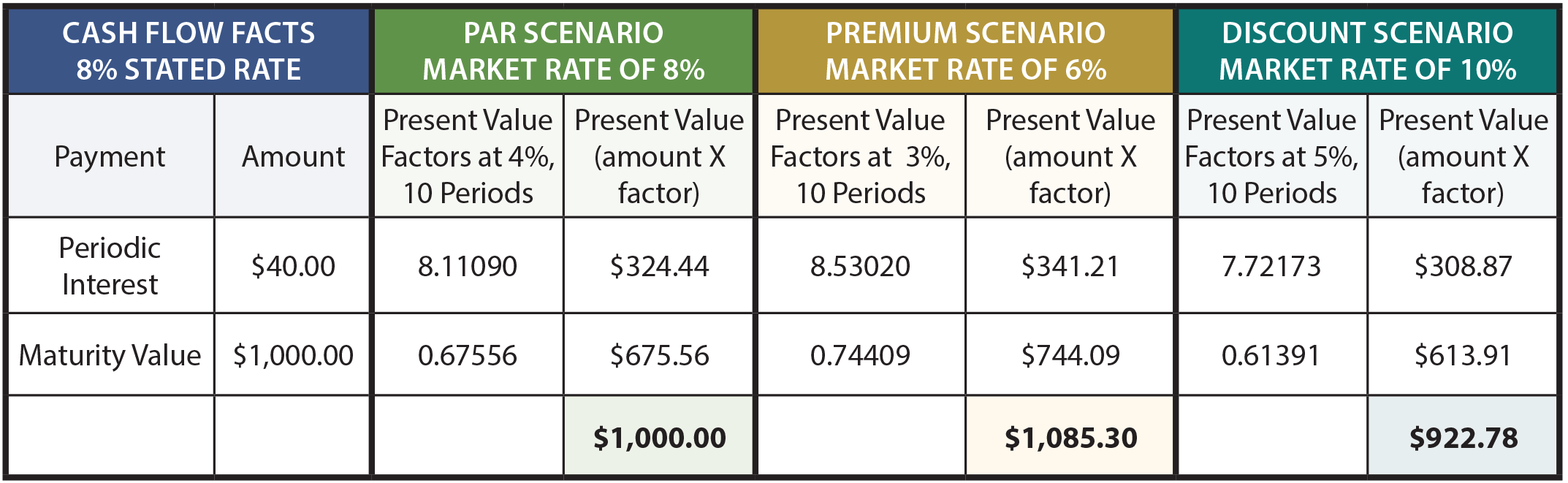
Om verder uit te leggen, het rente bedrag op van $1.000, 8% obligatie is $40 per zes maanden. Omdat de obligaties een looptijd van 5 jaar hebben, zijn er 10 rentebetalingen (of perioden)., De periodieke rente is een lijfrente met een looptijd van 10 maanden, terwijl de looptijdwaarde een forfaitaire betaling is aan het einde van de tiende periode. De marktrente van 8% komt overeen met een halfjaartarief van 4%, Het marktrentescenario van 6% komt overeen met een halfjaartarief van 3% en het tarief van 10% bedraagt 5% per halfjaarperiode.

de contante waardefactoren zijn ontleend aan de contante waardetabellen (lijfrente en forfaitaire som, respectievelijk). Neem de tijd om de factoren te controleren aan de hand van de juiste tabellen, spreadsheet of calculator routine., De contante waardefactoren worden vermenigvuldigd met de betalingsbedragen, en de som van de contante waarde van de componenten zou gelijk zijn aan de prijs van de obligatie onder elk van de drie scenario ‘ s.

deze berekeningen zijn niet alleen theoretisch correct, maar ook zeer nauwkeurige financiële instrumenten. Eén punt is echter opmerkelijk. Obligatieprijzen liggen vaak op de dichtstbijzijnde 1 / 32e. Dat wil zeggen, een obligatie kan handelen op 103.08. Men kan deze prijs gemakkelijk verkeerd interpreteren als $ 1.030. 80. Maar, het betekent eigenlijk 103 en 8/32. In dollars zou dit oplopen tot $ 1.032, 50 ($1.000 X 103.25)., Na de financiële mechanica van obligaties te hebben geleerd, is het nu tijd om de juiste boekhouding te onderzoeken.

Uitgegeven Obligaties Tegen de Nominale

Als Schultz uitgegeven 100 van zijn 5-jaar, 8% obligaties tegen pari, zijn de volgende items vereist :

Obligaties Uitgegeven Tegen Een Premium

Een eenvoudige manier om te begrijpen obligaties uitgegeven tegen een premium is om de boekhouding in vergelijking met het tellen van geld!, Als Schultz 100 van de 8%, 5-jaar obligaties uitgeeft wanneer de marktrente slechts 6% is, dan is het ontvangen kasgeld $ 108.530 (zie de vorige berekeningen). Schultz zal moeten terugbetalen een totaal van $140.000 ($4.000 elke 6 maanden voor 5 jaar, plus $ 100.000 op looptijd).

Schultz zal dus 31.470 dollar meer terugbetalen dan was geleend (140.000 Dollar – 108.530 Dollar)., Deze $31.470 moet worden uitgegeven over de levensduur van de obligatie; uniform spreiden van de $31.470 over 10 perioden van zes maanden produceert periodieke rentelasten van $3.147 (niet te verwarren met de werkelijke periodieke contante betaling van $ 4.000).

een andere manier om dit probleem te illustreren is op te merken dat de totale kosten van de lening worden verminderd met de premie van $8.530, omdat minder op de vervaldag moet worden afgelost dan vooraf werd opgenomen., Daarom wordt de periodieke rentebetaling van $ 4.000 verminderd met $ 853 van premie afschrijving elke periode ($8.530 premie geamortiseerd op een rechte lijn basis over de 10 perioden), ook het produceren van de periodieke rentelasten van $3,147 ($4,000 – $853).

dit onderwerp is inherent verwarrend, en de journaalvermeldingen zijn eigenlijk verhelderend. Merk op dat de premie op te betalen obligaties op een aparte rekening wordt geboekt (in tegenstelling tot de boekhouding voor beleggingen in obligaties die in een eerder hoofdstuk zijn opgenomen, waar de premie gewoon in de rekening voor beleggingen in obligaties is opgenomen).,

Bestudeer de volgende illustratie en merk op dat de premie op te betalen obligaties wordt vastgesteld op $8.530, vervolgens verminderd met $853 op elke Rentedatum, waardoor het eindsaldo op de vervaldag op nul komt.

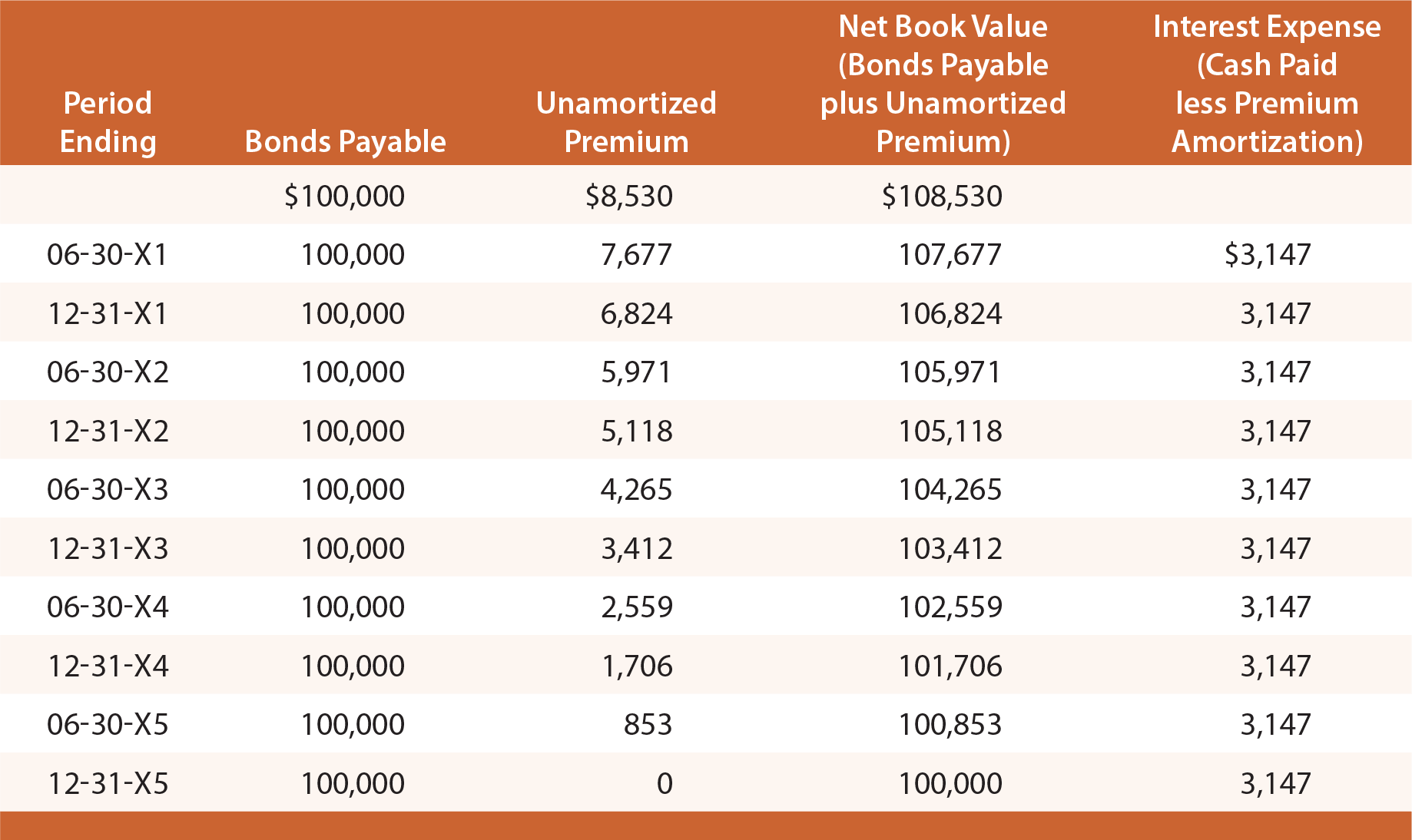
op een gegeven Datum van de jaarrekening worden te betalen obligaties op de balans gerapporteerd als een verplichting, samen met het niet-geamortiseerde Premiesaldo (bekend als een “aanvullende” rekening)., Ter illustratie: de informatie op de balans ziet er op 31, 20X3 en 20X4 als volgt uit:

de winst-en verliesrekening voor alle 20X3 zou 6,294 $aan rentelasten ($3,147 X 2). Deze methode van boekhouding voor obligaties staat bekend als de lineaire afschrijvingsmethode, aangezien rentelasten uniform over de levensduur van de obligatie worden opgenomen. Hoewel het eenvoudig is, heeft het een conceptuele tekortkoming., Merk op dat de rentelasten elk jaar hetzelfde zijn, ook al daalt de netto boekwaarde van de obligatie (obligatie plus resterende premie) elk jaar als gevolg van afschrijvingen.

als gevolg hiervan zijn de rentelasten per jaar niet precies gelijk aan de effectieve rente (6%) Die impliciet was in de prijsstelling van de obligaties. Voor 20X1, rentelasten kunnen worden gezien als ruwweg 5,8% van de obligatieverplichting ($6.294 Last gedeeld door begin van het jaar verplichting van $108.530). Voor 20X4, rentelasten is ongeveer 6.,1% ($6,294 Last gedeeld door Begin jaar aansprakelijkheid van $ 103,412).

Accountants hebben een preciezere aanpak ontwikkeld voor de verantwoording van obligatie-emissies, de zogenaamde effective-interest method. Wees ervan bewust dat de meer theoretisch correcte effectieve-rente methode eigenlijk de vereiste methode is, behalve in die gevallen waarin de lineaire resultaten niet wezenlijk verschillen. Effectieve-rente technieken worden geïntroduceerd in een volgende sectie van dit hoofdstuk.,

obligaties uitgegeven met Disconto

een andere manier om dit probleem te benaderen is om op te merken dat de totale financieringskosten worden verhoogd met de discontovoet van $7.722, omdat meer op de vervaldag moet worden afgelost dan aanvankelijk werd geleend. Daarom wordt de periodieke rentebetaling van $ 4.000 verhoogd met $ 772,20 van discount amortisatie elke periode ($7,722 discount geamortiseerd op een rechte lijn basis over de 10 perioden), het produceren van periodieke rentelasten die $4,772.20 bedragen.

net als obligatiepremies worden ook disagio ‘ s in een aparte rekening opgenomen., De volgende post is nodig om de initiële obligatie-uitgifte te registreren:

de volgende posten weerspiegelen periodieke rente en aflossing op de vervaldag:

bestudeer deze illustratie zorgvuldig en merk op dat de korting op te betalen obligaties is vastgesteld op $7.722, vervolgens verminderd met $772,20 op elke Rentedatum, waardoor het eindsaldo op de vervaldag op nul komt., Op een bepaalde datum van de jaarrekening worden betaalbaar gestelde obligaties op de balans gerapporteerd als een verplichting, samen met de niet-gecorrigeerde disagio die wordt afgetrokken (bekend als een “tegenrekening”). Onderstaande afbeelding toont de balans per 30 juni 20X3. Merk op dat de unamortized korting op deze datum wordt bepaald door berekeningen geopenbaard in de tabel die volgt op:

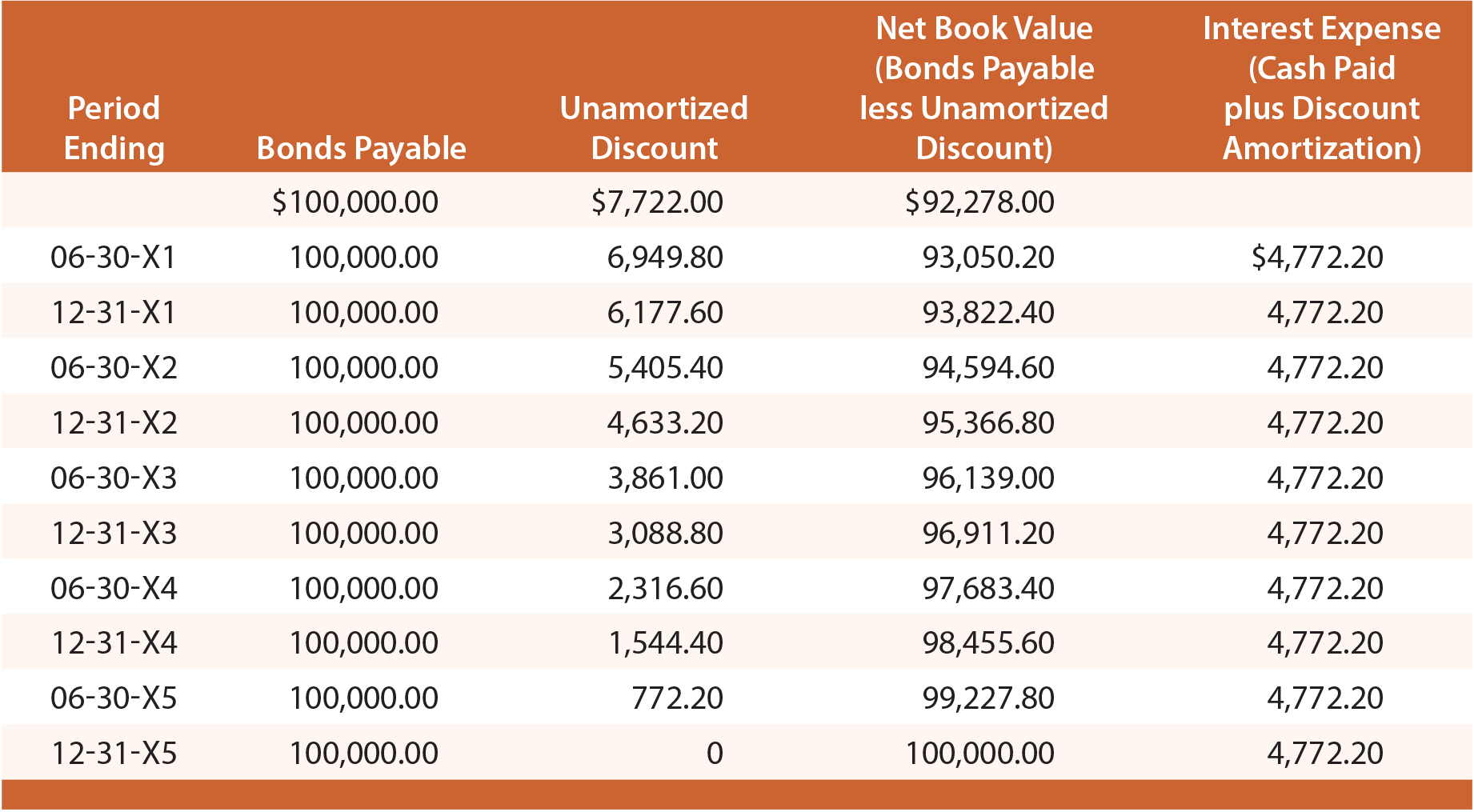
Elke jaarlijkse winst-en verliesrekening zou zijn $9,544.40 van de rentelasten ($4,772.20 X 2)., De lineaire benadering lijdt aan dezelfde beperkingen die eerder zijn besproken en is alleen aanvaardbaar als de resultaten niet wezenlijk verschillen van de resultaten die met de effective-interest-techniek worden verkregen.