- Testo
- Problemi
- il Raggiungimento degli Obiettivi
- Riempire gli Spazi vuoti
- Scelta Multipla
- Glossario
Un bond da pagare è solo una promessa di pagamento di una serie di pagamenti nel corso del tempo (la componente di interesse) e un importo fisso a scadenza (il valore nominale). Così, si tratta di una miscela di una rendita (l’interesse) e il pagamento forfettario (il volto)., Per determinare l’importo che un investitore pagherà per un’obbligazione, pertanto, richiede calcoli del valore attuale per determinare il valore corrente dei pagamenti futuri. Supponiamo che Schultz Società emette 5 anni, 8% obbligazioni. Obbligazioni hanno spesso un valore nominale di $1.000 e pagare gli interessi ogni sei mesi., Utilizzando queste ipotesi, considerare i seguenti tre scenari alternativi:



La seguente tabella mostra i calcoli del prezzo delle obbligazioni in scenari diversi:
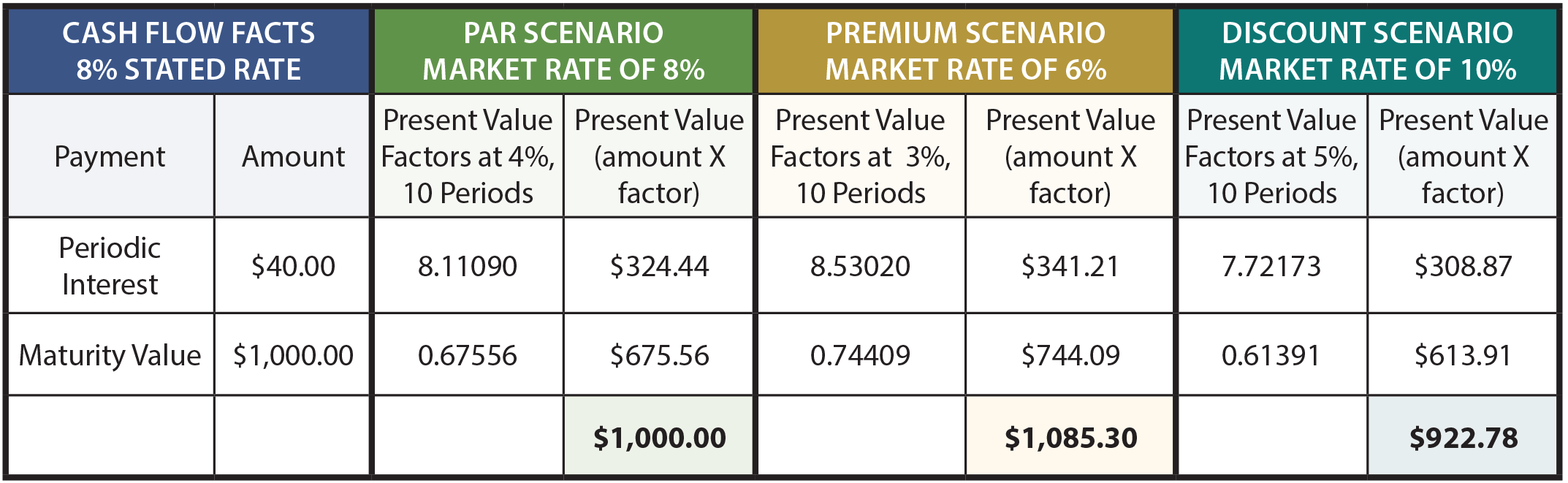
Per spiegare ulteriormente, l’importo degli interessi sui 1.000$, 8% bond è di 40 dollari ogni sei mesi. Poiché le obbligazioni hanno una vita di 5 anni, ci sono 10 pagamenti di interessi (o periodi)., L’interesse periodico è una rendita con una durata di 10 periodi, mentre il valore della scadenza è un pagamento forfettario alla fine del decimo periodo. Il tasso di interesse di mercato dell ‘ 8% equivale a un tasso semestrale del 4%, lo scenario del tasso di mercato del 6% equivale a un tasso semestrale del 3% e il tasso del 10% è del 5% per semestre.
I fattori del valore attuale sono presi dalle tabelle del valore attuale (rispettivamente rendita e somma forfettaria). Prenditi del tempo per verificare i fattori facendo riferimento alle tabelle, ai fogli di calcolo o alla routine della calcolatrice appropriati., I fattori del valore attuale vengono moltiplicati per gli importi di pagamento e la somma del valore attuale delle componenti equivale al prezzo dell’obbligazione in ciascuno dei tre scenari.
Questi calcoli non sono solo corretti teoricamente, ma sono strumenti finanziari molto accurati. Tuttavia, un punto è degno di nota. Il prezzo delle obbligazioni è spesso al 1/32nd più vicino. Cioè, un’obbligazione potrebbe essere scambiata a 103.08. Si potrebbe facilmente fraintendere questo prezzo come $1,030.80. Ma in realtà significa 103 e 8/32. In dollari, questo ammonterebbe a $1,032.50 ($1,000 X 103.25)., Avendo imparato la meccanica finanziaria delle obbligazioni, è giunto il momento di esaminare la contabilità corretta.
Obbligazioni Emesse Alla pari
Se Schultz emessi 100 di 5 anni, 8% obbligazioni alla pari, le seguenti voci sarebbe necessario :

Obbligazioni Emesse Ad Un Premio
Un modo semplice per capire obbligazioni emesse ad un premio è vista la contabilità relativa a contare i soldi!, Se Schultz emette 100 del 8%, obbligazioni a 5 anni quando il tasso di interesse di mercato è solo il 6%, poi il denaro ricevuto è di $108.530 (vedere i calcoli precedenti). Schultz dovrà rimborsare un totale di $140.000 ($4.000 ogni 6 mesi per 5 anni, più $100.000 alla scadenza).
Così, Schultz rimborserà $31.470 in più di quanto è stato preso in prestito ($140.000 – $108.530)., Questo $31.470 deve essere spesato per tutta la durata del legame; uniformemente diffondendo il periods 31.470 su 10 periodi di sei mesi produce interessi passivi periodici di $3.147 (da non confondere con l’effettivo pagamento in contanti periodico di $4.000).
Un altro modo per illustrare questo problema è notare che il costo totale del prestito è ridotto del premio di 8 8,530, poiché meno deve essere rimborsato alla scadenza di quanto è stato preso in prestito in anticipo., Pertanto, il pagamento degli interessi periodici di $4,000 viene ridotto di 8 853 dell’ammortamento del premio per ciascun periodo (premium 8,530 premio ammortizzato su base lineare nei periodi 10), producendo anche la spesa per interessi periodica di $3,147 ($4,000 – $853).
Questo argomento è intrinsecamente confuso e le voci del diario stanno effettivamente chiarendo. Si noti che il premio sulle obbligazioni pagabili è riportato in un conto separato (a differenza della contabilizzazione degli investimenti in obbligazioni coperti in un capitolo precedente, dove il premio era semplicemente incluso nel conto degli investimenti in obbligazioni).,

Studia la seguente illustrazione e osserva che il Premio sulle obbligazioni da pagare è stabilito a $8,530, poi ridotto di $853 ogni data di interesse, portando il saldo finale a zero alla scadenza.
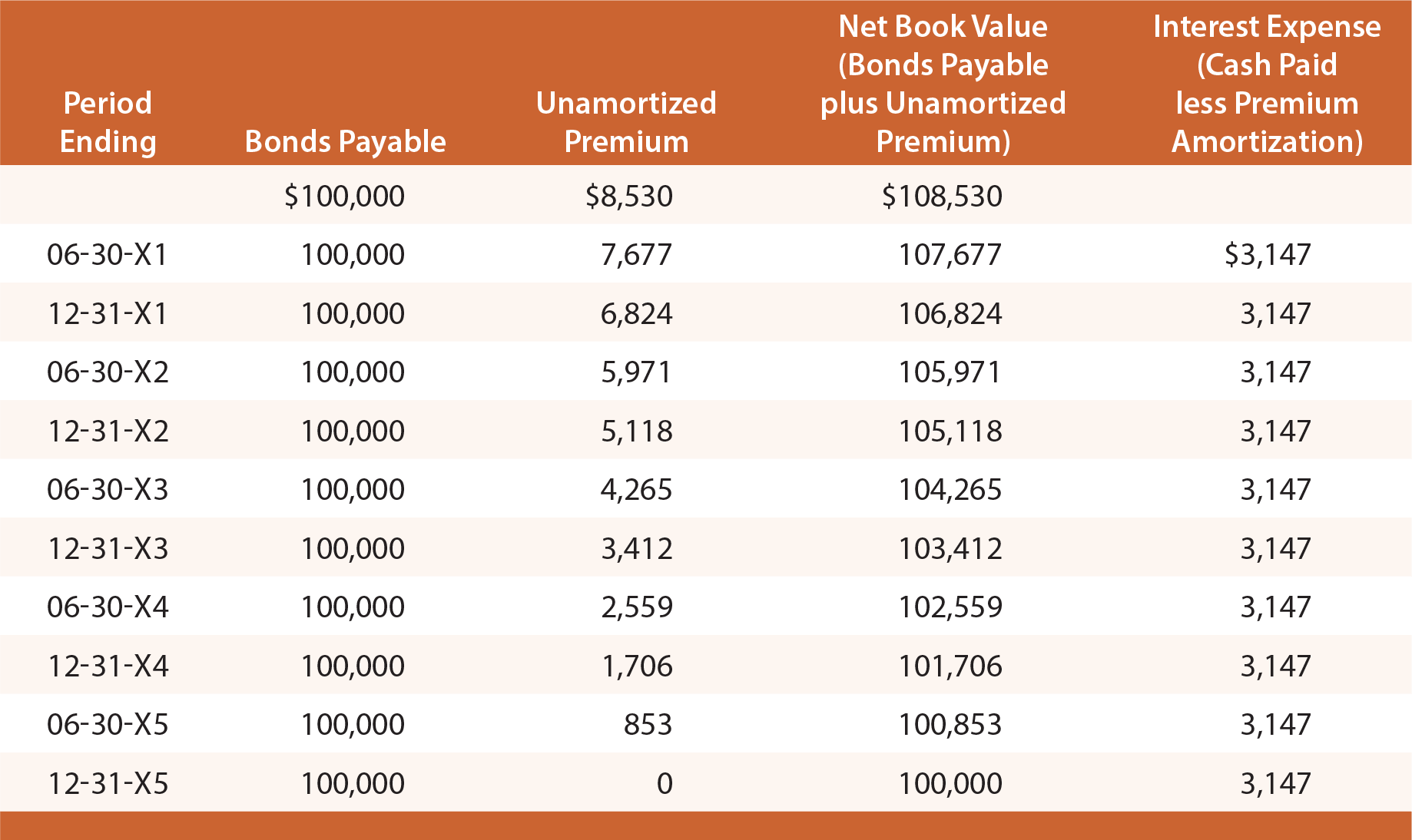
In una data data di bilancio, le obbligazioni da pagare sono segnalate in bilancio come passività, insieme al saldo del Premio non ammortizzato (noto come conto “aggiuntivo”)., Per illustrare, le informazioni di bilancio apparirebbero come segue il 31 dicembre 20X3 e 20X4:


Il conto economico per tutti i 20X3 includerebbe $6.294 di interessi passivi ($3.147 X 2). Questo metodo di contabilizzazione delle obbligazioni è noto come metodo di ammortamento lineare, poiché gli interessi passivi sono riconosciuti uniformemente per tutta la durata del legame. Anche se semplice, ha una lacuna concettuale., Si noti che la spesa per interessi è la stessa ogni anno, anche se il valore contabile netto del legame (legame più premio rimanente) è in calo ogni anno a causa di ammortamento.
Di conseguenza, la spesa per interessi ogni anno non è esattamente uguale al tasso di interesse effettivo (6%) implicito nel prezzo delle obbligazioni. Per 20X1, gli interessi passivi possono essere visti come circa il 5,8% della passività obbligazionaria (expense 6.294 spese divise per passività di inizio anno di$108.530). Per 20X4, la spesa per interessi è di circa 6.,1% (expense 6.294 spesa divisa per passività di inizio anno di $103.412).
I contabili hanno messo a punto un approccio più preciso per tenere conto delle emissioni obbligazionarie chiamato metodo dell’interesse effettivo. Essere consapevoli del fatto che il metodo di interesse effettivo più teoricamente corretto è in realtà il metodo richiesto, tranne nei casi in cui i risultati in linea retta non differiscono materialmente. Le tecniche di interesse efficace sono introdotte in una sezione seguente di questo capitolo.,
Obbligazioni emesse a sconto
Un altro modo per considerare questo problema è notare che il costo totale del prestito è aumentato dello sconto di $7,722, poiché alla scadenza deve essere rimborsato più di quanto inizialmente preso in prestito. Pertanto, il pagamento di interessi periodici periodic 4,000 è aumentato di $772.20 di ammortamento di sconto ogni periodo (discount 7,722 sconto ammortizzato su base lineare nei periodi 10), producendo interessi passivi periodici che ammontano a tot 4,772.20.
Come i premi obbligazionari, anche gli sconti sono riportati in un conto separato., La voce seguente è necessario per la registrazione iniziale di emissione di obbligazioni:

Le seguenti voci riflettere periodici di interessi e il rimborso a scadenza:

studiare Attentamente questa illustrazione, e osservare che il Sconto su Obbligazioni da pagare è fissato a $7,722, poi ridotto da $772.20 su ogni interesse oggi, portando il saldo a zero alla scadenza., In una data data di rendiconto finanziario, le obbligazioni da pagare sono segnalate sullo stato patrimoniale come passività, insieme allo sconto non ammortizzato che viene sottratto (noto come conto “contra”). L’illustrazione seguente mostra l’informativa di bilancio al 30 giugno 20X3. Si noti che lo sconto non ammortizzato in questa data è determinato dai calcoli rivelati nella tabella seguente:

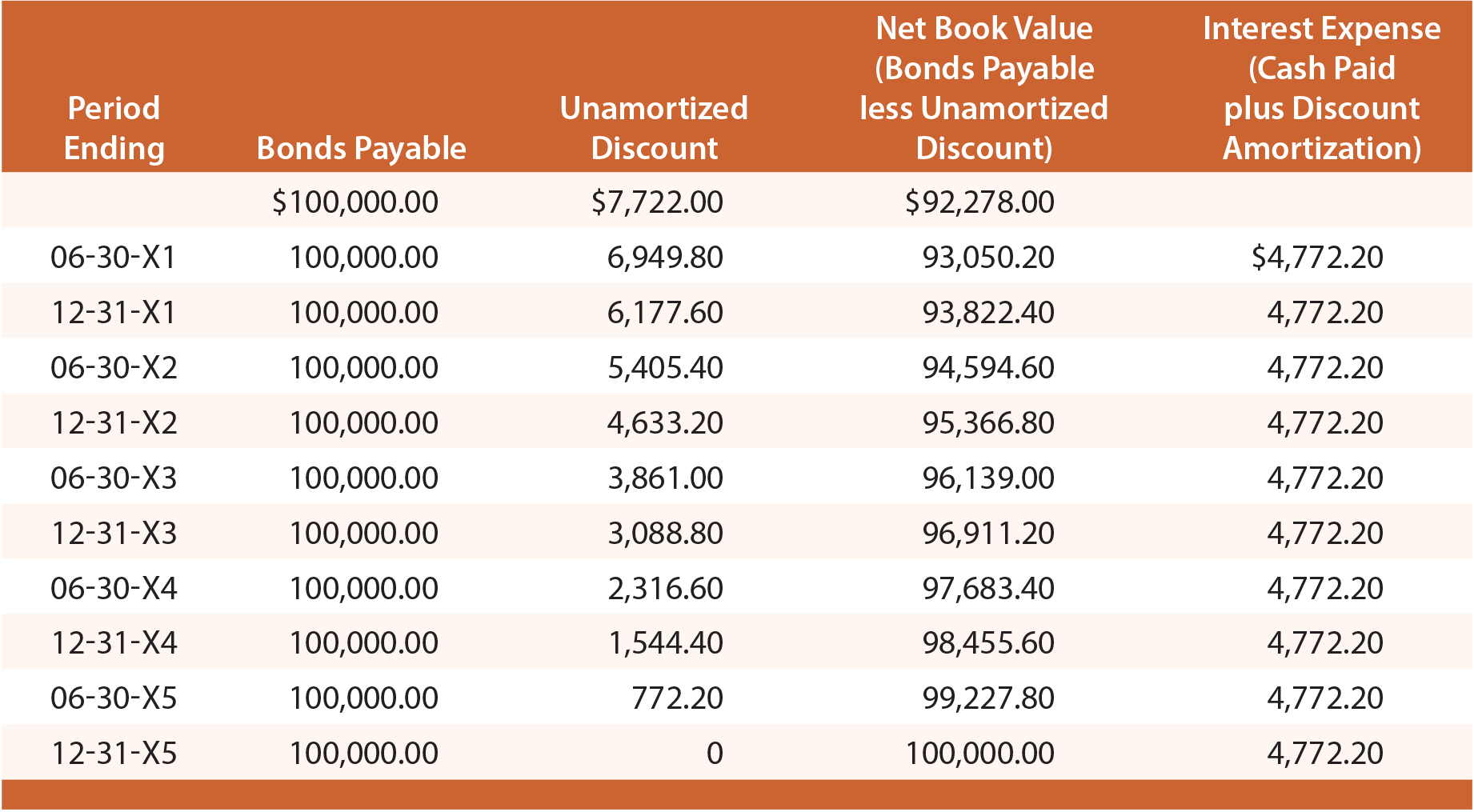
Ogni conto economico annuale includerebbe $9,544.40 di interessi passivi ($4,772.20 X 2)., L’approccio lineare soffre delle stesse limitazioni discusse in precedenza ed è accettabile solo se i risultati non sono materialmente diversi da quelli risultanti con la tecnica di interesse efficace.
Quali fattori avranno generalmente un impatto sul prezzo di emissione di un’obbligazione?
Capire perché il valore attuale è importante per i calcoli dei prezzi delle obbligazioni.
Essere in grado di calcolare il prezzo di emissione per un’obbligazione.
Preparare le voci di diario per l’intero ciclo di vita di un’obbligazione emessa alla pari.,
Essere in grado di descrivere quando un’obbligazione viene emessa a un premio e preparare le voci del diario per la sua emissione.
Utilizzare il metodo straight-line per tenere conto di un’obbligazione emessa ad un premio.
Essere in grado di descrivere quando un’obbligazione viene emessa con uno sconto e preparare le voci del diario per la sua emissione.
Utilizzare il metodo straight-line per tenere conto di un’obbligazione emessa con uno sconto.
Capire come le obbligazioni sono presentati in un bilancio, se emessi alla pari, un premio, o sconto.