- Texto
- Problemas
- logro de Objetivos
- rellene los espacios en blanco
- opción múltiple
- Glosario
solo una promesa de pagar una serie de pagos a lo largo del tiempo (el componente de interés) y una cantidad fija al vencimiento (la cantidad nominal). Por lo tanto, es una mezcla de una anualidad (el interés) y el pago de una suma global (la cara)., Para determinar la cantidad que un inversionista pagará por un bono, por lo tanto, requiere cálculos de valor presente para determinar el valor actual de los pagos futuros. Supongamos que la compañía Schultz emite bonos a 5 años, 8%. Los bonos con frecuencia tienen un valor nominal de 1 1,000 y pagan intereses cada seis meses., Usando estos supuestos, considere los siguientes tres escenarios alternativos:



la siguiente tabla muestra los cálculos del precio del bono en diferentes escenarios:
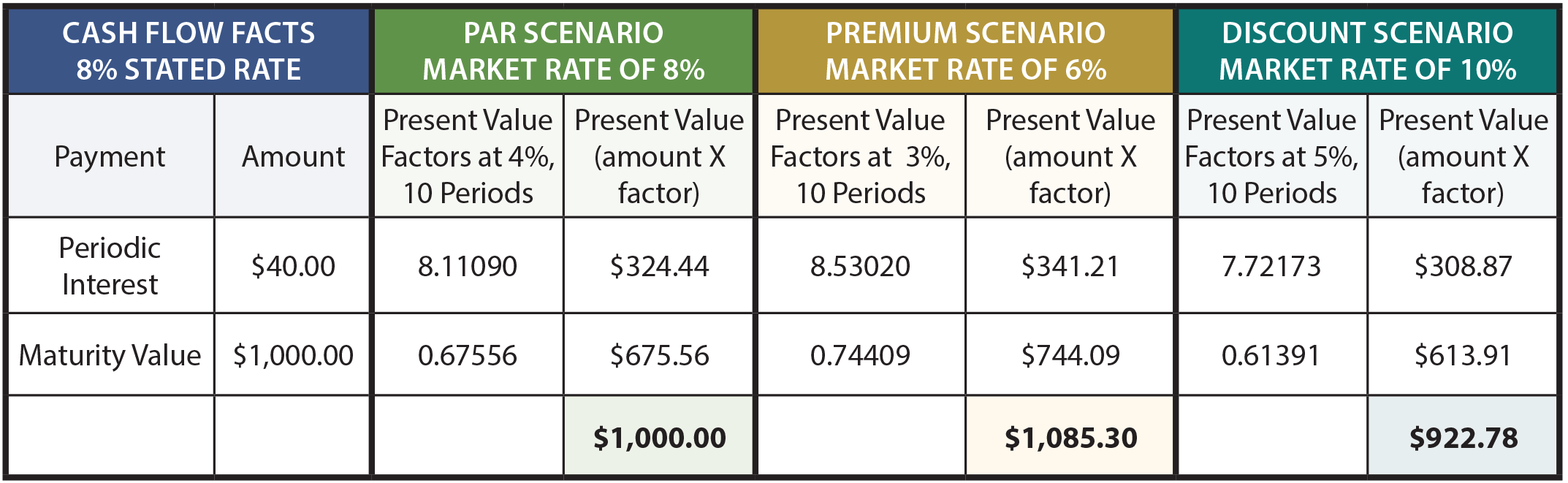
para explicar mejor, el monto del interés en el bono de 8 1,000, 8% es de 4 40 cada seis meses. Debido a que los bonos tienen una vida de 5 años, hay 10 pagos de intereses (o períodos)., El interés periódico es una anualidad con una duración de 10 períodos, mientras que el valor de vencimiento es un pago único al final del décimo período. La tasa de interés de mercado del 8% equivale a una tasa semestral del 4%, El escenario de tasa de mercado del 6% equivale a una tasa semestral del 3%, y la tasa del 10% es del 5% por período semestral.
los factores de valor presente se toman de las tablas de valor presente (anualidad y suma global, respectivamente). Tómese el tiempo para verificar los factores por referencia a las tablas apropiadas, hoja de cálculo o rutina de la calculadora., Los factores de valor actual se multiplican por las cantidades de pago, y la suma del valor actual de los componentes equivaldría al precio del bono en cada uno de los tres escenarios.
estos cálculos no solo son correctos teóricamente, sino que son herramientas financieras muy precisas. Sin embargo, un punto es digno de mención. El precio de los bonos es con frecuencia al 1/32 más cercano. Es decir, un bono podría cotizar a 103.08. Uno podría fácilmente malinterpretar este precio como $1,030.80. Pero, en realidad significa 103 y 8/32. En dólares, esto equivaldría a $1,032.50 ($1,000 X 103.25)., Habiendo aprendido la mecánica financiera de los bonos, ahora es el momento de examinar la contabilidad correcta.
bonos emitidos a la Par
Si Schultz emitió 100 de sus bonos a 5 años, 8% a la par, se requerirían las siguientes entradas :

bonos emitidos a Prima
una forma sencilla de entender los bonos emitidos a una prima es ver la contabilidad relativa al Conteo de dinero!, Si Schultz emite 100 de los bonos del 8% a 5 años cuando la tasa de interés del mercado es solo del 6%, entonces el efectivo recibido es de $108,530 (ver los cálculos anteriores). Schultz tendrá que pagar un total de $140,000 (4 4,000 cada 6 meses durante 5 años, más 1 100,000 al vencimiento).
por lo tanto, Schultz pagará 3 31,470 más de lo que se tomó prestado ($140,000 – $108,530)., Estos 3 31,470 deben gastarse a lo largo de la vida del bono; repartir uniformemente los 3 31,470 en 10 períodos de seis meses produce un gasto de interés periódico de 3 3,147 (no debe confundirse con el pago periódico en efectivo de actual 4,000).
otra forma de ilustrar este problema es observar que el costo total del préstamo se reduce en la prima de 8 8,530, ya que se debe reembolsar menos al vencimiento de lo que se tomó prestado por adelantado., Por lo tanto, el pago de intereses periódicos de 4 4,000 se reduce en premium 853 de amortización de primas cada período (premium 8,530 prima amortizada en línea recta durante los 10 períodos), también produciendo el gasto de intereses periódicos de $3,147 ($4,000 – $853).
este tema es inherentemente confuso, y las entradas del diario en realidad están aclarando. Nótese que la prima sobre los bonos pagaderos se lleva en una cuenta separada (a diferencia de la contabilidad de las inversiones en Bonos cubiertos en un capítulo anterior, donde la prima se incluyó simplemente con la cuenta de inversión en Bonos).,

estudie la siguiente ilustración y observe que la prima de los bonos pagaderos se establece en 8 8,530, luego se reduce en 8 853 cada fecha de interés, lo que lleva el saldo final a cero al vencimiento.
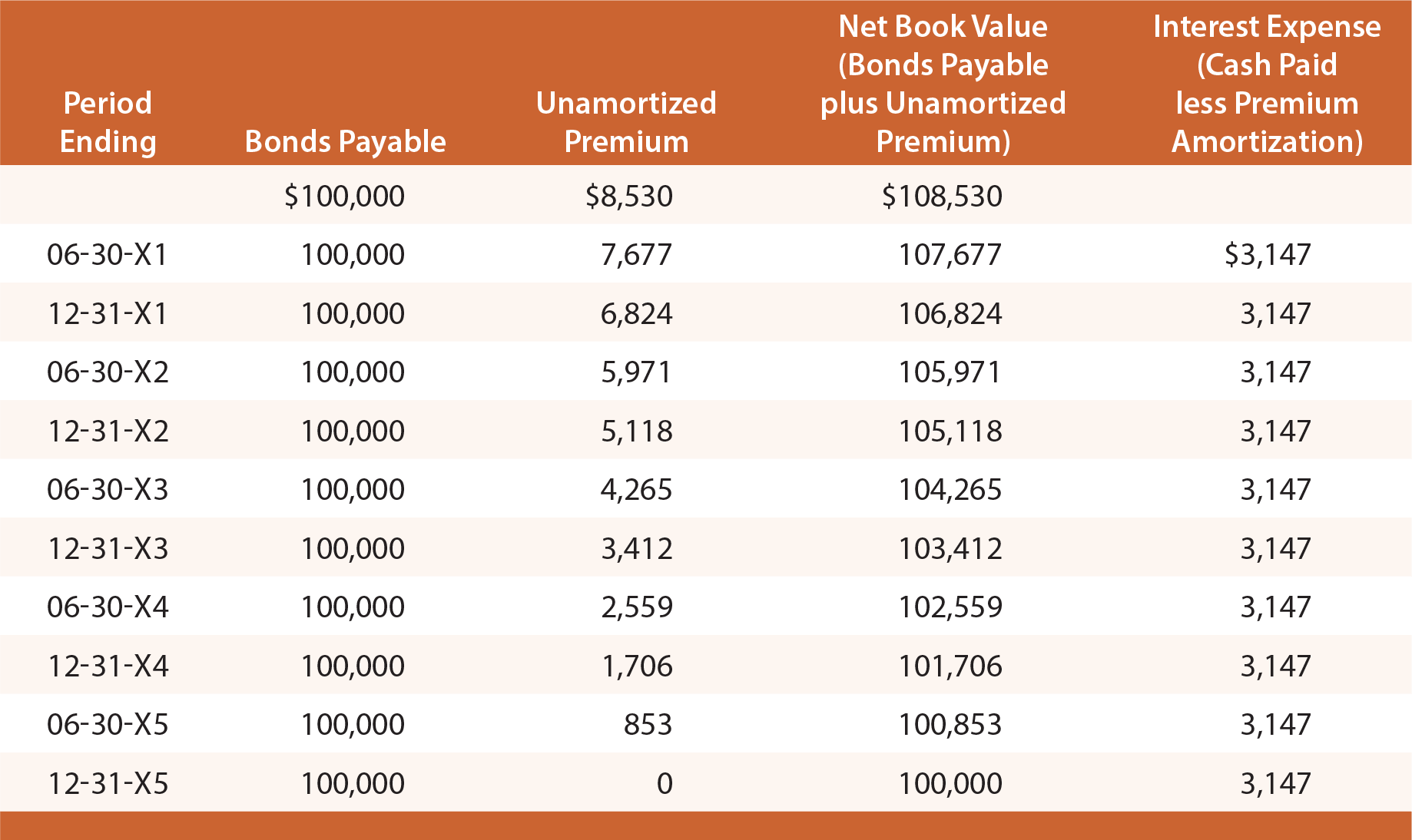
en una fecha determinada de los estados financieros, los bonos por pagar se consignan en el balance como pasivo, junto con el saldo de la prima sin amortizar (conocido como cuenta «adjunta»)., Para ilustrar, las revelaciones del balance aparecerían como sigue el 31 de diciembre, 20×3 y 20×4:


la cuenta de resultados para todo 20X3 incluiría $6,294 de gastos por intereses (3 3,147 X 2). Este método de contabilización de los bonos se conoce como método de amortización lineal, ya que el gasto por intereses se reconoce uniformemente durante la vida del bono. Aunque simple, tiene un defecto conceptual., Tenga en cuenta que el gasto por intereses es el mismo cada año, a pesar de que el valor contable neto del bono (Bono Más prima restante) está disminuyendo cada año debido a la amortización.
como resultado, el gasto por intereses cada año no es exactamente igual a la tasa de interés efectiva (6%) que estaba implícita en el precio de los bonos. Para 20X1, se puede ver que el gasto por intereses es aproximadamente el 5.8% del pasivo del bono (expense 6,294 gastos divididos por el pasivo al comienzo del año de 1 108,530). Para 20X4, el gasto por intereses es aproximadamente 6.,1% (gasto de 6 6,294 dividido por el pasivo al comienzo del año de 1 103,412).
los contables han ideado un enfoque más preciso para contabilizar las emisiones de bonos llamado método de interés efectivo. Tenga en cuenta que el método de interés efectivo más correcto teóricamente es en realidad el método requerido, excepto en aquellos casos en que los resultados en línea recta no difieren materialmente. Las técnicas de interés efectivo se presentan en una sección siguiente de este capítulo.,
bonos emitidos con descuento
otra forma de considerar este problema es tener en cuenta que el costo total del préstamo se incrementa en el descuento de 7 7,722, ya que se debe reembolsar más al vencimiento de lo que se tomó prestado inicialmente. Por lo tanto, el pago de intereses periódicos de 4 4,000 se incrementa en 7 772.20 de amortización de descuento en cada período (discount 7,722 de descuento amortizado en línea recta durante los 10 períodos), produciendo un gasto de intereses periódicos que asciende a 4 4,772.20.
al igual que las primas de bonos, Los descuentos también se llevan en una cuenta separada., Se necesita la siguiente entrada para registrar la emisión inicial de bonos:

las siguientes entradas reflejan los intereses periódicos y el reembolso al vencimiento:

estudie cuidadosamente esta ilustración y observe que el descuento on bonds payable se establece en 7 7,722, luego se reduce en 7 772.20 en cada fecha de interés, llevando el saldo final a cero al vencimiento., En una fecha determinada de los estados financieros, los bonos pagaderos se consignan en el balance como pasivo, junto con el descuento no amortizado que se resta (conocido como cuenta «contra»). La siguiente ilustración muestra la divulgación del balance al 30 de junio de 20×3. Tenga en cuenta que el descuento no amortizado en esta fecha se determina mediante cálculos revelado en la tabla que sigue:

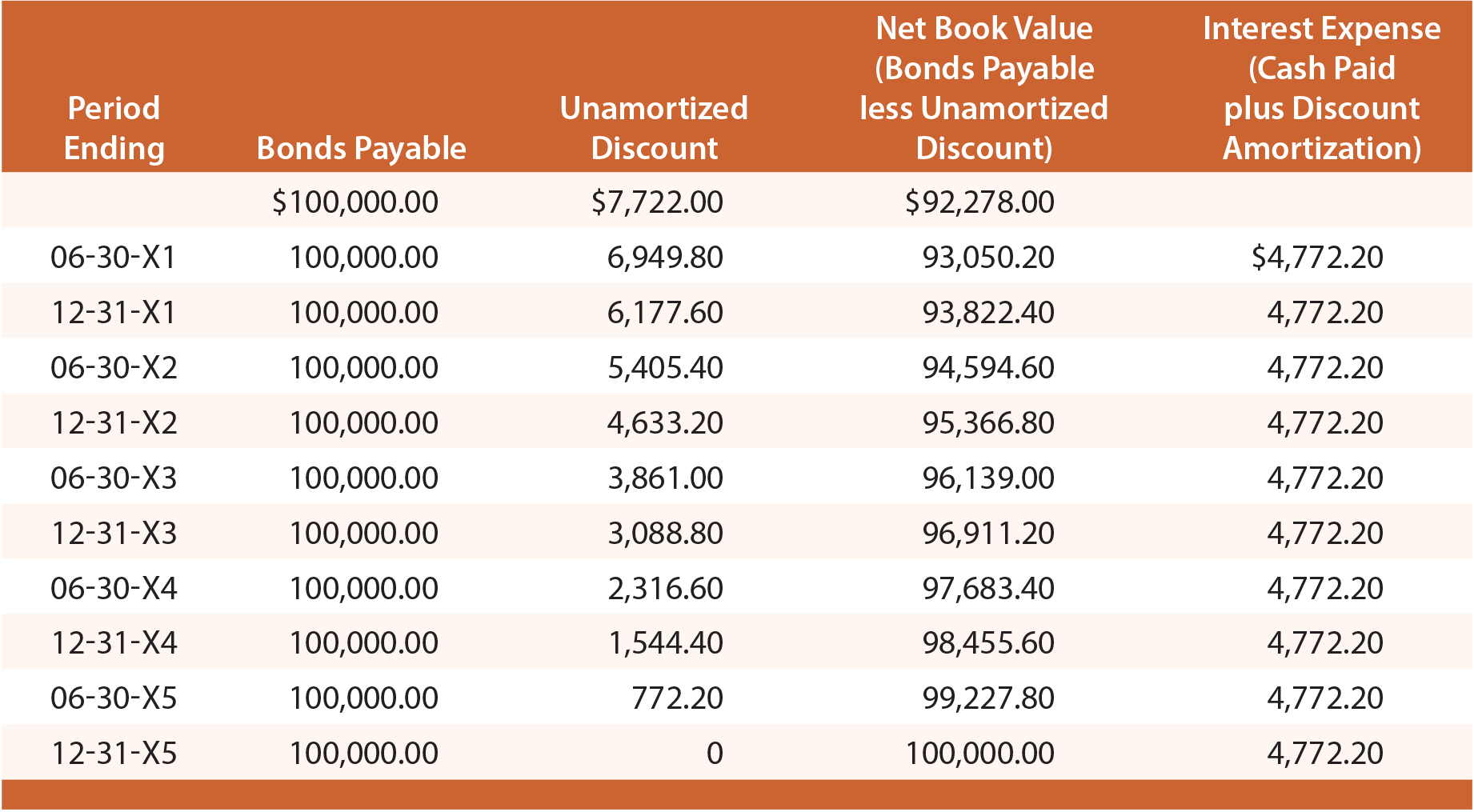
Cada uno de los ingresos anuales de instrucción incluyen $9,544.40 de gastos por intereses ($4,772.20 X 2)., El enfoque de línea recta adolece de las mismas limitaciones discutidas anteriormente, y solo es aceptable si los resultados no son materialmente diferentes de los resultantes con la técnica de interés efectivo.
¿Qué factores afectarán generalmente el precio de emisión de un bono?
entender por qué el valor presente es importante para los cálculos de precios de bonos.
Ser capaz de calcular el precio de emisión de un bono.
preparar Anotaciones en el diario para todo el ciclo de vida de un bono emitido a la par.,
ser capaz de describir cuándo se emite un bono con una prima, y preparar los asientos del diario para su emisión.
utilice el método lineal para contabilizar un bono emitido a prima.
ser capaz de describir cuándo se emite un bono con descuento y preparar asientos en el diario para su emisión.
utilice el método lineal para contabilizar un bono emitido con descuento.
entender cómo se presentan los bonos en un balance, ya sea que se emitan a la par, una prima o un descuento.