Moment de Inerție, Forma Generală
Din momentul de inerție al unui obiect obișnuit implică o distribuție continuă de masă la care variază în mod continuu distanța față de orice axă de rotație, calculul momentelor de inerție implică, în general, de calcul, disciplina de matematică care se pot ocupa de astfel de variabile continue., Din momentul de inerție al unui punct de masă este definită de
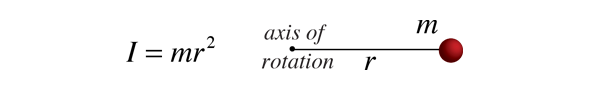
atunci momentul de inerție contribuție de un infinitesmal masa elementului dm are aceeași formă. Acest tip de masă de element se numește element diferențial de masa și momentul de inerție este dat de

Rețineți că diferențial element de momentul de inerție dI trebuie întotdeauna să fie definită în raport cu o anumită axă de rotație., Suma peste toate aceste elemente de masă se numește integrală peste masă.
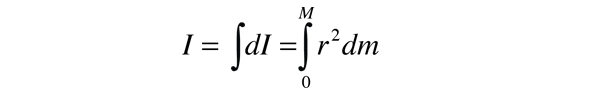
de Obicei, masa elementului dm va fi exprimat în termeni de geometria obiectului, astfel încât integrarea pot fi efectuate asupra obiectului ca un întreg (de exemplu, peste un timp uniform rod).
după ce a numit aceasta o formă generală, este probabil potrivit să subliniem că este o formă generală numai pentru axe care pot fi numite „axe principale”, un termen care include toate axele de simetrie ale obiectelor., Conceptul de moment de inerție pentru obiectele generale despre axele arbitrare este un subiect mult mai complicat. Momentul de inerție în astfel de cazuri ia forma unei cantități de tensor matematic care necesită nouă componente pentru ao defini complet.
| Exemple de integrare pentru a obține momentul de inerție. | tijă Drept |
| Cilindru | |
| Sferă |