Momento de Inércia, de Forma Geral
Desde o momento de inércia de um objeto ordinário envolve uma distribuição contínua de massa em um, continuamente, variando a distância a partir de qualquer eixo de rotação, o cálculo dos momentos de inércia implica, em geral, o cálculo, a disciplina de matemática, que pode manipular as variáveis contínuas., Desde o momento de inércia de um ponto de massa é definido pela tag
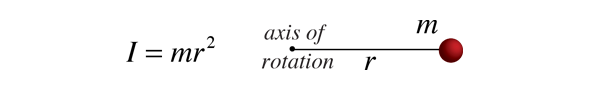
em seguida, o momento de inércia de contribuição por um infinitesmal elemento de massa dm tem a mesma forma. Este tipo de elemento de massa é chamado de um elemento diferencial de massa e o seu momento de inércia é dado por

Note que o elemento diferencial de momento de inércia dI deve ser sempre definido em relação a um determinado eixo de rotação., A soma sobre todos estes elementos de massa é chamada de integral sobre a massa.
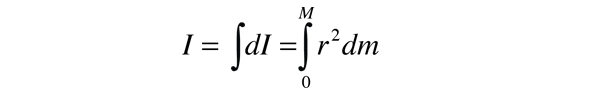
Normalmente, o elemento de massa dm será expressa em termos da geometria do objeto, de forma que a integração pode ser realizada sobre o objeto como um todo (por exemplo, através de uma longa e uniforme a haste).
tendo chamado isso de uma forma geral, é provavelmente apropriado salientar que é uma forma geral apenas para eixos que podem ser chamados de “eixos principais”, um termo que inclui todos os eixos de simetria de objetos., O conceito de momento de inércia para objetos gerais sobre eixos arbitrários é um assunto muito mais complicado. O momento de inércia em tais casos assume a forma de uma quantidade tensorial matemática que requer nove componentes para defini-la completamente.
| Exemplos de integração para obter o momento de inércia. | linha Reta de haste |
| Cilindro | |
| Esfera |