Moment bezwładności, forma Ogólna
ponieważ moment bezwładności zwykłego obiektu wiąże się z ciągłym rozkładem masy w ciągle zmieniającej się odległości od dowolnej osi obrotu, obliczanie momentów bezwładności zwykle obejmuje rachunek, dyscyplinę matematyki, która może obsługiwać takie zmienne ciągłe., Ponieważ moment bezwładności masy punktu jest zdefiniowany przez
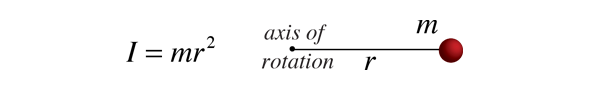
wtedy moment bezwładności elementu masy nieskończonej DM ma taką samą postać. Ten rodzaj elementu masy nazywa się różniczkowym elementem masy, a jego moment bezwładności jest podany przez

należy pamiętać, że różniczkowy element momentu bezwładności dI musi być zawsze zdefiniowany w odniesieniu do określonej osi obrotu., Suma wszystkich tych elementów masy nazywana jest całką nad masą.
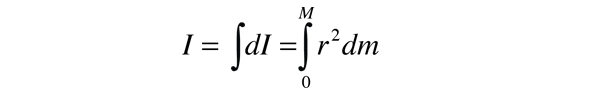
zazwyczaj element masy dm będzie wyrażony w kategoriach geometrii obiektu, tak aby integracja mogła być przeprowadzona nad obiektem jako całością (na przykład nad długim jednolitym prętem).
nazywając to formą ogólną, prawdopodobnie należy podkreślić, że jest to forma ogólna tylko dla osi, które można nazwać „głównymi osiami”, terminem obejmującym wszystkie osie symetrii obiektów., Pojęcie momentu bezwładności dla obiektów ogólnych o dowolnych osiach jest znacznie bardziej skomplikowanym tematem. Moment bezwładności w takich przypadkach przyjmuje postać matematycznej wielkości tensorowej, która wymaga dziewięciu elementów do jej pełnego zdefiniowania.
| Przykłady integracji, aby uzyskać moment bezwładności. | pręt prosty |
| Cylinder | |
| Kula |