tredimensionella former: Polyhedroner, böjda fasta ämnen och ytarea

denna sida undersöker egenskaperna hos tredimensionella eller ”fasta” former.

en tvådimensionell form har längd och bredd. En tredimensionell fast form har också djup. Tredimensionella former, av sin natur, har en insida och en utsida, åtskilda av en yta. Alla fysiska objekt, saker du kan röra, är tredimensionella.,

den här sidan täcker både straight-sidiga fasta ämnen som kallas polyhedroner, som är baserade på polygoner, och fasta ämnen med kurvor, såsom glober, cylindrar och koner.

Polyhedroner

Polyhedroner (eller polyhedra) är raka solida former. Polyhedroner är baserade på polygoner, två dimensionella planformer med raka linjer.

se våra sidegenskaper för polygoner för mer om att arbeta med polygoner.

Polyhedroner definieras som:

• raka kanter.
• platta sidor kallade ansikten.,
• hörn, kallade hörn.

Polyhedroner definieras också ofta av antalet kanter, ansikten och hörn de har, liksom om deras ansikten är alla samma form och storlek. Liksom polygoner kan polyhedroner vara regelbundna (baserade på vanliga polygoner) eller oregelbundna (baserade på oregelbundna polygoner). Polyhedroner kan också vara konkava eller konvexa.

en av de mest grundläggande och välbekanta polyhedronen är kuben. En kub är en vanlig polyhedron, med sex fyrkantiga ansikten, 12 kanter och åtta hörn.,

vanliga Polyhedroner (platoniska fasta ämnen)

de fem vanliga fasta ämnena är en speciell klass av polyhedroner, vars alla ansikten är identiska med varje ansikte som en vanlig polygon. Platoniska fasta ämnen är:

• Tetrahedron med fyra liksidiga triangelytor.
• kub med sex fyrkantiga ansikten.
• Octahedron med åtta liksidiga triangelytor.
• Dodecahedron med tolv pentagon ansikten.
• Icosahedron med tjugo liksidiga triangelytor.,

se diagrammet ovan för en illustration av var och en av dessa vanliga polyhedroner.

Vad är ett prisma?

ett prisma är någon polyhedron som har två matchande ändar och plana sidor. Om du skär ett prisma någonstans längs dess längd, parallellt med ett slut, är dess tvärsnitt detsamma – du skulle sluta med två prismor. Sidorna av ett prisma är parallellogram-fyrsidiga former med två par sidor med lika längd.

Antiprisms liknar vanliga prismor, deras ändar matchar., Men sidorna av anti-prismor består av trianglar och inte parallellogram. Antiprismer kan bli mycket komplexa.

Vad är en Pyramid?

en pyramid är en polyhedron med en polygonbas som ansluter till en apex (toppunkt) med raka sidor.

även om vi tenderar att tänka på pyramider med en fyrkantig bas, som de som de gamla egyptierna byggde, kan de faktiskt ha någon polygonbas, regelbunden eller oregelbunden. Dessutom kan en pyramid ha en spets i den direkta mitten av sin bas, en höger Pyramid, eller kan ha spetsen utanför centrum när det är en sned Pyramid.,

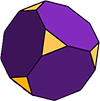
mer komplexa polyhedron

det finns många fler typer av polyhedra: symmetrisk och asymmetrisk, konkav och konvex.

arkimediska fasta ämnen består till exempel av minst två olika vanliga polygoner.

den stympade kuben (som illustrerad) är ett Arkimedeanskt solid med 14 ansikten. 6 av ansikten är vanliga oktagoner och de andra 8 är vanliga (liksidiga) trianglar. Formen har 36 kanter och 24 hörn (hörn).,

tredimensionella former med kurvor

solida former som innehåller en krökt eller rund kant är inte polyhedroner. Polyhedroner kan bara ha raka sidor.

många av objekten runt dig kommer att innehålla åtminstone några kurvor. I geometri är de vanligaste krökta fasta ämnena cylindrar, kottar, sfärer och tori (plural för torus).,

vanliga tredimensionella former med kurvor:
Cylinder	Kon
en cylinder har samma tvärsnitt från ena änden till den andra. Cylindrarna har två identiska ändar av antingen en cirkel eller en oval. Även om liknande, cylindrar är inte prismor som ett prisma har (per definition) parallellogram, platta sidor.,	en kon har en cirkulär eller oval bas och en apex (eller vertex). Sidan av konen smalnar smidigt till toppen. En kon liknar en pyramid men distinkt som en kon har en enda krökt sida och en cirkulär bas.
Sphere	Torus
formad som en boll eller en klot en sfär är ett helt runt objekt. Varje punkt på ytan av en sfär är lika långt till sfärens centrum.,	formad som en ring, ett däck eller en munk, en vanlig ring torus bildas genom att rotera en mindre cirkel runt en större cirkel. Det finns också mer komplex form av tori.

yta

vår sida om beräkning område förklarar hur man utarbetar området av tvådimensionella former och du måste förstå dessa grunder för att beräkna ytan av tredimensionella former.

För tredimensionella former talar vi om ytarea, för att undvika förvirring.,

Du kan använda dina kunskaper om området av tvådimensionella former för att beräkna ytan av en tredimensionell form, eftersom varje ansikte eller sida är effektivt en tvådimensionell form.

du arbetar därför ut området för varje ansikte och lägger sedan till dem tillsammans.

som med plana former uttrycks ytan av ett fast ämne i kvadratiska enheter: cm2, inches2, m2 och så vidare. Du hittar mer information om måttenheter på vår sida mätsystem.,

exempel på Ytberäkningar

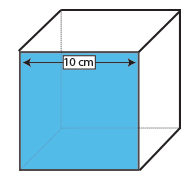
Cube

ytan på en kub är ytan på ett ansikte (längd x bredd) multiplicerat med 6, eftersom alla sex ansikten är desamma.

eftersom ansiktet på en kub är en kvadrat behöver du bara ta en mätning – längden och bredden på en kvadrat är per definition densamma.

ett ansikte av denna kub är därför 10 × 10 cm = 100cm2. Multiplicera med 6, antalet ansikten på en kub, och vi finner att ytan på denna kub är 600cm2.,

andra vanliga Polyhedroner

på samma sätt kan ytan på de andra vanliga polyhedronen (platoniska fasta ämnen) utarbetas genom att hitta området på ena sidan och sedan multiplicera svaret med det totala antalet sidor – se det grundläggande Polyhedronsdiagrammet ovan.

om området för en pentagon som utgör en dodecahedron är 22cm2 multiplicerar du detta med det totala antalet sidor (12) för att ge svaret 264cm2.,

Pyramid

för att beräkna ytan av en standard pyramid med fyra lika triangulära sidor och en fyrkantig bas:

Först träna området av basen (kvadrat) längd × bredd.

nästa träna området på ena sidan (triangel). Mät bredden längs basen och sedan höjden på triangeln (även känd som lutande längd) från den centrala punkten på basen till toppen.,

Du kan sedan antingen dela du svara med 2 för att ge dig ytan av en triangel och sedan multiplicera med 4 för att ge ytan av alla fyra sidor, eller helt enkelt multiplicera ytan av en triangel med 2.

slutligen lägga till området av basen och sidorna tillsammans för att hitta den totala ytan av pyramiden.

för att beräkna ytan av andra typer av pyramid, lägga ihop området av basen (känd som basområde) och området av sidorna (sidoområde), kan du behöva mäta sidorna individuellt.,

nätdiagram

ett geometriskt nät är ett tvådimensionellt ”mönster” för ett tredimensionellt objekt. Nät kan vara till hjälp när man arbetar ut ytan av ett tredimensionellt objekt. I diagrammet nedan kan du se hur grundläggande pyramider är konstruerade, om pyramiden är ”utfälld” du är kvar med nätet.

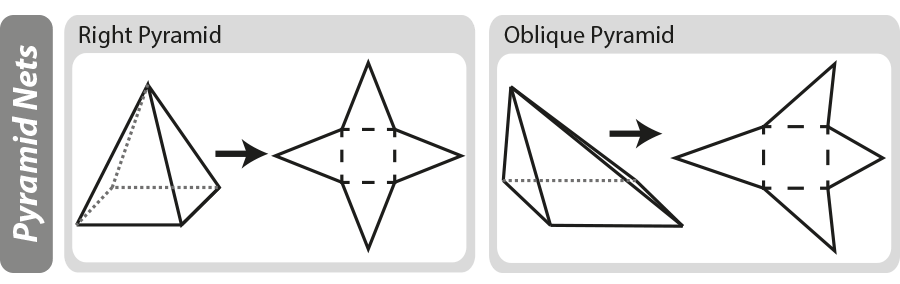
För mer information om nätdiagram se vår sida 3D former och nät.

Prisma

för att beräkna ytan av ett prisma:

prismor har två ändar samma och platta parallellogram sidor.,

beräkna området i ena änden och multiplicera med 2.

för ett vanligt prisma (där alla sidor är desamma) beräkna området på en av sidorna och multiplicera med det totala antalet sidor.

för oregelbundna prismor (med olika sidor) beräkna området på varje sida.

Lägg till dina två svar tillsammans (slutar × sidor) för att hitta prismans totala yta.,

Cylinder

för att beräkna ytan på en cylinder är det användbart att tänka på komponentdelarna i formen. Föreställ dig en burk av sockermajs – den har en topp och en botten, som båda är cirklar. Om du skär sidan längs dess längd och platta det skulle du ha en rektangel. Du måste därför hitta området med två cirklar och en rektangel.

Först träna området i en av cirklarna.

området för en cirkel är π(pi) × radius2.,

om man antar en radie på 5cm är området för en av cirklarna 3.14 × 52 = 78. 5cm2.

multiplicera svaret med 2, eftersom det finns två cirklar 157cm2

området på cylinderns sida är omkretsen av cirkeln × cylinderns höjd.

omkretsen är lika med π x 2 × radie. I vårt exempel, 3.14 × 2 × 5 = 31.4

Mät cylinderns höjd – för detta exempel är höjden 10cm. Sidoytan är 31.4 × 10 = 314cm2.,

den totala ytan kan hittas genom att lägga till området av cirklarna och sidan tillsammans:

157 + 314 = 471cm2

Kon

Vid beräkning av ytan på en kon måste du använda längden på ”snedstrecket”

’liksom radien av basen.

det är dock relativt enkelt att beräkna:

cirkelområdet vid basen av konen är, π (pi) × radius2.

i det här exemplet är summan 3.14 × 52 = 3.14 × 25 = 78.,5cm2

sidområdet, sluttande sektionen, kan hittas med hjälp av denna formel:

π(pi) × radie × längden på vinkeln.

i vårt exempel är summan 3,14 × 5 × 10 = 157cm2.

Lägg till basområdet till sidoområdet för att få konens totala yta.

78.5 + 157 = 235.5cm2

sfär

ytan på en sfär är en relativt enkel expansion av formeln för en cirkel område.

4 × π × radius2.,

för en sfär är det ofta lättare att mäta diametern – avståndet över sfären. Du kan sedan hitta radien som är hälften av diametern.

diametern på en vanlig tennisboll är 2,6 tum. Radien är därför 1,3 inches. För formeln behöver vi radien kvadrerad. 1.3 × 1.3 = 1.69.

ytan på en tennisboll är därför:

4 × 3.14 × 1.69 = 21.2264 inches2.,

Torus

för att beräkna ytan på en torus måste du hitta två radievärden.

den stora eller stora radien (R) mäts från mitten av hålet till mitten av ringen.

den lilla eller mindre radien (r) mäts från mitten av ringen till ytterkanten.

diagrammet visar två vyer av ett exempel torus och hur man mäter dess radier (eller radier).,

beräkningen för att hitta ytan är i två delar (en för varje radie). Beräkningen är densamma för varje del.

formeln är: surface area = (2NR)(2nr)

för att räkna ut ytan av exemplet torus.

(2 × π × R) = (2 × 3.14 × 20) = 125.6

(2 × π × r) = (2 × 3.14 × 4) = 25.12

multiplicera de två svaren tillsammans för att hitta den totala ytan av exemplet torus.