
en kort förklaring och bevis
Rational Root Theorem (RRT) är ett praktiskt verktyg att ha i din matematiska arsenal. Det ger och snabbt och smutsigt test för rationaliteten hos vissa uttryck. Och det hjälper till att hitta rationella rötter av polynom.,
Här är hur och varför det fungerar.,E53714″>
hur
Antag att du har ett polynom av grad n, med heltalskoefficienter:

den rationella rotteoremen Anger: om en rationell rot existerar kommer dess komponenter att dela upp de första och sista koefficienterna:

den rationella roten uttrycks i lägsta termer., Det betyder p och q delar inga gemensamma faktorer. (Det kommer att vara viktigt senare.) Täljaren delar konstanten i slutet av polynomet; demominatorn delar den ledande koefficienten.
som ett exempel:
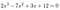
vi behöver bara titta på 2 och 12.,:
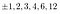
The factors of 2:
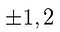
Thus, if a rational root does exist, it’s one of these:
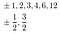
Plug each of these into the polynomial., Which one(s) — if any solve the equation? If none do, there are no rational roots.
Are any cube roots of 2 rational? A rational root, p/q must satisfy this equation.
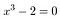
Furthermore:
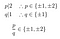
Not one of these candidates qualifies., Hoppa till:
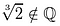
varför
Låt oss gå tillbaka till vårt paradigm polynom.,

Scoot the constant to the other side:

Now, plug in our rational root, p/q.,

multiplicera allt med q:

varje term till vänster har p gemensamt. Räkna ut det.,

det ser mycket värre ut än det behöver vara. Låt oss ersätta allt det där inom parentes med ett s. vi bryr oss inte riktigt vad som finns där inne.
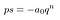
det är mycket lättare på ögonen.
Kom ihåg att p och q är heltal. De delar inte heller några gemensamma faktorer., Därför kan p inte dela med sig av sitt arbete. Div id=”ab66d6d7d5″>
täljaren delar således den konstanta termen.
gå nu tillbaka till vårt Paradigm-polynom:

den här gången är det Dålig den första termen till höger.,

Insert the rational root:

As before, multiply by qⁿ.

This time, the common factor on the left is q., Let’s extract it, and lump together the remaining sum as t.
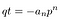
Again, q and p have no common factors. Therefore:
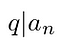
Thus proves the rational root theorem.