
Sky & teleskop
de flesta sätt att räkna och mäta saker fungerar logiskt. När det du mäter ökar blir antalet större. När du går ner i vikt, säger skalan inte ett mindre antal pund eller kilo. Men saker är inte så förnuftiga i astronomi-åtminstone inte när det gäller stjärnornas ljusheter., Ange Stjärnstorhetssystemet.
Forntida ursprung av Stellar Magnitudsystemet
Star magnitudes räknas bakåt, resultatet av en gammal fluke som verkade som en bra idé vid den tiden. Historien börjar omkring 129 f. Kr., när den grekiska astronomen Hipparchus producerade den första välkända stjärnkatalogen. Hipparchus rankade sina stjärnor på ett enkelt sätt. Han kallade de ljusaste ”av den första storleken,” helt enkelt betyder ” den största.”Stjärnor inte så ljusa han kallade” av den andra storleken ” eller näst största. De svagaste stjärnorna han kunde se han kallade ” av den sjätte magnituden.,”Omkring 140 år kopierade Claudius Ptolemy detta system i sin egen stjärnlista. Ibland lade Ptolemy till orden ”större ” eller” mindre ” för att skilja mellan stjärnor inom en storleksklass. Ptolemaios verk förblev de grundläggande astronomitexterna under de närmaste 1400 åren, så alla använde systemet med första till sjätte magnituder. Det fungerade bra.
Galileo tvingade den första ändringen. När Galileo vände sina nybyggda teleskop mot himlen upptäckte det att Stjärnor fanns som var svagare än Ptolemais sjätte storlek., ”Faktum är att med glaset kommer du att upptäcka under stjärnor av den sjätte magnituden en sådan folkmassa av andra som flyr naturlig syn att det knappast är trovärdigt”, exulterade han i sin 1610-kanal Sidereus Nuncius. ”Den största av dessa . . . vi kan utse från och med den sjunde magnituden.”Således kom en ny term in i det astronomiska språket, och stjärnstorhetssystemet blev öppet. Det kan inte finnas någon återvändo.
När teleskop blev större och bättre, fortsatte astronomer att lägga till fler magnituder till botten av skalan., Idag visar ett par 50-millimeters kikare stjärnor av ungefär 9: e magnituden, ett 6-tums amatörteleskop kommer att nå till 13: e magnituden, och rymdteleskopet Hubble har sett objekt som svaga som 31: e magnituden.
i mitten av 1800-talet insåg astronomer att det fanns ett trängande behov av att definiera hela skalan av stjärnans magnitudsystem mer exakt än genom ögonbollsdom. De hade redan bestämt att en stjärna av 1: A magnituden skiner med cirka 100 gånger ljuset från en stjärna av 6: e magnituden. Därför 1856 Oxford astronomen Norman R., Pogson föreslog att en skillnad på fem magnituder exakt definieras som ett ljusstyrkeförhållande på 100 till 1. Denna praktiska regel antogs snabbt. En magnitud motsvarar sålunda en ljushetsskillnad på exakt den femte roten av 100, eller mycket nära 2.512-ett värde som kallas Pogson-förhållandet.
det resulterande stjärnstorhetssystemet är logaritmiskt, i snyggt samförstånd med 1850s tro på att alla mänskliga sinnen är logaritmiska i sitt svar på stimuli. Decibelskalan för rating loudness gjordes också logaritmisk.,
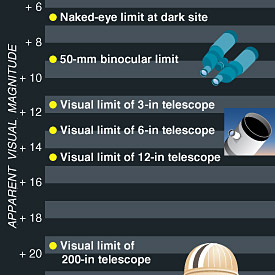
femtioåtta magnituder med tydlig ljusstyrka omfattar de saker som astronomer studerar, från den uppenbara solen till de svagaste objekt som upptäckts med Rymdteleskopet Hubble. Detta intervall motsvarar ett ljusstyrkeförhållande på cirka 200 miljarder biljoner.
Sky& teleskop
tyvärr är det inte riktigt så, inte för ljusstyrka, ljud eller något annat. Våra uppfattningar om världen följer maktlagskurvor, inte logaritmiska. Således en stjärna av magnitud 3.,0 ser faktiskt inte exakt halvvägs i ljusstyrka mellan 2.0 och 4.0. Det ser lite svagare ut än så. Stjärnan som ser halvvägs mellan 2.0 och 4.0 Kommer att vara ungefär magnitud 2.8. Ju bredare storleksgapet desto större är denna skillnad. Följaktligen använder Sky& teleskopets datorritade Sky-kartor stjärnprickar som är dimensionerade enligt en power-law-relation.
men den vetenskapliga världen på 1850-talet var gaga för logaritmer, så nu är de låsta i stellar magnitudsystemet lika fast som Hipparchus bakåtnummering.,
nu när stjärnstorngraderna rankades på en exakt matematisk skala, blev ett annat problem oundvikligt. Några” 1st-magnitude ” stjärnor var mycket ljusare än andra. Astronomer hade inget annat val än att utvidga skalan till ljusare värden såväl som svaga. Således är Rigel, Capella, Arcturus och Vega magnitud 0, ett besvärligt uttalande som låter som om de inte har någon ljusstyrka alls! Men det var för sent att börja om. Storleksskalan sträcker sig längre till negativa tal: Sirius lyser vid magnitud -1,5, Venus når -4,4, fullmånen är ca -12.,5, och solen flammar i magnitud -26.7.
andra färger, andra magnituder
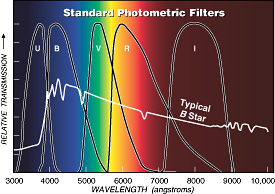
bandpasserna för standard ubvri färgfilter, tillsammans med spektrumet för en typisk blåvit stjärna.
Sky& teleskop
Vid slutet av 1800-talet använde astronomer fotografering för att spela in himlen och mäta stjärnljuset, och ett nytt problem dök upp. Vissa stjärnor som visar samma ljusstyrka i ögat visade olika ljusheter på film och vice versa., Jämfört med ögat var fotografiska emulsioner mer känsliga för blått ljus och mindre så mot rött ljus. Följaktligen utarbetades två separata skalor för stjärnans magnitudsystem. Visuell magnitud, eller mvis, beskrev hur en stjärna såg på ögat. Fotografisk magnitud, eller mpg, hänvisade till stjärnbilder på blåkänslig svartvit film. Dessa är nu förkortade MV respektive mp.
denna komplikation visade sig vara en välsignelse i förklädnad. Skillnaden mellan en stjärnas fotografiska och visuella magnitud var ett bekvämt mått på stjärnans färg., Skillnaden mellan de två typerna av storleksordning namngavs ” färgindex.”Dess värde blir allt mer positivt för gula, orange och röda stjärnor och negativt för blåa.
men olika fotografiska emulsioner har olika spektrala svar! Och människors ögon skiljer sig också. För en sak blir dina ögonlinser gula med ålder; gamla människor ser världen genom gula filter. Magnitudsystem avsedda för olika våglängdsområden måste vara tydligare definierade än detta.,
idag specificeras exakta magnituder av vad en standard fotoelektrisk fotometer ser genom standardfärgfilter. Flera fotometriska system har utarbetats; den mest kända kallas UBV efter de tre filter som oftast används. U omfattar nära ultraviolett, B är blå och V motsvarar ganska nära den gamla visuella magnituden; dess breda topp är i det gulgröna bandet, där ögat är mest känsligt.
färgindex definieras nu som b-magnituden minus v-magnituden. En ren vit stjärna har en B-V på ca 0,2, vår gula sol är 0.,63, orange-röd Betelgeuse är 1,85, och den blåaste stjärnan trodde möjligt är -0.4, ljusblå-vit.
så framgångsrik var UBV-systemet att det utökades redward med R och i-filter för att definiera standard röda och nära infraröda magnituder. Därför kallas det ibland UBVRI. Infraröda astronomer har burit det till ännu längre våglängder, plocka upp alfabetiskt efter jag att definiera J, K, L, M, N, och Q Band. Dessa valdes för att matcha våglängderna av infraröda ”fönster” i jordens atmosfär — våglängder där vattenånga inte helt absorberar stjärnljus.,
i alla vågband har den ljusa stjärnan Vega valts (godtyckligt) för att definiera magnitud 0.0. Eftersom Vega är dimmer vid infraröda våglängder än i synligt ljus, är infraröda magnituder per definition och ganska artificiellt ”ljusare” än sina visuella motsvarigheter.
utseende och verklighet
vad är då ett objekts verkliga ljusstyrka? Hur mycket total energi skickar den till oss vid alla våglängder kombinerade, synliga och osynliga? Svaret kallas den bolometriska storleken, mbol, eftersom total strålning en gång mättes med en enhet som kallas en bolometer., Den bolometriska storleken har kallats Guds ögonvy av ett objekts sanna glans. Astrofysiker värdesätter det som det verkliga måttet på ett objekts totala energiutsläpp som ses från jorden. Den bolometriska korrigeringen berättar hur mycket ljusare den bolometriska storleken är än v-magnituden. Dess värde är alltid negativt, eftersom någon stjärna eller objekt avger åtminstone viss strålning utanför den visuella delen av det elektromagnetiska spektrumet.
fram till nu har vi bara handlat med uppenbara magnituder – hur ljusa saker ser ut från jorden., Vi vet inte hur starkt ett objekt är förrän vi också tar hänsyn till avståndet. Således skapade astronomer den absoluta storleksskalan. Ett objekts absoluta magnitud är helt enkelt hur ljust det skulle visas om det placerades på ett standardavstånd på 10 parsek (32,6 ljusår).

på den vänstra kartan över Canis Major indikerar punktstorlekarna stjärnornas skenbara magnituder; prickarna matchar stjärnornas ljushet som vi ser dem., Den högra versionen anger samma stjärnors absoluta magnituder — hur ljusa de skulle visas om de alla placerades på samma avstånd (32,6 ljusår) från jorden. Absolut magnitud är ett mått på sann stellar ljusstyrka.
Sky & teleskop
sett från detta avstånd, skulle solen skina på en imponerande visuell magnitud 4,85. Rigel skulle bläsa på en bländande -8, nästan lika ljus som kvartsmånen. Den röda dvärgen Proxima Centauri, den närmaste stjärnan till solsystemet, verkar vara magnitud 15.,6, den minsta lilla glimmer synlig i ett 16-tums teleskop! Att veta absoluta magnituder gör klart hur mycket olika är de objekt som vi nonchalant klump tillsammans under det enda ordet ” stjärna.”
absoluta magnituder skrivs alltid med ett kapital M, skenbara magnituder med ett lägre fall m. någon typ av skenbar magnitud-fotografisk, bolometrisk eller vad som helst — kan omvandlas till en absolut storlek.
(för kometer och asteroider används en mycket annan ”absolut magnitud”., Standarden här är hur ljus objektet skulle se ut för en observatör som står på solen om objektet var en astronomisk enhet bort.)
så är det stellar magnitudsystemet för komplicerat? Alls. Det har vuxit och utvecklats för att fylla varje ljusstyrka-mätning behöver exakt som krävs. Hipparcus skulle bli jätteglad.