Bayes teorem finner många användningsområden i sannolikhetsteorin och statistiken. Det finns en mikro chans att du aldrig har hört talas om detta teorem i ditt liv. Visar sig att denna sats har hittat sin väg in i en värld av maskininlärning, för att bilda en av de högt dekorerade algoritmer. I den här artikeln kommer vi att lära oss allt om naiva Bayes-algoritmen, tillsammans med dess variationer för olika ändamål i maskininlärning.
som du kanske gissat kräver detta att vi ser saker ur en probabilistisk synvinkel., Precis som i maskininlärning har vi attribut, svarvariabler och förutsägelser eller klassificeringar. Med hjälp av denna algoritm kommer vi att hantera sannolikhetsfördelningen av variablerna i datauppsättningen och förutsäga sannolikheten för svarsvariabeln som tillhör ett visst värde, med tanke på attributen för en ny instans. Låt oss börja med att granska Bayes teorem.
Bayes’ sats
detta gör det möjligt för oss att undersöka sannolikheten för en händelse baserat på förkunskap om alla händelser som relaterade till den tidigare händelsen., Så till exempel, sannolikheten att priset på ett hus är hög, kan bättre bedömas om vi känner till anläggningarna runt det, jämfört med den bedömning som gjorts utan kunskap om platsen för huset. Bayes teorem gör exakt det.

ovanstående ekvation ger den grundläggande representationen av Bayes teorem., Här är A och B två händelser och,
P(A|B) : den villkorliga sannolikheten att Händelse a inträffar , med tanke på att B har inträffat. Detta är också känt som den bakre sannolikheten.
p(a) och P(b) : Sannolikhet för A och B utan hänsyn till varandra.
P(B|A) : den villkorliga sannolikheten att Händelse B inträffar , med tanke på att A har inträffat.
nu ska vi se hur det passar bra för syftet med maskininlärning.,
ta ett enkelt maskininlärningsproblem, där vi behöver lära oss vår modell från en viss uppsättning attribut(i träningsexempel) och sedan bilda en hypotes eller en relation till en svarsvariabel. Då använder vi denna relation för att förutsäga ett svar, givna attribut för en ny instans. Med hjälp av Bayes teorem är det möjligt att bygga en elev som förutsäger sannolikheten för svarvariabeln som tillhör någon klass, med tanke på en ny uppsättning attribut.
överväga den tidigare ekvationen igen. Anta nu att A är svarsvariabeln och B är inmatningsattributet., Så enligt ekvationen har vi
P(a|b) : villkorlig sannolikhet för svarsvariabel som tillhör ett visst värde, med tanke på inmatningsattributen. Detta är också känt som den bakre sannolikheten.
P(A) : den tidigare sannolikheten för svarsvariabeln.
P(b) : sannolikheten för träningsdata eller bevis.
P(B|A) : Detta kallas sannolikheten för träningsdata.,
därför kan ovanstående ekvation skrivas om som
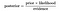
låt oss ta ett problem, där antalet attribut är lika med n och svaret är ett booleskt värde, dvs det kan vara i en av de två klasserna. Attributen är också kategoriska (2 kategorier för vårt fall). Nu, för att träna klassificeraren, måste vi beräkna P (B|A), för alla värden i instansen och svarsytan., Det betyder att vi måste beräkna 2 * (2^n -1), parametrar för att lära sig denna modell. Detta är helt klart orealistiskt i de flesta praktiska inlärningsområden. Till exempel, om det finns 30 booleska attribut, måste vi uppskatta mer än 3 miljarder parametrar.
naiv Bayes algoritm
komplexiteten i ovanstående Bayesian klassificerare måste minskas, för att det ska vara praktiskt. Den naiva Bayes algoritmen gör det genom att göra ett antagande om villkorligt oberoende över träningsdataset. Detta minskar drastiskt komplexiteten hos ovan nämnda problem till bara 2n.,
antagandet om villkorligt oberoende anger att, med tanke på slumpmässiga variabler X, Y och Z, säger Vi X är villkorligt oberoende av Y givet Z, om och endast om sannolikhetsfördelningen som styr X är oberoende av värdet av Y givet Z.
med andra ord, X och Y är villkorligt oberoende given Z om och endast om, med tanke på att Z uppstår, kunskap om huruvida X inträffar ger ingen information om sannolikheten för att Y inträffar, och kunskap om huruvida Y inträffar ger ingen information om sannolikheten för att X inträffar.,
detta antagande gör Bayes-algoritmen naiv.
givet, n olika attributvärden, sannolikheten nu kan skrivas som
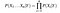
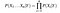
här representerar X attributen eller funktionerna, och Y är svarsvariabeln. Nu blir P (X|Y) lika med produkterna av, sannolikhetsfördelning av varje attribut X givet Y.,
maximera en Posteriori
vad vi är intresserade av, är att hitta den bakre sannolikheten eller P(Y / X). Nu, för flera värden på Y, måste vi beräkna detta uttryck för var och en av dem.
Med tanke på en ny instans Xnew måste vi beräkna sannolikheten för att Y kommer att ta på sig ett visst värde, med tanke på de observerade attributvärdena för Xnew och med tanke på fördelningarna P(Y) och P(X|Y) beräknade från träningsdata.
Så, hur kommer vi att förutsäga klassen av svarsvariabeln, baserat på de olika värden vi uppnår för P(Y|X)., Vi tar helt enkelt det mest sannolika eller maximala av dessa värden. Därför är denna procedur också känd som att maximera en posteriori.
maximera sannolikheten
om vi antar att svarsvariabeln är jämnt fördelad, är det lika sannolikt att få något svar, då kan vi ytterligare förenkla algoritmen. Med detta antagande blir priori eller P (Y) ett konstant värde, vilket är 1/kategorier av svaret.
as, priori och bevis är nu oberoende av svarsvariabeln, dessa kan tas bort från ekvationen., Därför reduceras maximeringen av posteriori för att maximera sannolikhetsproblemet.
funktionsfördelning
som framgår ovan måste vi uppskatta fördelningen av svarsvariabeln från träningsuppsättningen eller anta enhetlig fördelning. På samma sätt, för att uppskatta parametrarna för en funktions distribution, måste man anta en distribution eller generera icke-parametriska modeller för funktionerna från träningsuppsättningen. Sådana antaganden är kända som händelsemodeller. Variationerna i dessa antaganden genererar olika algoritmer för olika ändamål., För kontinuerliga distributioner är Gaussian naive Bayes den valfria algoritmen. För diskreta funktioner, multinomial och Bernoulli distributioner som populära. Detaljerad diskussion om dessa variationer är utanför tillämpningsområdet för denna artikel.
naiva Bayes klassificerare fungerar riktigt bra i komplexa situationer, trots förenklade antaganden och naivitet. Fördelen med dessa klassificerare är att de kräver ett litet antal träningsdata för att uppskatta de parametrar som är nödvändiga för klassificering. Detta är algoritmen för val för text kategorisering., Detta är den grundläggande idén bakom naiva Bayes klassificerare, att du måste börja experimentera med algoritmen.