hitta kvadratiska funktioner för givna paraboler – kvadratiska funktioner

hitta kvadratiska funktioner för givna paraboler

det finns så många olika typer av problem som du kan bli ombedd med avseende på kvadratiska ekvationer. I den här artikeln kommer fokus att läggas på hur vi kan utveckla en kvadratisk ekvation från en kvadratisk graf med ett par olika metoder., Men innan vi kommer in i dessa typer av problem, ta en stund att leka med kvadratiska uttryck på denna underbara Online grafräknare här. Ju bekvämare du är med kvadratiska grafer och uttryck, desto lättare blir det här ämnet!

låt oss nu lösa problem med denna kunskap, nämligen hur man hittar ekvationen för en parabola!

hur man hittar en kvadratisk ekvation från ett diagram:

för att hitta en kvadratisk ekvation från ett diagram finns det två enkla metoder som man kan använda: med 2 poäng eller med 3 poäng.,

1) Hitta kvadratisk ekvation från 2 poäng

för att hitta en kvadratisk ekvation från ett diagram med endast 2 poäng måste en av dessa punkter vara vertexen. Med vertexen och en annan punkt kan vi dela dessa koordinater i vad som kallas ”vertexformen” och sedan lösa för vår ekvation., Vertexformeln är som följer, där (d,f) är vertexpunkten och (x,y) är den andra punkten:

(y±d)=a(x±f)2(y \pm d) = A(x \pm f)^{2}(y±d)=a(x±f)2

Vertexform kan också skrivas i sin mer avancerade form. ”korrekt” form, som:

y=a(x±f)2 Dy = A(x \pm f)^{2} \MP Dy=A(x±f)2 d

med hjälp av denna formel är allt vi behöver göra sub i vertexen och den andra punkten, lösa för en, och sedan skriva om vår slutliga ekvation., Det bästa sättet att bli bekväm med att använda detta formulär är att göra ett exempel problem med det.

exempel:

Bestäm ekvationen för parabolen som visas i bilden nedan.

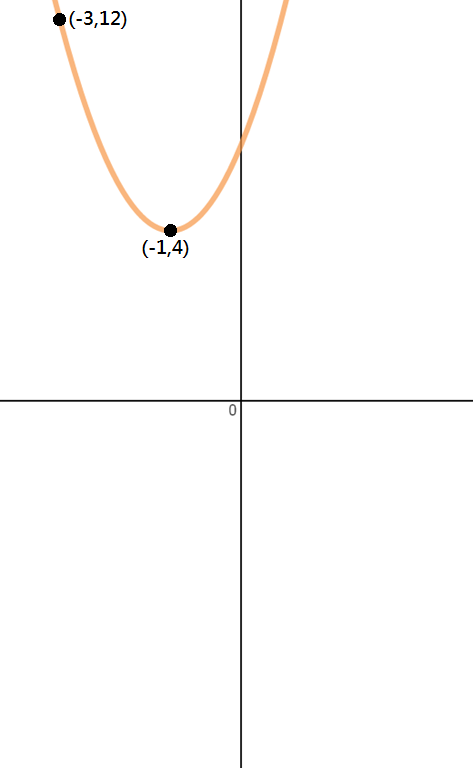
Steg 1: identifiera punkter

eftersom vi bara ges två punkter i detta problem, vertex och en annan punkt måste vi använda vertexform för att lösa detta problem.fråga.,

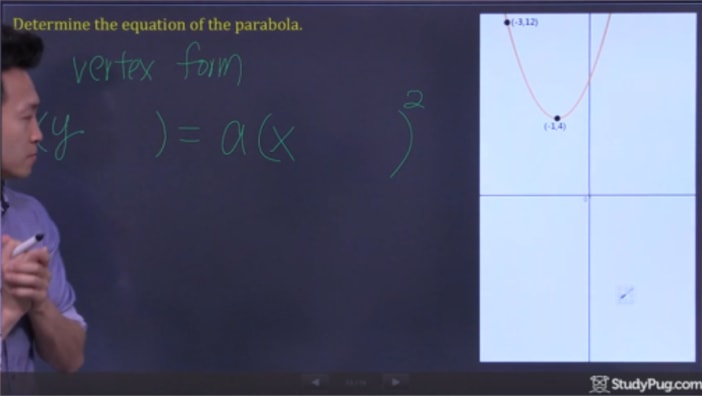
steg 2: Subpunkter i Vertexform och lösa för ”a”

nu är allt vi behöver göra sub i våra två punkter in i vertex formel och lösa för ”A” att ha all information för att skriva vår slutliga kvadratiska ekvation.,4) = a(-3+1)2(12 – 4) = a(-3 + 1)^{2}(12-4)=A(-3+1)2

8=a(-2)28 = a(-2)^{2}8=a(-2)28=4a8 = 4A8=4aA=2A = 2a=2

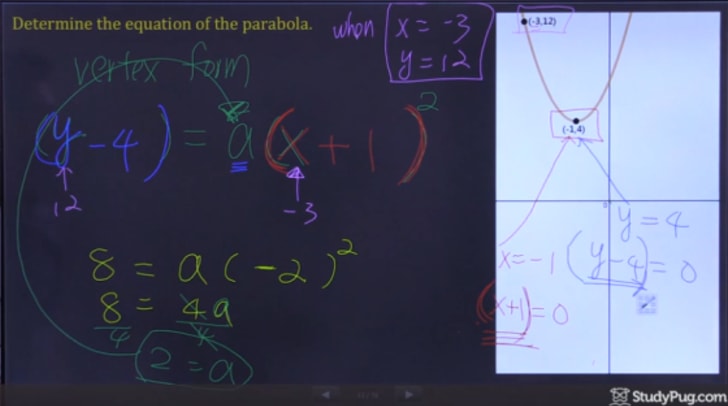
steg 3: Skriv ut kvadratisk ekvation

Efter att ha löst för ”A” har vi nu all information vi behöver för att skriva ut vårt slutliga svar.,

y−4=2(x+1)2y – 4 = 2(x + 1)^{2}y−4=2(x+1)2

och sedan, i rätt vertex form av en parabola, är vårt slutliga svar:

y=2(x+1)2+4y = 2(x + 1)^{2} + 4Y=2(x+1)2+4

som avslutar lektionen på vertexform och hur man hittar en kvadratisk ekvation från 2 poäng!, Om du vill uppdatera ditt minne om relaterade ämnen som, hur man löser kvadratiska uttryck i vertexform, hur man konverterar en vanlig kvadratisk ekvation från standardform till vertexform genom att fylla i torget och hur man använder vertexformel, se till att kolla in våra lektioner.

2) Hitta kvadratisk ekvation från 3 poäng

i vissa fall kommer vi inte att vara så lyckliga att vi får punkten på vertexen. Om så är fallet kan vi inte längre hitta det kvadratiska uttrycket med bara två punkter och behöver göra något lite annorlunda., Om vi får information om X-avlyssning av en parabola, liksom en annan punkt, kan vi hitta den kvadratiska ekvationen med hjälp av en ekvation som kallas ”factored form”. Den allmänna ekvationen för den factored formulärformeln är följande, med B och c som X-koordinatvärdena för X-avlyssningarna:

y=a(x−B)(x−c)y = a(x – B)(x – c)y=a(x−B)(x−c)

med hjälp av denna formel är allt vi behöver göra sub I x-koordinaterna av X-fångar, en annan punkt, och sedan lösa för en så att vi kan skriva ut vårt slutliga svar., Återigen är det bästa sättet att bli bekväm med denna form av kvadratiska ekvationer att göra ett exempel problem.

exempel:

Bestäm ekvationen för parabolen som visas i bilden nedan:

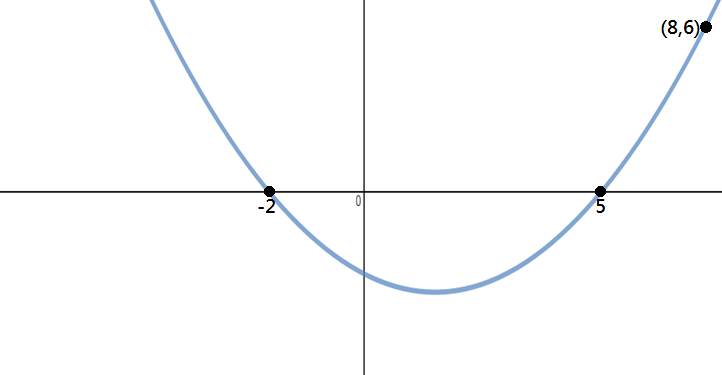
Steg 1: identifiera punkter

eftersom vi får tre punkter i detta problem, x-avlyssningarna och en annan punkt, kan vi använda faktored form för att lösa denna fråga.,

från grafen kan vi se att x-avlyssningarna är -2 och 5, och punkten på parabolen är (8,6).

steg 2: sub punkter i Vertex Form och lösa för”a ”

nu allt vi behöver göra är sub i våra värden i den factored form formel och lösa för” a ” att ha all information för att skriva vår slutliga kvadratiska ekvation.,(x – 5)y=(x+2) (x−5)

därefter kan vi använda punkten på parabolen (8,6) för att lösa för ”a”:

6=a(8+2)(8-5)6 = a(8 + 2)(8 – 5)6=A(8+2)(8-5)6=a(10)(3)6 = a(10)(3)6=a(10)(3)6=30a6 = 30Aa=15a=\frac{1}{5}a = 51

steg 3: Skriv ut kvadratisk ekvation

efter att ha löst för ”A” har vi nu all information vi behöver för att skriva ut vårt slutliga svar.,

y = 15(x+2)(x−5)y=\frac{1}{5} (x + 2)(x – 5)y=51(x+2)(x−5)

och det är allt som finns till det! Det är de två viktigaste metoderna för att hitta en kvadratisk funktion från en given parabola. För ytterligare studier av kvadratiska funktioner och deras grafer, kolla in dessa användbara videor som handlar om diskriminanten, grafera kvadratiska ojämlikheter och koniska sektioner.