Calculate Log & Antilog Online (Svenska)

Mathematical Formulas

Calculating log (logbx):

logbx = y implies by = x.,

var,

• b = bas,
• y = nummer,
• x = loggvärde.

beräkna Antilog:

y = 10x

var,

• x = nummer,
• y = antilog värde.

logaritmer och anti-logaritmer: hur det fungerar och dess betydelse

– Guide författad av Corin B. Arenas, publicerad den 1 oktober 2019

om du någonsin har undrat hur experter bestämmer stora avstånd, jordbävningsintensitet och globala ekonomiska tillväxttakter, så har du kommit till rätt ställe.

beräkning av mycket stora summor kan vara långsam och förvirrande., Men med hjälp av logaritmer (log) och antilogaritmer (antilog) kan beräkningar göras enklare.

läs vidare för att lära dig mer om log och antilog, hur de fungerar och varför dessa är relevanta matematiska begrepp.

Vad är logaritm?

en logaritm är den kraft som ett tal (kallad basen) måste multipliceras till sig själv för att få ett visst nummer. I enklare termer löser logaritm problemet:

hur många gånger multiplicerar vi b för att få ett annat nummer y?,

logaritmen räknar antalet gånger samma faktor måste multipliceras för att komma fram till ett visst nummer.

Vem kom upp med det?

Log uppfanns på 1500-talet som ett beräkningsverktyg av skotsk matematiker, fysiker och astronom, John Napier. Han skrev boken Mirifici Logarithmorum Canonis Descriptio med tabeller och siffror diskuterar naturliga logaritmer, om fastställande av grunden för dess grundläggande begrepp.

Napier myntade termen logaritm från det grekiska ordet logotyper som betyder ”förhållande eller andel” och aritmos som betyder ” nummer.,”När det kombineras betyder det bokstavligen” förhållande nummer.’

2 typer av logaritmer

den naturliga logaritmen för ett tal är dess logg till basen av konstanten e, där e är ungefär lika med 2.718281828459. Ekvationen är skriven som loge (x).

om en logaritm inte anger en bas, som det här exemplet: log(1000), är det känt som en vanlig logaritm som använder basen 10.

log(1000), Det är känt som en vanlig logaritm som använder basen 10.

Hur används loggen?,

När du börjar beräkna siffror med miljoner, miljarder och biljoner, kan det bli ganska beskatta. Oavsett om det gäller att räkna mycket pengar, befolkningens tillväxt eller täcka stora avstånd, kan log fungera för dig. Det kan förenkla stora summor som innebär långa och förvirrande ekvationer, vilket gör dem lättare att förstå.

här är standardekvationen för log:
logb (x) = y

var,

• numret multiplicerat med sig själv (B) är basen.
• antalet gånger det multipliceras (y) är logaritmen.,
• det erhållna numret (x) är skrivet i parentesen.

för att förstå hur konceptet fungerar, här är ett exempel med ett mindre antal:
fråga: hur många 2s multiplicerar vi för att få 32?
b = 2, x = 32

log2(32) = y
svar: 2 x 2 x 2 x 2 x 2 = 32

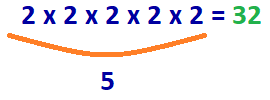
5 nummer 2s måste multipliceras för att erhålla numret 32.
svaret: log2 (32)=5

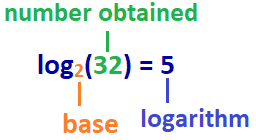
i det här exemplet: logaritmen på 32 med BAS 2 är 5, eller loggbas 2 av 32 är 5.,

dessutom är log den inversa funktionen av exponentiering, där den matematiska operationen skrivs som bn. b är basen som multipliceras enligt kraften hos n, vilket är antalet gånger det multipliceras med sig själv.

vad betyder detta? Loggen för ett tal är exponenten till vilken bas b multipliceras för att erhålla ett visst nummer. För att ge dig en bättre idé, se provloggsekvationen bredvid dess exponentiella ekvation nedan.,

logga	exponent
log2(32) = 5	25 = 32

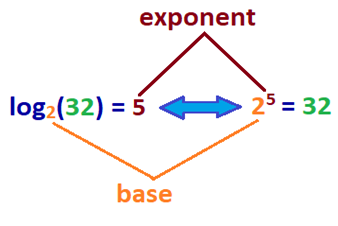
låt oss nu prova det med ett stort antal.
fråga: hur många 10s multiplicerar vi för att få 150,000,000,000?
b = 10, x = 150,000,000,000

logb(x) = y
log(150,000,000,000) = y
y = 11.1760912590557
log(150,000,000,000) = 11.,1760912590557

detta löses genom att använda loggfunktionen i en vetenskaplig kalkylator. Eller använd räknaren på den här sidan för att få svaret.

hur är Antilogaritm relaterad till loggen?

ett loggnummer kan sedan returneras till sitt ursprungliga nummer. Detta kan göras med antilogaritm (antilog). Således är antilogen den inversa funktionen av logg. På samma sätt fungerar antilog för att exponentiera ett förenklat loggvärde.,

för att beräkna antilogen för ett tal y måste du höja logaritmbasen b (vanligtvis 10, ibland konstant e) till den kraft som genererar numret y.

här är ekvationen för antilog med bas 10:
10x = y
där x är exponenten och y är antilogvärdet.

till exempel, om vi tar denna ekvation, log(5) = x, kommer dess antilog att vara 10x = 5.

• Log: log(5) = 0.698970004336019
• Antilog: 100.698970004336019 = 5

låt oss nu prova det med ett större antal.,

Om vi tar log(150,000,000,000) = x, sin antilog kommer att vara 10x = 150,000,000,000.

• Log: log10(150,000,000,000) = 11.1760912590557
• Antilog: 1011.1760912590557= 150,000,000,000

betydelse och verkliga tillämpningar

innan uppfinningen av räknare, logaritmer var används för att förenkla beräkningar inom olika kunskapsområden, såsom navigering, kartläggning, astronomi, och senare, teknik.

Föreställ dig segling i mitten av ingenstans på 1500-talet., Navigatörer förlitade sig sedan på stjärnornas position och en sextantmekanism för att fastställa deras exakta plats. Utan modern teknik för att hjälpa dig att beräkna stora avstånd kan du använda log för att förenkla dina beräkningar. Noggrannhet är viktigt, eller du riskerar fler dagar till sjöss med magra leveranser. Färre ekvationer innebär mindre utrymme för fel.

vad sägs om andra praktiska tillämpningar? Levande vetenskap stater logaritmer relaterar geometriska progressioner till aritmetiska progressioner., Om du någonsin har märkt repetitiva former och mönster i natur, arkitektur och konst, har dessa formationer sina egna motsvarande logaritmiska värden.

idag påverkar kunskap från hur dessa mönster fungerar hur mänskligheten konstruerar och designar hus, byggnader och urbana landskap.

logaritmer används också för att uttrycka omfattningen och intensiteten hos vissa skalor., Bortsett från breda avstånd och höga hastigheter mäter den andra saker som:

• ljudintensitet
• ljudfrekvens
• kraft av vindstormar
• styrka av jordbävningar
• frätande nivå av syror
• hårdhet av mineraler
• ljusstyrka av stjärnor

låt oss ta decibel som ett exempel. För att göra högtalarna starkare med 10 decibel måste den levereras med 10 gånger strömmen. När du ökar den till + 20 dB behöver den 100 gånger kraften, och med + 30 dB behöver den 1000 kraften.

dessutom fortskrider ljudintensiteten aritmetiskt., Det ändras också proportionellt med logaritmen av en ljudvåg som fortskrider geometriskt.

nedan finns en tabell från Live Science som listar olika logaritmiska skalor med motsvarande linjära skalor.

I Mäthastigheter och rankningar

enligt Kalid Azad, matematikpedagogen bakom BetterExplained.com, logaritmer är hur vi räkna ut hur snabbt något växer.

vanliga logaritmer beskriver i princip siffror när det gäller deras befogenheter på 10. När det gäller ränta är logaritmen tillväxten i en investering.,

vid fastställandet av BNP-tillväxten i ett land granskar analytikerna BNP under de följande åren. De tar BNP föregående år, och BNP följande år, sedan beräkna logaritmen för att hitta den beräknade tillväxttakten.

sökmotorer använder länkdiagrammet för att göra mål om vikten, trovärdigheten& myndighet för dokument över hela webben. Googles PageRank var en stor utveckling i sökning som ökade sök relevans och hjälpte Google search marketshare.,

enligt Azad, i en skala från 1 till 10, är en målsida med en PageRank på 2 10 gånger mer populär än en sida med en PageRank på 1. Om en webbplats har en PageRank på 5, och en konkurrentplats har en PageRank på 9, har den en skillnad på 4 storleksordningar.

en storleksordning betyder ungefär en 10x skillnad, eller en ranking är 1 siffra större jämfört med den andra. I det här fallet är en webbplats med en PageRank 9 100,000,000 mer populär än en webbplats med PageRank 1.,

den nedersta raden

Log och antilog är betydande beräkningsmetoder som gör det möjligt för oss att förenkla stora summor. Förenkling förkortar beräkningsprocessen och gör beräkningarna enklare att förstå. Detta bidrar till att minska utrymme för fel.

dessutom ger användning av log mätbara skalor för mätning av naturfenomen, som jordbävningsintensitet, vindstormarnas kraft och stjärnornas ljusstyrka. När det gäller finansiering tillåter logaritmer oss att fastställa räntor och ekonomisk tillväxt.

det används praktiskt taget inom många områden., Stora värden som beror på mätningens noggrannhet drar nytta av att använda logaritmiska beräkningar.

om författaren

Corin är en ivrig forskare och författare av finansiella ämnen—studerar ekonomiska trender, hur de påverkar befolkningen, samt hur man hjälper konsumenterna att fatta klokare finansiella beslut. Hennes övriga artiklar kan läsas på Inquirer.net och Manileno.com. Hon har en masterexamen i Kreativt Skrivande vid Universitetet i Filippinerna, en av de främsta akademiska institutioner i världen, och en Kandidatexamen i Kommunikation Konst från Miriam College.