1913 Bohr-modellen för väteatomen ersattes av Schrodingers wave mechanical model 1926. Dock är bohrsmodellen fortfarande lönsamt undervisad idag på grund av dess konceptuella och matematiska enkelhet, och eftersom den introducerade ett antal viktiga kvantmekaniska idéer som kvantantal, kvantifiering av observerbara egenskaper, kvanthopp och stationärt tillstånd.,
Bohr beräknade grenröret av tillåtna elektronenergier genom att balansera de mekaniska krafterna (centripetal och elektronkärna) på en elektron som utför en cirkulär bana av radie r om kärnan och sedan skiljemässigt kvantifiera dess vinkelmoment. Slutligen av fiat förklarade han att elektronen var i ett icke-utstrålande stationärt tillstånd eftersom en orbiting (accelererande) laddning utstrålar energi och kommer att kollapsa i den motsatta laddkärnan.,
i 1924 de Broglie postulerad våg-partikel dualitet för elektronen och andra massiva partiklar, vilket ger möjlighet att ta bort en del av skiljedomen från Bohrsmodellen. Till exempel är en elektron som har vågegenskaper föremål för konstruktiv och destruktiv störning. Som kommer att visas leder detta naturligt till kvantifiering av elektronmoment och kinetisk energi, och följaktligen en grenrör av tillåtna energitillstånd för elektronen i förhållande till kärnan., De Broglie‐Bohr-modellen av väteatomen som presenteras här behandlar elektronen som en partikel på en ring med vågliknande egenskaper.
\
de Broglies hypotes att Materia har vågliknande egenskaper.
\
konsekvensen av de Broglies hypotes; ett integrerat antal våglängder måste passa in i omkretsen av banan. Detta introducerar kvantnumret som kan ha värden 1,2,3,… N = 4-elektrontillståndet visas nedan.,
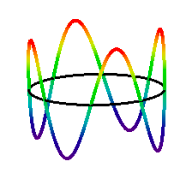
\
Substitution av den första ekvationen i den andra ekvationen visar att momentum kvantifieras.
\
om momentum kvantifieras, så är kinetisk energi.
\
vilket innebär att total energi kvantifieras. Den andra termen är elektron-proton elektrostatisk potentiell energi.
den kvantmekaniska tolkningen av dessa banor är att de är stationära tillstånd. Trots att vi använder uttrycket kinetisk energi, vilket innebär elektronrörelse, finns det ingen rörelse., Elektronen upptar banan som en partikelvåg, den kretsar inte kring kärnan. Om det kretsade i klassisk mening skulle det utstråla energi och snabbt kollapsa in i kärnan. Uppenbarligen kräver materiens stabilitet den kvantmekaniska versionen av kinetisk energi.
markstatens energi-och omloppsradie för elektronen i väteatomen finns genom att plotta energin som en funktion av orbitalradien. Marktillståndet är det minsta i den totala energikurvan., Naturligtvis kalkyl kan användas för att få samma information genom att minimera energin med avseende på omloppsbana radien. Den grafiska metoden har emellertid fördelen att belysa frågan om atomstabilitet.
grundläggande konstanter: elektronladdning, elektronmassa, Plancks konstant, vakuum permitivitet.
kvantnummer och omvandlingsfaktor mellan mätare och pikometrar och Joule och attojoule.
\
\
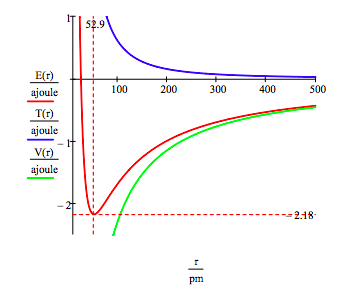
denna siffra visar att atomstabilitet innebär en balans mellan potential och kinetisk energi., Elektronen dras mot kärnan genom den attraktiva potentiella energiinteraktionen (~-1 / r), men hindras från att kollapsa in i kärnan med den extremt stora kinetiska energin (~1/R2) som är associerad med små banor.
som visas nedan kan det grafiska tillvägagångssättet också användas för att hitta de elektroniska exciterade staterna.
\
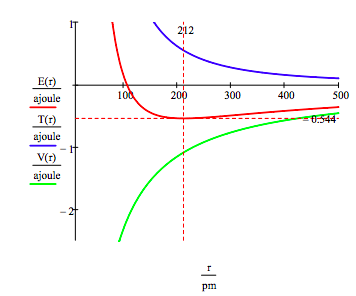
som tidigare nämnts kan grenröret av tillåtna elektronenergier också erhållas genom att minimera energin med avseende på omloppsradien. Detta förfarande ger,