Trägheitsmoment, Allgemeine Form
Da das Trägheitsmoment eines gewöhnlichen Objekts eine kontinuierliche Massenverteilung in einem ständig unterschiedlichen Abstand von jeder Rotationsachse beinhaltet, beinhaltet die Berechnung von Trägheitsmomenten im Allgemeinen Kalkül, die Disziplin der Mathematik, die solche kontinuierlichen Variablen verarbeiten kann., Da das Trägheitsmoment einer Punktmasse durch
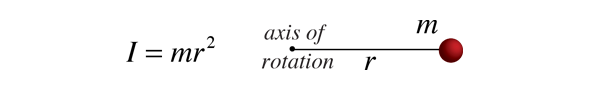
definiert ist, hat das Trägheitsmoment eines infinitesmalen Massenelements dm die gleiche Form. Diese Art von Massenelement wird als differentielles Massenelement bezeichnet und sein Trägheitsmoment ist gegeben durch
Beachten Sie, dass das differentielle Element des Trägheitsmoments dI immer in Bezug auf eine bestimmte Rotationsachse definiert werden muss., Die Summe über all diesen Massenelementen wird als Integral über der Masse bezeichnet.
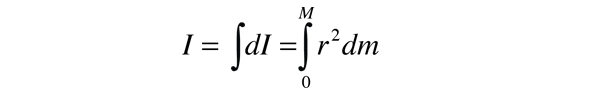
Normalerweise wird das Massenelement dm in der Geometrie des Objekts ausgedrückt, so dass die Integration über das Objekt als Ganzes (z. B. über einen langen einheitlichen Stab) durchgeführt werden kann.
Nachdem dies als allgemeine Form bezeichnet wurde, ist es wahrscheinlich angebracht darauf hinzuweisen, dass es sich nur um eine allgemeine Form für Achsen handelt, die als „Hauptachsen“ bezeichnet werden können, ein Begriff, der alle Symmetrieachsen von Objekten umfasst., Das Konzept des Trägheitsmoments für allgemeine Objekte über beliebige Achsen ist ein viel komplizierteres Thema. Das Trägheitsmoment hat in solchen Fällen die Form einer mathematischen Tensorgröße, für deren vollständige Definition neun Komponenten erforderlich sind.
| Beispiele für die integration erhalten Trägheitsmoment. | Gerader Stab |
| Zylinder | |
| Kugel |