
O scurtă explicație și o dovadă
Rațională Rădăcină Teorema (RRT) este un instrument la îndemână pentru a avea în matematică arsenal. Acesta oferă și test rapid și murdar pentru raționalitatea unor expresii. Și ajută la găsirea rădăcinilor raționale ale polinoamelor.,
Iată cum și de ce funcționează.,e53714″>
Cum
să Presupunem că aveți un polinom de gradul n cu coeficienti:

Rațională Rădăcină Teorema afirmă: Dacă o rădăcină rațională există, apoi componentele sale se vor împărți primul și ultimul coeficienți:

rațională rădăcină este exprimat în mai mică termeni., Asta înseamnă că P și q nu au factori comuni. (Asta va fi important mai târziu.) Numărătorul împarte Constanta la sfârșitul polinomului; demominatorul împarte coeficientul principal.
Ca un exemplu:
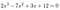
Avem nevoie de uita doar la 2 și 12.,:
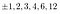
The factors of 2:
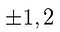
Thus, if a rational root does exist, it’s one of these:
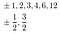
Plug each of these into the polynomial., Which one(s) — if any solve the equation? If none do, there are no rational roots.
Are any cube roots of 2 rational? A rational root, p/q must satisfy this equation.
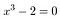
Furthermore:
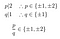
Not one of these candidates qualifies., Salt la:
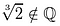
Ce
Să mergem înapoi la paradigma noastră polinom.,

Scoot the constant to the other side:

Now, plug in our rational root, p/q.,

Multiplica totul de qⁿ:

Fiecare termen pe partea stângă a p în comun. Factor care afară.,

Arată mult mai rău decât trebuie să fie. Să înlocuim toate chestiile astea în paranteză cu un S. Nu ne pasă cu adevărat ce este acolo.
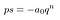
este mult mai ușor de pe ochi.nu uitați că p și q sunt numere întregi. De asemenea, nu au factori comuni., Prin urmare, p nu poate împărți qⁿ. Acesta trebuie să împartă a₀:
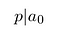
Astfel, numărătorul se divide termenul constant.
Acum, du-te înapoi la paradigma noastră polinom:

de Această dată, rău la primul termen la dreapta.,

Insert the rational root:

As before, multiply by qⁿ.

This time, the common factor on the left is q., Let’s extract it, and lump together the remaining sum as t.
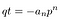
Again, q and p have no common factors. Therefore:
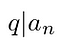
Thus proves the rational root theorem.