Teorema lui Bayes găsește multe utilizări în teoria probabilităților și statistici. Există o mică șansă să nu fi auzit niciodată despre această teoremă în viața ta. Se pare că această teoremă și-a găsit drumul în lumea învățării automate, pentru a forma unul dintre algoritmii foarte decorați. În acest articol, vom afla totul despre algoritmul naiv Bayes, împreună cu variațiile sale pentru diferite scopuri în învățarea mașinilor.după cum probabil ați ghicit, acest lucru ne cere să privim lucrurile dintr-un punct de vedere probabilistic., La fel ca în învățarea automată, avem atribute, variabile de răspuns și predicții sau clasificări. Folosind acest algoritm, vom avea de-a face cu distribuțiile de probabilitate ale variabilelor din setul de date și vom prezice probabilitatea variabilei de răspuns aparținând unei anumite valori, având în vedere atributele unei noi instanțe. Să începem prin revizuirea teoremei lui Bayes.
Teorema lui Bayes
Acest lucru ne permite să examinăm probabilitatea unui eveniment bazat pe cunoașterea anterioară a oricărui eveniment legat de evenimentul anterior., Deci, de exemplu, probabilitatea ca prețul unei case este mare, poate fi mai bine evaluată dacă cunoaștem facilitățile din jurul ei, în comparație cu evaluarea făcută fără cunoașterea locației casei. Teorema lui Bayes face exact asta.

De mai sus ecuația dă reprezentare de bază teorema lui Bayes., Aici A și B sunt două evenimente și,
P (A / B): probabilitatea condiționată ca evenimentul A să apară , având în vedere că B a avut loc. Aceasta este, de asemenea, cunoscută sub numele de probabilitatea posterioară.
P (A) și P(B): probabilitatea de A și B, fără a ține seama unul de altul.
P (B / A) : probabilitatea condiționată ca evenimentul B să apară , având în vedere că A a avut loc.acum, să vedem cum acest lucru se potrivește bine scopului învățării automate.,luați o problemă simplă de învățare automată, în care trebuie să învățăm modelul nostru dintr-un set dat de atribute(în exemplele de instruire) și apoi să formăm o ipoteză sau o relație cu o variabilă de răspuns. Apoi folosim această relație pentru a prezice un răspuns, având în vedere atributele unei noi instanțe. Folosind teorema lui Bayes, este posibil să se construiască un elev care prezice probabilitatea variabilei de răspuns aparținând unei clase, având în vedere un nou set de atribute.
luați în considerare ecuația anterioară din nou. Acum, să presupunem că A este variabila de răspuns și B este atributul de intrare., Deci, conform ecuației, avem
P(A / B) : probabilitatea condiționată a variabilei de răspuns aparținând unei anumite valori, având în vedere atributele de intrare. Aceasta este, de asemenea, cunoscută sub numele de probabilitatea posterioară.
P (A): Probabilitatea anterioară a variabilei de răspuns.
P (B): probabilitatea de formare a datelor sau a dovezilor.
P (B / A) : Acest lucru este cunoscut ca probabilitatea datelor de formare.,
prin Urmare, ecuația de mai sus poate fi rescris a ca
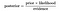
Să aruncăm o problemă, în cazul în care numărul de atribute este egal cu n, iar răspunsul este o valoare boolean, adică poate fi în una din cele două clase. De asemenea, atributele sunt categorice(2 categorii pentru cazul nostru). Acum, pentru a instrui clasificatorul, va trebui să calculăm P (B / A), pentru toate valorile din instanță și spațiul de răspuns., Aceasta înseamnă că va trebui să calculăm 2 * (2^n -1), parametrii pentru învățarea acestui model. Acest lucru este în mod clar nerealist în majoritatea domeniilor de învățare practice. De exemplu, dacă există 30 de atribute booleene, atunci va trebui să estimăm mai mult de 3 miliarde de parametri.
algoritmul Bayes naiv
complexitatea Clasificatorului Bayesian de mai sus trebuie redusă, pentru ca acesta să fie practic. Algoritmul naiv Bayes face acest lucru prin asumarea Independenței condiționate față de setul de date de formare. Acest lucru reduce drastic complexitatea problemei menționate mai sus la doar 2n.,
ipoteza de independență condiționată afirmă că, având în vedere variabile aleatoare X, Y și Z, spunem ca X este condiționat independente de Y dat Z, dacă și numai dacă distribuția de probabilitate care reglementează X este independentă de valoarea lui Y dat Z.
cu alte cuvinte, X și Y sunt condiționat independente dat Z dacă și numai dacă, având în vedere cunoștințele pe care Z are loc, cunoștințe dacă X apare nu oferă informații cu privire la probabilitatea de Y care apar, și cunoștințe dacă Y apare nu oferă informații cu privire la probabilitatea de X care apar.,
această ipoteză face algoritmul Bayes, naiv.
Dat, n diferite valori ale atributelor, probabilitatea acum poate fi scris ca
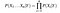
Aici, X reprezintă atribute sau caracteristici, și Y este variabilă de răspuns. Acum, P (X|Y) devine egal cu produsele, distribuția probabilității fiecărui atribut x dat Y.,
maximizarea a Posteriori
ceea ce ne interesează este găsirea probabilității posterioare sau P(Y|X). Acum, pentru mai multe valori ale lui Y, va trebui să calculăm această expresie pentru fiecare dintre ele.având în vedere o nouă instanță Xnew, trebuie să calculăm probabilitatea ca Y să preia orice valoare dată, având în vedere valorile atributelor observate ale Xnew și având în vedere distribuțiile P(Y) și P(X|Y) estimate din datele de antrenament.deci ,cum vom prezice clasa variabilei de răspuns, pe baza diferitelor valori pe care le atingem pentru P(Y|X)., Pur și simplu luăm cea mai probabilă sau maximă dintre aceste valori. Prin urmare, această procedură este cunoscută și sub denumirea de maximizare a posteriori.dacă presupunem că variabila de răspuns este distribuită uniform, adică este la fel de probabil să primească orice răspuns, atunci putem simplifica și mai mult algoritmul. Cu această ipoteză, priori sau P (Y) devine o valoare constantă, care este 1/categorii ale răspunsului.deoarece priori și dovezile sunt acum independente de variabila de răspuns, acestea pot fi eliminate din ecuație., Prin urmare, maximizarea posteriori se reduce la maximizarea problemei probabilității.după cum se vede mai sus, trebuie să estimăm distribuția variabilei de răspuns din setul de antrenament sau să presupunem o distribuție uniformă. În mod similar, pentru a estima parametrii pentru distribuția unei caracteristici, trebuie să presupunem o distribuție sau să generăm modele neparametrice pentru caracteristicile din setul de instruire. Astfel de ipoteze sunt cunoscute sub numele de modele de evenimente. Variațiile acestor ipoteze generează algoritmi diferiți pentru scopuri diferite., Pentru distribuții continue, Gaussian naive Bayes este algoritmul de alegere. Pentru caracteristici discrete, distribuțiile multinomiale și Bernoulli sunt la fel de populare. Discutarea detaliată a acestor variații nu intră în domeniul de aplicare al acestui articol.clasificatorii naivi Bayes funcționează foarte bine în situații complexe, în ciuda ipotezelor simplificate și a naivității. Avantajul acestor clasificatori este că acestea necesită un număr mic de date de formare pentru estimarea parametrilor necesari pentru clasificare. Acesta este algoritmul de alegere pentru clasificarea textului., Aceasta este ideea de bază din spatele Clasificatorilor naivi Bayes, că trebuie să începeți să experimentați algoritmul.