forme tridimensionale: poliedre, solide curbate și suprafață

Această pagină examinează proprietățile formelor tridimensionale sau „solide”.o formă bidimensională are lungime și lățime. O formă solidă tridimensională are și adâncime. Formele tridimensionale, prin natura lor, au un interior și un exterior, separate de o suprafață. Toate elementele fizice, lucrurile pe care le puteți atinge, sunt tridimensionale.,această pagină acoperă atât solidele drepte numite poliedre, care se bazează pe poligoane, cât și solidele cu curbe, cum ar fi Globurile, Cilindrii și conurile.

Poliedrele

Poliedrele (sau poliedrele) sunt forme solide drepte. Poliedrele se bazează pe poligoane, forme plane bidimensionale cu linii drepte.

consultați proprietățile paginii noastre de poligoane pentru mai multe informații despre lucrul cu poligoane.

Poliedrele sunt definite ca având:

• margini drepte.
• fețe plate numite fețe.,
• colțuri, numite noduri.Poliedrele sunt, de asemenea, adesea definite de numărul de margini, fețe și vârfuri pe care le au, precum și dacă fețele lor au aceeași formă și dimensiune. La fel ca poligoanele, poliedrele pot fi regulate (bazate pe poligoane regulate) sau neregulate (bazate pe poligoane neregulate). Poliedrele pot fi, de asemenea, concave sau convexe. unul dintre poliedrele cele mai de bază și familiare este cubul. Un cub este un poliedru obișnuit, având șase fețe pătrate, 12 margini și opt vârfuri.,
  

  Poliedre Regulate (Solide Platonice)

  Cele cinci corpuri regulate sunt o clasă specială de poliedre, ale cărui fețe sunt identice cu fiecare față fiind un poligon regulat. Solidele platonice sunt:

  • tetraedru cu patru fețe triunghiulare echilaterale.
  • cub cu șase fețe pătrate.
  • octaedru cu opt fețe triunghi echilateral.
  • dodecaedru cu douăsprezece fețe pentagon.
  • icosaedru cu douăzeci de fețe triunghi echilateral.,

  vezi diagrama de mai sus pentru o ilustrare a fiecăruia dintre aceste poliedre obișnuite.

  ce este o prismă?

  o prismă este orice poliedru care are două capete de potrivire și laturi plate. Dacă tăiați o prismă oriunde de-a lungul lungimii sale, paralel cu un capăt, secțiunea sa transversală este aceeași – ați ajunge la două prisme. Laturile unei prisme sunt paralelograme-forme pe patru fețe cu două perechi de laturi cu lungime egală.

  Antiprismele sunt similare cu prismele obișnuite, capetele lor se potrivesc., Cu toate acestea, laturile anti-prismelor sunt alcătuite din triunghiuri și nu paralelograme. Antiprismele pot deveni foarte complexe.

  ce este o piramidă?

  o piramidă este un poliedru cu o bază poligonală care se conectează la un vârf (punctul de sus) cu laturi drepte.deși avem tendința să ne gândim la piramide cu o bază pătrată, precum cele pe care le-au construit vechii egipteni, ele pot avea de fapt orice bază poligonală, regulată sau neregulată. În plus, o piramidă poate avea un vârf în centrul direct al bazei sale, o piramidă dreaptă sau poate avea vârful în afara centrului atunci când este o piramidă oblică.,

  

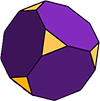
  poliedre mai complexe

  există multe alte tipuri de poliedre: simetrice și asimetrice, concave și convexe. solidele Arhimedene, de exemplu, sunt alcătuite din cel puțin două poligoane regulate diferite. cubul trunchiat (așa cum este ilustrat) este un solid Arhimedean cu 14 fețe. 6 dintre fețe sunt octagoane regulate, iar celelalte 8 sunt triunghiuri regulate (echilaterale). Forma are 36 de muchii și 24 de vârfuri (colțuri).,formele tridimensionale cu curbe formele solide care includ o margine curbată sau rotundă nu sunt poliedre. Poliedrele pot avea doar laturi drepte.multe dintre obiectele din jurul tău vor include cel puțin câteva curbe. În geometrie, cele mai comune solide curbate sunt cilindrii, conurile, sferele și tori (pluralul pentru torus).,

  Comune Forme Tridimensionale cu Curbe:
  Cilindru	Con
  Un cilindru are aceeași secțiune transversală de la un capăt la altul. Cilindrii au două capete identice fie ale unui cerc, fie ale unui oval. Deși similare, Cilindrii nu sunt prisme ca o prismă are (prin definiție) paralelogram, laturi plate.,	un con are o bază circulară sau ovală și un vârf (sau vârf). Partea conului se înclină ușor spre vârf. Un con este similar cu o piramidă, dar distinct ca un con are o singură latură curbată și o bază circulară.
  Sferă	Tor
  în Formă de o minge sau un glob o sferă este un obiect rotund. Fiecare punct de pe suprafața unei sfere este o distanță egală cu centrul sferei.,	în formă de inel, anvelopă sau gogoașă, un torus inel obișnuit este format prin rotirea unui cerc mai mic în jurul unui cerc mai mare. Există, de asemenea, o formă mai complexă de tori.

  suprafața

  pagina noastră de calcul a suprafeței explică modul de elaborare a zonei formelor bidimensionale și trebuie să înțelegeți aceste elemente de bază pentru a calcula suprafața formelor tridimensionale.pentru formele tridimensionale, vorbim despre suprafață, pentru a evita confuzia.,puteți utiliza cunoștințele dvs. despre aria formelor bidimensionale pentru a calcula suprafața unei forme tridimensionale, deoarece fiecare față sau parte este efectiv o formă bidimensională.prin urmare, elaborați zona fiecărei fețe și apoi adăugați-le împreună.ca și în cazul formelor plate, suprafața unui solid este exprimată în unități pătrate: cm2, inches2, m2 și așa mai departe. Puteți găsi mai multe detalii despre unitățile de măsură pe pagina noastră sisteme de măsurare.,

  Exemple de calcule ale suprafeței

  

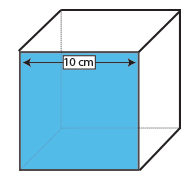
  cub

  suprafața unui cub este aria unei fețe (lungime x Lățime) înmulțită cu 6, deoarece toate cele șase fețe sunt aceleași.deoarece fața unui cub este un pătrat, trebuie doar să faceți o singură măsurătoare – lungimea și lățimea unui pătrat sunt, prin definiție, aceleași.prin urmare, o față a acestui cub este de 10 × 10 cm = 100cm2. Înmulțiți cu 6, Numărul de fețe pe un cub și descoperim că suprafața acestui cub este de 600cm2.,în mod similar, suprafața celorlalte poliedre obișnuite (solide platonice) poate fi elaborată prin găsirea zonei unei părți și apoi înmulțirea răspunsului cu numărul total de laturi – vezi diagrama poliedrelor de bază de mai sus.dacă suprafața unui pentagon care formează un dodecaedru este de 22cm2, atunci înmulțiți acest lucru cu numărul total de laturi (12) pentru a da răspunsul 264cm2.,

  Piramida

  pentru a calcula suprafața unei piramide standard cu patru laturi triunghiulare egale și o bază pătrată:

  Mai întâi elaborați aria bazei (pătrat) lungime × lățime.

  următorul lucru din zona de o parte (triunghi). Măsurați lățimea de-a lungul bazei și apoi înălțimea triunghiului (cunoscută și sub denumirea de lungime înclinată) de la punctul central de pe bază până la vârf.,puteți fie să împărțiți răspunsul cu 2 pentru a vă oferi suprafața unui triunghi și apoi să înmulțiți cu 4 pentru a da suprafața tuturor celor patru laturi, fie pur și simplu să multiplicați suprafața unui triunghi cu 2.în cele din urmă adăugați zona bazei și laturile împreună pentru a găsi suprafața totală a piramidei.pentru a calcula suprafața altor tipuri de piramide, adăugați împreună zona bazei (cunoscută sub numele de zona de bază) și zona laturilor (zona laterală), poate fi necesar să măsurați laturile individual.,o plasă geometrică este un „model” bidimensional pentru un obiect tridimensional. Plasele pot fi de ajutor atunci când se lucrează la suprafața unui obiect tridimensional. În diagrama de mai jos puteți vedea cum sunt construite piramidele de bază, dacă piramida este „desfăcută”, rămâneți cu plasa.

  

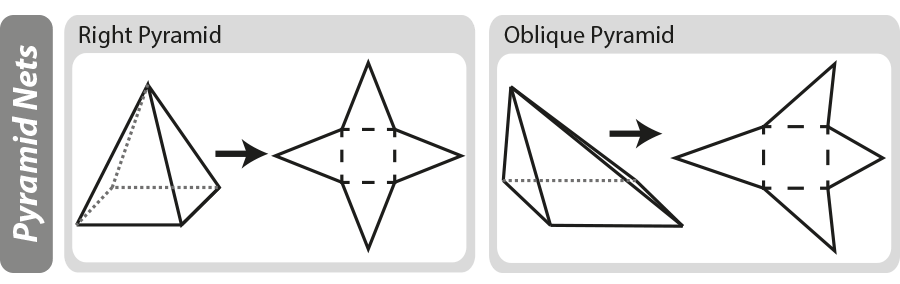
  Pentru mai multe informații despre diagramele nete, consultați pagina noastră forme și plase 3d.

  

  prismă

  pentru a calcula suprafața unei prisme:

  Prismele au două capete aceleași și laturile paralelogram plate.,calculați aria unui capăt și înmulțiți cu 2.pentru o prismă obișnuită (unde toate laturile sunt aceleași) calculați aria uneia dintre laturi și înmulțiți cu numărul total de laturi.pentru prisme neregulate (cu laturi diferite) calculați aria fiecărei părți.adăugați cele două răspunsuri împreună (capete × laturi) pentru a găsi suprafața totală a prismei.,

  Cilindru

  

  Exemplu:
  Raza = 5cm
  Inaltime = 10cm

  Pentru a calcula suprafața unui cilindru este util să se gândească la componente de forma. Imaginați-vă un cositor de porumb dulce – are un vârf și un fund, ambele fiind cercuri. Dacă tăiați partea de-a lungul lungimii sale și o aplatizați, veți avea un dreptunghi. Prin urmare, trebuie să găsiți zona a două cercuri și un dreptunghi.mai întâi elaborați zona unuia dintre cercuri.

  aria unui cerc este π (pi) × radius2.,presupunând o rază de 5cm, aria unuia dintre cercuri este de 3,14 × 52 = 78, 5cm2.înmulțiți răspunsul cu 2, deoarece există două cercuri 157cm2

  zona laterală a cilindrului este perimetrul cercului × înălțimea cilindrului.

  perimetrul este egal cu π x 2 × raza. În exemplul nostru, 3.14 × 2 × 5 = 31.4

  măsurați înălțimea cilindrului-pentru acest exemplu înălțimea este de 10 cm. Suprafața laturii este de 31,4 × 10 = 314cm2.,

  suprafața totală poate fi găsit prin adăugarea în zona de cercuri și o parte împreună:

  157 + 314 = 471cm2

  

  Exemplu:
  Raza = 5cm
  Lungimea Înclinată = 10cm

  Con

  atunci Când se calculează suprafața unui con aveți nevoie pentru a utiliza lungimea ‘înclinat’ precum și raza de la baza.cu toate acestea, este relativ simplu de calculat:

  aria cercului de la baza conului este π(pi) × radius2.

  în acest exemplu suma este 3.14 × 52 = 3.14 × 25 = 78.,5cm2

  aria laturii, secțiunea înclinată, poate fi găsită folosind următoarea formulă:

  π(pi) × raza × lungimea înclinată.

  în exemplul nostru suma este 3.14 × 5 × 10 = 157cm2.în cele din urmă adăugați zona de bază în zona laterală pentru a obține suprafața totală a conului.

  78.5 + 157 = 235.5cm2

  

  Minge de Tenis:
  Diametru = 2.6 inch

  Sferă

  suprafața unei sfere este un relativ simplu de expansiune de formula pentru un cerc zona.

  4 × π × radius2.,pentru o sferă este adesea mai ușor să se măsoare diametrul-distanța de-a lungul sferei. Puteți găsi apoi raza care este jumătate din diametru.diametrul unei mingi de tenis standard este de 2,6 inci. Raza este, prin urmare, de 1, 3 inci. Pentru formula avem nevoie de raza pătrat. 1.3 × 1.3 = 1.69.

  suprafața unei mingi de tenis este, prin urmare:

  4 × 3,14 × 1,69 = 21,2264 inchi2.,

  

  Exemplu:
  R (Raza Mare) = 20 cm
  r (Rază Mică) = 4 cm

  Tor

  pentru a calcula suprafața de un tor aveți nevoie pentru a găsi două rază de valori.

  raza mare sau majoră (R) este măsurată de la mijlocul găurii până la mijlocul inelului.

  raza mică sau minoră (r) este măsurată de la mijlocul inelului până la marginea exterioară.diagrama prezintă două vederi ale unui exemplu de torus și modul de măsurare a radiuselor sale (sau raze).,calculul pentru a găsi suprafața este în două părți (una pentru fiecare rază). Calculul este același pentru fiecare parte.

  formula este: Suprafață = (2NR) (2NR)

  pentru a lucra suprafața exemplului torus.

  (2 × π × R) = (2 × 3.14 × 20) = 125.6

  (2 × π × r) = (2 × 3.14 × 4) = 25.12

  înmulțiți cele două răspunsuri împreună pentru a găsi suprafața totală a exemplului torus.