O Racional Raiz Teorema

Como

Suponha que você tenha um polinˆ omio de grau n, com coeficientes inteiros:

O Racional Raiz Teorema afirma: Se uma raiz racional existe, em seguida, os seus componentes vão dividir o primeiro e o último coeficientes:

O racional raiz é expressa em termos mais baixos., Isso significa que p e q não compartilham fatores comuns. (Isso será importante mais tarde. O numerador divide a constante no final do polinômio; o desmominador divide o coeficiente líder.

Como um exemplo:

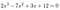
Nós só precisamos olhar para o 2 e o 12.,:

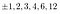
The factors of 2:

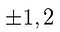
Thus, if a rational root does exist, it’s one of these:

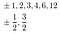
Plug each of these into the polynomial., Which one(s) — if any solve the equation? If none do, there are no rational roots.

Are any cube roots of 2 rational? A rational root, p/q must satisfy this equation.

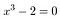
Furthermore:

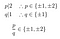
Not one of these candidates qualifies., Saltar para:

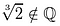
Por

Let’s go back para o nosso paradigma polinomial.,

Scoot the constant to the other side:

Now, plug in our rational root, p/q.,

Multiplique tudo por qⁿ:

Cada termo à esquerda tem p em comum. Põe isso de lado.,

Parece muito pior do que ele precisa ser. Vamos substituir tudo isso entre parênteses por um s. Não nos interessa o que está lá dentro.

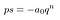
Que é muito mais fácil sobre os olhos.

lembre-se que P E q são inteiros. Também não partilham factores comuns., Portanto, p não pode dividir qⁿ. Ele deve dividir a₀:

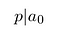
Assim, o numerador divide o termo constante.

Agora, volte para o nosso paradigma polinomial:

Neste momento, o ruim é o primeiro termo do lado direito.,

Insert the rational root:

As before, multiply by qⁿ.

This time, the common factor on the left is q., Let’s extract it, and lump together the remaining sum as t.

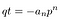
Again, q and p have no common factors. Therefore:

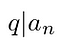
Thus proves the rational root theorem.