Localizar as Funções Quadráticas para um Dado Parábolas
Há muitos tipos diferentes de problemas que podem ser feitas com relação às equações de segundo grau. Neste artigo, o foco será colocado sobre como podemos desenvolver uma equação quadrática a partir de um grafo quadrático usando um par de métodos diferentes., Mas, antes de entrarmos nesses tipos de problemas, dedique um momento para brincar com expressões quadráticas nesta maravilhosa calculadora de gráficos online aqui. Quanto mais confortável estiver com gráficos quadráticos e expressões, mais fácil será este tópico!agora vamos resolver problemas com esse conhecimento, ou seja, como encontrar a equação de uma parábola!
como encontrar uma equação quadrática a partir de um grafo:
a fim de encontrar uma equação quadrática a partir de um grafo, existem dois métodos simples que se pode empregar: usando 2 pontos, ou usando 3 pontos.,
1) Encontrar equação quadrática a partir de 2 Pontos
A fim de encontrar uma equação quadrática a partir de um grafo usando apenas 2 Pontos, um desses pontos deve ser o vértice. Com o vértice e um outro ponto, nós podemos sub-las para o que é chamado de “forma de vértice” e então resolver para a nossa equação., O vértice a fórmula é a seguinte, onde (d,f) é o vértice e ponto (x,y) é o outro ponto:
Vértice formulário também pode ser escrito na sua forma mais “adequada” do formulário, como:
Usando esta fórmula, tudo o que precisamos fazer é sub no vértice e o outro ponto, resolver para um, e, em seguida, reescrever nossa equação final., A melhor maneira de ficar confortável com o uso deste formulário é fazer um problema de exemplo com ele.
exemplo:
determina a equação da parábola mostrada na imagem abaixo.
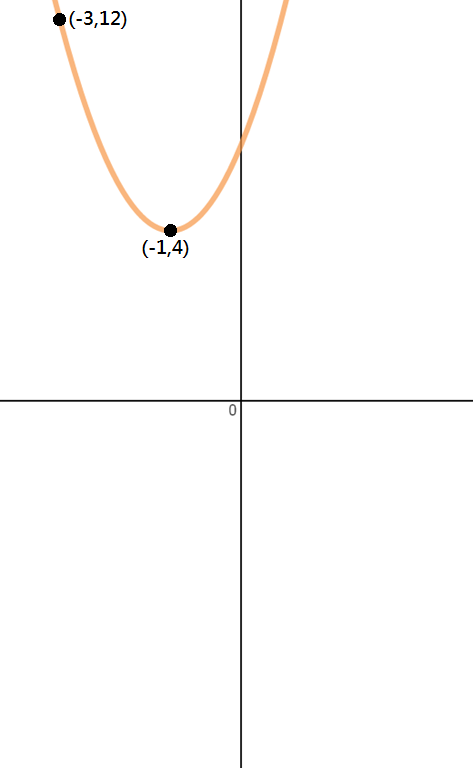
Passo 1: Identificar Pontos
uma vez que estamos apenas dois pontos neste problema, o vértice e outro ponto, devemos usar o vértice formulário para resolver esta questão.,
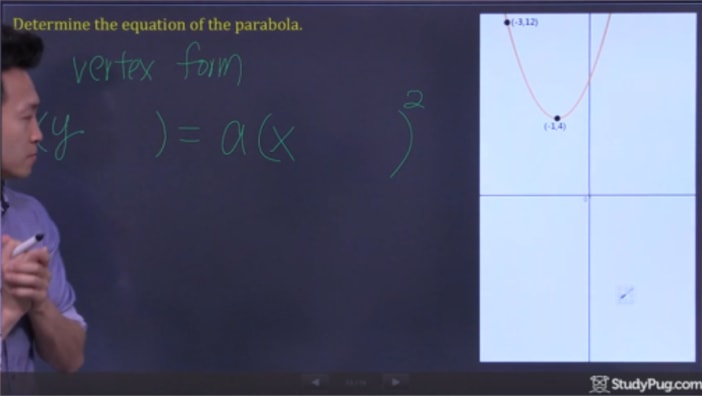
Passo 2: Sub-Pontos No Vértice Formulário e Resolver para “a”
Agora, tudo o que temos a fazer é sub em nossos dois pontos para o vértice fórmula e resolver para “a” para ter todas as informações para escrever o nosso final equação quadrática.,4)=um(-3+1)2(12 – 4) = um(-3 + 1)^{2}(12-4)=um(-3+1)2
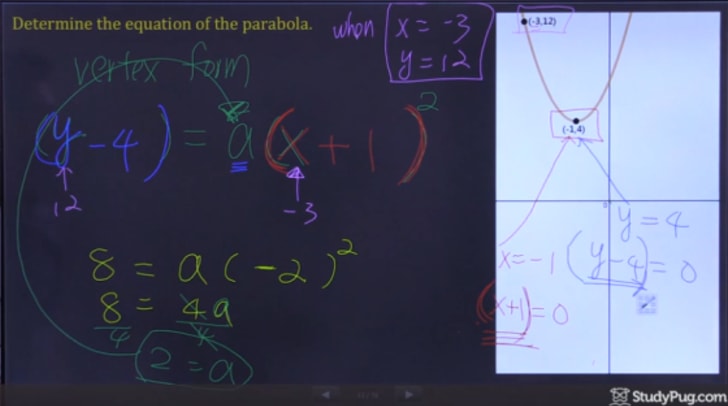
Passo 3: Escreva Equação Quadrática
Após a solução para “a”, agora temos todas as informações de que precisamos para escrever a nossa resposta final.,
E, em seguida, em boa vértice forma de uma parábola, a nossa resposta final é:
Que conclui a lição no vértice formulário e como encontrar uma equação quadrática a partir de 2 pontos!, Se você quiser atualizar sua memória sobre os tópicos relacionados, tais como, como resolver expressões quadráticas na forma de vértices, como converter uma equação quadrática regular de formulário padrão para forma de vértices, completando o quadrado, e como usar a fórmula de vértices, certifique-se de verificar nossas lições.
2) Encontrar equação quadrática a partir de 3 pontos
em alguns casos, não teremos tanta sorte a ponto no vértice. Se for esse o caso, não podemos mais encontrar a expressão quadrática usando apenas dois pontos, e precisamos fazer algo um pouco diferente., No caso em que nos são dadas informações sobre as intercepções x de uma parábola, bem como um outro ponto, podemos encontrar a equação quadrática usando uma equação que é chamada de “forma factored”. A equação geral para a forma fatorada fórmula é a seguinte, com a, b e c, sendo o x-valores das coordenadas x intercepta:
Usando esta fórmula, tudo o que precisamos fazer é sub coordenadas x-x intercepta, outro ponto e, em seguida, resolver para um assim, podemos escrever a nossa resposta final., Novamente, a melhor maneira de ficar confortável com esta forma de equações quadráticas é fazer um problema de exemplo.
Exemplo:
Determine a equação da parábola é mostrado na imagem abaixo:
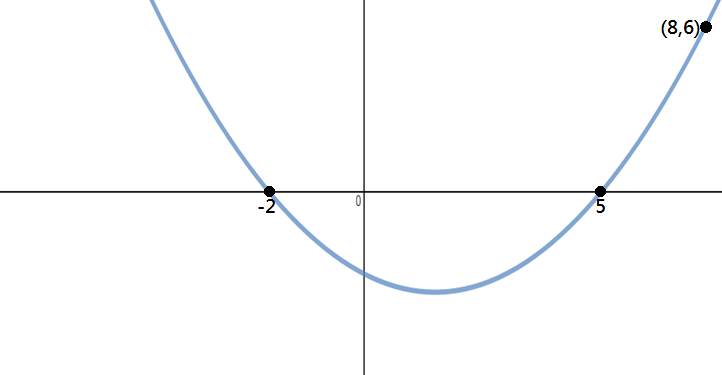
Passo 1: Identificar Pontos
Desde que nos são dados três pontos neste problema, o x-intercepta e outro ponto, podemos usar a forma fatorada para resolver esta questão.,
do gráfico, podemos ver que OS X-interceptos são -2 e 5, e o ponto na parábola é (8,6).
Passo 2: sub-pontos em forma de vértice e resolver para ” a “
Agora tudo o que temos a fazer é sub-em nossos valores na fórmula de forma factorada e resolver para” a ” ter toda a informação para escrever a nossa equação quadrática final.,(x – 5)y=(x+2)(x−5)
em seguida, podemos usar o ponto da parábola (8,6) para resolver “um”:
Passo 3: Escrever Equação Quadrática
Após a solução para “a”, agora temos todas as informações de que precisamos para escrever a nossa resposta final.,
E aquele é todo lá é-lhe! Estes são os dois métodos mais importantes para encontrar uma função quadrática a partir de uma dada parábola. Para mais estudos sobre funções quadráticas e seus gráficos, confira esses vídeos úteis lidando com as desigualdades quadráticas discriminantes, graficantes e cónicas.