Bayes’ theorem finds many uses in the probability theory and statistics. Há uma micro chance de você nunca ter ouvido falar deste teorema em sua vida. Acontece que este teorema encontrou seu caminho para o mundo da aprendizagem de máquinas, para formar um dos algoritmos altamente decorados. Neste artigo, vamos aprender tudo sobre o algoritmo ingênuo Bayes, juntamente com suas variações para diferentes propósitos na aprendizagem de máquinas.
Como você poderia ter adivinhado, isto requer que vejamos as coisas de um ponto de vista probabilístico., Assim como na aprendizagem de máquinas, temos atributos, variáveis de resposta e predições ou classificações. Usando esse algoritmo, estaremos lidando com as distribuições de probabilidade das variáveis no conjunto de dados e prevendo a probabilidade da variável de resposta pertencentes a um determinado valor, dada a atributos de uma nova instância. Vamos começar por rever o teorema de Bayes.
Teorema de Bayes
isto permite-nos examinar a probabilidade de um evento baseado no conhecimento prévio de qualquer evento relacionado com o evento anterior., Assim, por exemplo, a probabilidade de o preço de uma casa ser elevado, pode ser melhor avaliada se conhecermos as instalações à sua volta, em comparação com a avaliação feita sem o conhecimento da localização da casa. O teorema de Bayes faz exatamente isso.

Equação acima dá a representação básica de Bayes’ teorema., Aqui A E B são dois eventos e,
P (A / B): a probabilidade condicional de que o evento a ocorra , dado que B ocorreu. Isto também é conhecido como probabilidade posterior.
P(A) E P(B) : probabilidade de A E B sem consideração entre si.
P (B / A): a probabilidade condicional de que o evento B ocorra , dado que A ocorreu.agora, vamos ver como isso se adequa bem ao propósito de aprendizagem de máquinas.,
tomar um simples problema de aprendizagem de máquina, onde precisamos aprender nosso modelo a partir de um determinado conjunto de atributos(em exemplos de treinamento) e, em seguida, formar uma hipótese ou uma relação com uma variável de resposta. Então usamos esta relação para prever uma resposta, dados atributos de uma nova instância. Usando o teorema de Bayes, é possível construir um aprendiz que prevê a probabilidade da resposta variável pertencente a alguma classe, dado um novo conjunto de atributos.
considere a equação anterior novamente. Agora, suponha que A é a variável de resposta e B é o atributo de entrada., Assim, de acordo com a equação, temos
P(A|B) : probabilidade condicional de variável de resposta pertencente a um determinado valor, dado os atributos de entrada. Isto também é conhecido como probabilidade posterior.
P(A): a probabilidade prévia da variável de resposta.
P(B): a probabilidade dos dados de formação ou da evidência.
P(B / A): isto é conhecido como a probabilidade dos dados de formação.,
Portanto, a equação acima pode ser reescrita como:
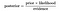
Vamos ter um problema, onde o número de atributos é igual a n e a resposta é um valor booleano, por exemplo, ele pode estar em uma das duas classes. Além disso, os atributos são categóricos(2 categorias para o nosso caso). Agora, para treinar o classificador, vamos precisar calcular P (B|A), para todos os valores no espaço de instância e resposta., Isto significa que vamos precisar calcular 2 * (2^n-1), parâmetros para aprender este modelo. Isto é claramente irrealista na maioria dos domínios práticos de aprendizagem. Por exemplo, se existem 30 atributos booleanos, então precisaremos estimar mais de 3 bilhões de parâmetros.
algoritmo ingênuo de Bayes
a complexidade do Classificador Bayesiano acima precisa ser reduzida, para que seja prático. O algoritmo ingênuo de Bayes faz isso assumindo uma independência condicional sobre o conjunto de dados de treinamento. Isso reduz drasticamente a complexidade do problema acima mencionado para apenas 2n.,
O pressuposto de independência condicional afirma que, dadas as variáveis aleatórias X, Y e Z, dizemos que X é condicionalmente independente de Y dado Z, se e somente se a distribuição de probabilidade que rege X é independente do valor de Y dado Z.
Em outras palavras, X e Y são condicionalmente independentes dado Z se, e somente se, dado o conhecimento que Z ocorre, o conhecimento se X ocorre não fornece nenhuma informação sobre a probabilidade de Y ocorrendo, e o conhecimento se Y ocorre não fornece nenhuma informação sobre a probabilidade de X ocorrer.,
esta suposição torna o algoritmo de Bayes ingênuo.
Dado, n valores de atributo diferentes, a probabilidade de agora pode ser escrito como
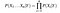
Aqui, o X representa os atributos ou características, e Y é a variável de resposta. Agora, P (X|Y) torna-se igual aos produtos de, distribuição de probabilidade de cada atributo x dado Y.,
maximizando a Posteriori
aquilo em que estamos interessados, é encontrar a probabilidade posterior ou P(Y|X). Agora, para vários valores de Y, vamos precisar calcular esta expressão para cada um deles.
Dada uma nova instância Xnew, precisamos calcular a probabilidade de que Y vai assumir qualquer valor, dado o observado valores de atributo de Xnew e dadas as distribuições P(Y) e P(X|Y) estimada a partir dos dados de treinamento.
assim, como vamos prever a classe da variável resposta, com base nos diferentes valores que alcançamos para P(Y|X)., Nós simplesmente tomamos o mais provável ou máximo destes valores. Portanto, este procedimento também é conhecido como maximização a posteriori.
maximizando a probabilidade
se assumirmos que a variável de resposta está uniformemente distribuída, ou seja, é igualmente provável obter qualquer resposta, então podemos simplificar ainda mais o algoritmo. Com esta suposição o a priori ou P(Y) torna-se um valor constante, que é 1/categorias da resposta.
As, the priori and evidence are now independent of the response variable, these can be removed from the equation., Portanto, a maximização a posteriori é reduzida para maximizar o problema da probabilidade.
distribuição de recursos
conforme visto acima, precisamos estimar a distribuição da variável de resposta a partir do conjunto de treinamento ou assumir distribuição uniforme. Da mesma forma, para estimar os parâmetros para a distribuição de uma característica, deve-se assumir uma distribuição ou gerar modelos não paramétricos para as características do conjunto de treinamento. Tais pressupostos são conhecidos como modelos de eventos. As variações nestes pressupostos geram algoritmos diferentes para fins diferentes., Para distribuições contínuas, as Bayes ingênuas Gaussianas são o algoritmo de escolha. Para características discretas, distribuições multinomiais e Bernoulli como populares. A discussão detalhada destas variações está fora do âmbito deste artigo.os classificadores ingênuos de Bayes funcionam muito bem em situações complexas, apesar das suposições simplificadas e ingenuidade. A vantagem destes classificadores é que necessitam de um pequeno número de dados de formação para estimar os parâmetros necessários para a classificação. Este é o algoritmo de escolha para categorização de texto., Esta é a ideia básica por trás dos Classificadores ingênuos do Bayes, que você precisa começar a experimentar com o algoritmo.