Esta página examina as propriedades tridimensionais ou ‘sólida’ formas.
uma forma bidimensional tem comprimento e largura. Uma forma sólida tridimensional também tem profundidade. Formas tridimensionais, pela sua natureza, têm um interior e um exterior, separados por uma superfície. Todos os itens físicos, coisas em que se pode tocar, são tridimensionais.,
esta página cobre ambos os sólidos de lados retos chamados poliedros, que são baseados em polígonos, e sólidos com curvas, tais como globos, cilindros e cones.
poliedros
poliedros (ou poliedros) são formas sólidas rectas. Os poliedros são baseados em polígonos, formas planas bidimensionais com linhas retas.
veja as propriedades da nossa página de polígonos para mais informações sobre o trabalho com polígonos.
poliedros são definidos como tendo:
- arestas rectas.lados planos chamados faces.,
- cantos, chamados vértices.
poliedros também são muitas vezes definidos pelo número de arestas, faces e vértices que têm, bem como se suas faces são todas da mesma forma e tamanho. Como os polígonos, os polígonos podem ser regulares (baseados em polígonos regulares) ou irregulares (baseados em polígonos irregulares). Poliedros também podem ser côncavos ou convexos.
Um dos poliedros mais básicos e familiares é o cubo. Um cubo é um poliedro regular, com seis faces quadradas, 12 arestas e oito vértices.,

Poliedros Regulares (Sólidos Platónicos)
Os cinco sólidos regulares são uma classe especial de poliedros, cujos rostos são idênticos, com cada cara de ser um polígono regular. Os sólidos platónicos são:
- tetraedro com quatro faces triangulares equiláteras.cubo com seis faces quadradas.octaedro com oito faces triangulares equiláteras.Dodecaedro com doze faces do Pentágono.Icosaedro com vinte faces triangulares equiláteras.,
ver o diagrama acima para uma ilustração de cada um destes poliedros regulares.
o que é um prisma?
um prisma é qualquer poliedro que tem duas extremidades correspondentes e lados planos. Se você cortar um prisma em qualquer lugar ao longo de seu comprimento, paralelo a uma extremidade, sua seção transversal é a mesma-você acabaria com dois prismas. Os lados de um prisma são paralelos – formas de quatro lados com dois pares de lados com igual comprimento.os Antiprismas são semelhantes aos prismas regulares, as suas extremidades coincidem., No entanto, os lados dos anti-prismas são constituídos por triângulos e não paralelos. Os antiprismas podem tornar-se muito complexos.o que é uma pirâmide?
uma pirâmide é um poliedro com uma base de polígono que se conecta a um vértice (ponto superior) com lados retos.embora tendamos a pensar em pirâmides com uma base quadrada, como as que os antigos egípcios construíram, eles podem de fato ter qualquer base poligonal, regular ou irregular. Além disso, uma pirâmide pode ter um ápice no centro direto de sua base, uma pirâmide direita, ou pode ter o ápice fora do centro quando é uma pirâmide oblíqua.,
poliedros mais complexos
Existem muitos mais tipos de poliedros: simétricos e assimétricos, côncavos e convexos. os sólidos Arquimedeanos, por exemplo, são constituídos por pelo menos dois polígonos regulares diferentes.
o cubo truncado (como ilustrado) é um sólido Arquimedeano com 14 faces. 6 das faces são octágonos regulares e os outros 8 são triângulos regulares (equiláteros). A forma tem 36 arestas e 24 vértices (cantos).,
formas tridimensionais com curvas
formas sólidas que incluem uma aresta curva ou redonda não são poliedros. Os poliedros só podem ter lados retos.
muitos dos objectos à sua volta irão incluir pelo menos algumas curvas. Em Geometria, os sólidos curvos mais comuns são cilindros, cones, esferas e tori (plural para torus).,
Common Formas Tridimensionais com Curvas: Cilindro Cone Um cilindro tem a mesma seção transversal de um lado para o outro. Os cilindros têm duas extremidades idênticas de um círculo ou oval. Embora semelhantes, os cilindros não são prismas, pois um prisma tem (por definição) paralelogramo, lados planos.,um cone tem uma base circular Ou oval e um vértice (ou vértice). O lado do cone desliza suavemente para o ápice. Um cone é semelhante a uma pirâmide, mas distinto como um cone tem um único lado curvado e uma base circular. Esfera Toro a Forma de uma bola ou de um globo, uma esfera é um objeto redondo. Cada ponto na superfície de uma esfera é uma distância igual ao centro da esfera., em forma de anel, pneu ou donut, um toro de anel regular é formado por girar um círculo menor em torno de um círculo maior. Existem também formas mais complexas de tori. superfície
a nossa página Sobre a área de cálculo explica como trabalhar a área de formas bidimensionais e você precisa de compreender estes conceitos básicos para calcular a área de superfície de formas tridimensionais.para formas tridimensionais, falamos de área de superfície, para evitar confusão.,
Você pode usar o seu conhecimento sobre a área de formas bidimensionais para calcular a área de superfície de uma forma tridimensional, UMA vez que cada face ou lado é efetivamente uma forma bidimensional.portanto, você determina a área de cada face, e depois adiciona-as juntas.tal como com formas planas, a superfície de um sólido é expressa em unidades quadradas: cm2, inches2, m2 e assim por diante. Você pode encontrar mais detalhes sobre Unidades de medida em nossos sistemas de medição página.,
Exemplos de Cálculos de Área de Superfície
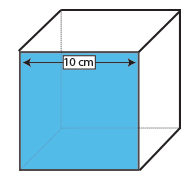
Cubo
A área da superfície de um cubo é a área de uma face (comprimento x largura) multiplicado por 6, porque todas as seis faces são iguais.
Como a face de um cubo é um quadrado, você só precisa tomar uma medida – o comprimento e a largura de um quadrado são, por definição, o mesmo.
uma face deste cubo é, portanto, 10 × 10 cm = 100cm2. Multiplique por 6, O número de faces em um cubo, e descobrimos que a área de superfície deste cubo é de 600cm2.,
Outros Poliedros Regulares
da mesma forma, a área de superfície de outros poliedros regulares (sólidos platónicos) pode ser trabalhado por encontrar a área de um lado e, em seguida, multiplicando-se a resposta pelo número total de lados – ver Básico Poliedros diagrama acima.se a área de um pentágono que compõe um dodecaedro for 22cm2, multiplique isso pelo número total de lados (12) para dar a resposta 264cm2.,
pirâmide
para calcular a superfície de uma pirâmide padrão com quatro lados triangulares iguais e uma base quadrada:
primeiro, calcular a área do comprimento da base (Quadrado) × Largura.em seguida, defina a área de um lado (triângulo). Medir a largura ao longo da base e, em seguida, a altura do triângulo (também conhecido como comprimento inclinado) a partir do ponto central na base para o ápice.,
pode então dividir a sua resposta por 2 para lhe dar a área de superfície de um triângulo e depois multiplicar por 4 para dar a área de superfície de todos os quatro lados, ou simplesmente multiplicar a área de superfície de um triângulo por 2.
finalmente adicione a área da base e os lados juntos para encontrar a área total da superfície da pirâmide.
para calcular a área de superfície de outros tipos de pirâmide, adicione a área da base (conhecida como área de base) e a área dos lados (área lateral), você pode precisar medir os lados individualmente.,
diagramas líquidos
uma rede geométrica é um “padrão” bidimensional para um objeto tridimensional. As redes podem ser úteis quando se trabalha a área de superfície de um objeto tridimensional. No diagrama abaixo você pode ver como pirâmides básicas são construídas, se a pirâmide é ‘desdobrada’ você fica com a rede.
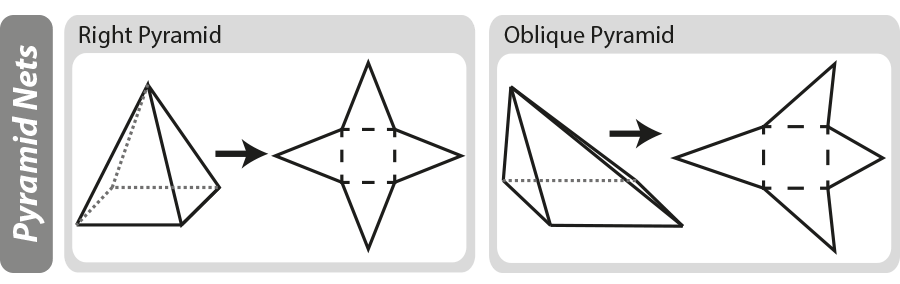
Para mais em diagramas de Rede, Veja as nossas páginas 3D formas e Redes.

Prism
para calcular a área de superfície de um prisma:
prismas têm duas extremidades os mesmos lados do paralelogramo plano.,
Calcule a área de uma extremidade e multiplique por 2.
para um prisma regular (onde todos os lados são os mesmos) calcule a área de um dos lados e multiplique pelo número total de lados.para prismas irregulares (com lados diferentes) calcule a área de cada lado.
adicione as suas duas respostas juntas (extremidades × lados) para encontrar a área total da superfície do prisma.,
Cilindro

Exemplo:
Radius = 5cm
Altura = 10 cmPara calcular a área da superfície de um cilindro, é útil pensar sobre o componente partes da forma. Imagine uma lata de milho doce-tem um topo e um fundo, ambos são círculos. Se você cortar o lado ao longo de seu comprimento e achatá-lo, você teria um retângulo. Portanto, você precisa encontrar a área de dois círculos e um retângulo.
primeiro trabalhar a área de um dos círculos.
a área de um círculo É π (pi) × radius2.,
assumindo um raio de 5cm, a área de um dos círculos é de 3.14 × 52 = 78.5cm2.
multiplique a resposta por 2, uma vez que existem dois círculos 157cm2
A área do lado do cilindro é o perímetro do círculo × a altura do cilindro.
O perímetro é igual a π x 2 × raio. No nosso exemplo, 3.14 × 2 × 5 = 31.4
medir a altura do cilindro – por exemplo, a altura é de 10cm. A área de superfície do lado é de 31.4 × 10 = 314cm2.,
O total de área de superfície pode ser encontrada adicionando a área dos círculos e o lado:
157 + 314 = 471cm2

Exemplo:
Radius = 5cm
Comprimento de Inclinação = 10 cmCone
Quando o cálculo da área da superfície de um cone que você precisa para usar o comprimento da ‘inclinação’, bem como o raio da base.
no entanto, é relativamente simples calcular:
a área do círculo na base do cone É, π(pi) × radius2.
neste exemplo, a soma é 3.14 × 52 = 3.14 × 25 = 78.,5cm2
a área do lado, a secção inclinada, pode ser encontrada usando esta fórmula:
π(pi) × raio × comprimento da inclinação.
no nosso exemplo, a soma é de 3.14 × 5 × 10 = 157cm2.finalmente adicione a área de base à área lateral para obter a área total da superfície do cone.
a 78,5 + 157 = 235.5cm2

Bola de Tênis:
Diâmetro = 2,6 polegadasEsfera
A área de superfície de uma esfera é relativamente simples expansão da fórmula para um círculo de área.
4 × π × radius2.,
para uma esfera é frequentemente mais fácil medir o diâmetro-a distância através da esfera. Você pode então encontrar o raio que é metade do diâmetro.
O diâmetro de uma bola de tênis padrão é de 2,6 polegadas. O raio é, portanto, de 1,3 polegadas. Para a fórmula, precisamos do raio ao quadrado. 1.3 × 1.3 = 1.69.
A superfície de uma bola de ténis é, portanto:
4 × 3.14 × 1.69 = 21.2264 inches2.,

Exemplo:
R (Raio Grande) = 20 cm
r (Raio Pequeno) = 4 cmToro
para calcular a área da superfície de um toro você precisa encontrar duas raio de valores.
o raio maior ou grande (R) é medido do meio do buraco até o meio do anel.
o raio pequeno ou menor (r) é medido do meio do Anel até à aresta exterior.
O diagrama mostra duas vistas de um toro de exemplo e como medir os seus raios (ou raios).,
o cálculo para encontrar a área de superfície está em duas partes (uma para cada raio). O cálculo é o mesmo para cada parte.
a fórmula é: área de superfície = (2nR) (2nr)
para trabalhar a área de superfície do toro exemplo.
(2 × π × R) = (2 × 3.14 × 20) = 125.6
(2 × π × r) = (2 × 3.14 × 4) = 25.12
multiplique as duas respostas juntas para encontrar a área total da superfície do toro exemplo.