znajdowanie funkcji kwadratowych dla podanych paraboli – Funkcje kwadratowe

znajdowanie funkcji kwadratowych dla podanych paraboli

istnieje tak wiele różnych rodzajów problemów, które można zadać w odniesieniu do równań kwadratowych. W tym artykule skupimy się na tym, jak możemy opracować równanie kwadratowe z grafu kwadratowego za pomocą kilku różnych metod., Ale zanim przejdziemy do tego typu problemów, poświęć chwilę, aby pobawić się wyrażeniami kwadratowymi na tym wspaniałym kalkulatorze graficznym online tutaj. Im wygodniej posługujesz się wykresami kwadratowymi i wyrażeniami, tym łatwiej będzie Ci ten temat!

teraz przejdźmy do rozwiązywania problemów z tą wiedzą, a mianowicie, jak znaleźć równanie paraboli!

jak znaleźć Równanie kwadratowe z grafu:

aby znaleźć równanie kwadratowe z grafu, są dwie proste metody, które można zastosować: używając 2 punktów lub używając 3 punktów.,

1) Znajdź Równanie kwadratowe z 2 punktów

aby znaleźć równanie kwadratowe z grafu używającego tylko 2 punktów, jednym z tych punktów musi być wierzchołek. Z wierzchołkiem i jednym innym punktem, możemy podłożyć te współrzędne do tego, co nazywa się „formą wierzchołka”, a następnie rozwiązać nasze równanie., Wzór wierzchołka jest następujący, gdzie (d,f) jest punktem wierzchołka i (x,y) jest drugim punktem:

(y±D)=a(x±f)2(y \pm D) = A(x \pm f)^{2}(y±D)=A(x±F)2

forma wierzchołkowa może być również zapisana w bardziej „właściwej” formie, jako:

y=a(x±f)2∓dy = a(X \PM f)^{2} \MP dy=a(x±f)2∓D

używając tej formuły, wszystko, co musimy zrobić, to sub w wierzchołek i drugi punkt, rozwiązać dla a, a następnie przepisać nasze ostateczne równanie., Najlepszym sposobem na komfortowe korzystanie z tego formularza jest zrobienie przykładowego problemu z nim.

przykład:

Określ równanie paraboli pokazane na poniższym obrazku.

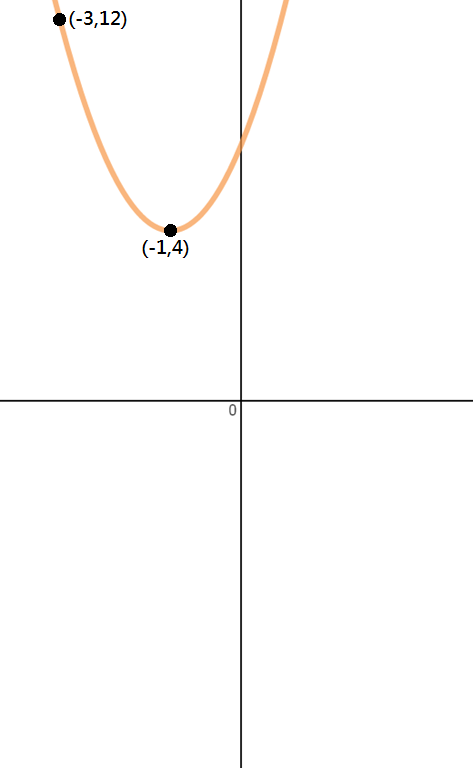
Krok 1: Zidentyfikuj punkty

ponieważ mamy tylko dwa punkty w tabeli.ten problem, wierzchołek i inny punkt, musimy użyć formy wierzchołka, aby rozwiązać to pytanie.,

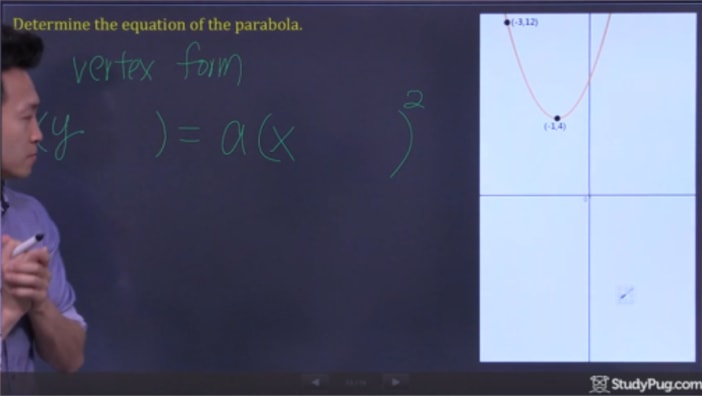
Krok 2: podpunkty do formularza wierzchołka i rozwiąż dla „a”

teraz wszystko co musimy zrobić to sub w naszych dwóch punktach do wzoru wierzchołkowego i rozwiązać dla „a”, aby mieć wszystkie informacje do napisania naszego ostatecznego równania kwadratowego.,4) = a(-3+1)2(12 – 4) = a(-3 + 1)^{2}(12-4)=a(-3+1)2

8=a(-2)28 = a(-2)^{2}8=a(-2)28=4A8 = 4A8=4Aa=2a = 2a=2

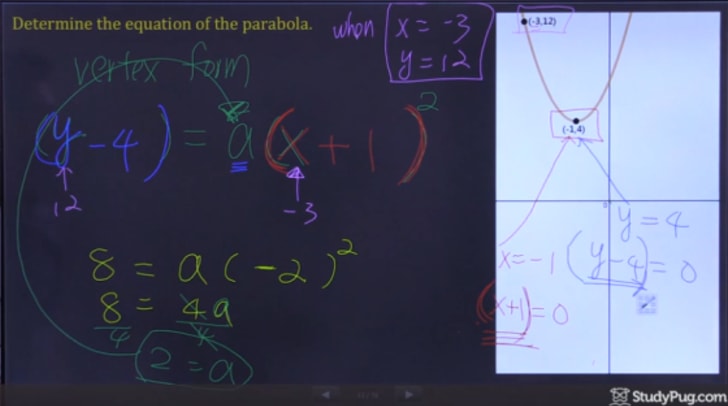
krok 3: napisz równanie kwadratowe

po rozwiązaniu dla „a”, mamy teraz wszystkie informacje potrzebne do napisania naszej ostatecznej odpowiedzi.,

y−4=2(x+1)2Y – 4 = 2(x + 1)^{2}y−4=2(x+1)2

a następnie, w odpowiedniej formie wierzchołka paraboli, nasza ostateczna odpowiedź brzmi:

y=2(x+1)2+4Y = 2(x + 1)^{2} + 4Y=2(x+1)2+4

to kończy lekcję o postaci wierzchołków i jak znaleźć równanie kwadratowe z 2 punktów!, Jeśli chcesz odświeżyć swoją pamięć na Pokrewne tematy, takie jak rozwiązywanie wyrażeń kwadratowych w formie wierzchołków, jak konwertować regularne równanie kwadratowe ze standardowego formularza do postaci wierzchołków poprzez wypełnienie kwadratu i jak używać formuły wierzchołków, sprawdź nasze lekcje.

2) Znajdź Równanie kwadratowe z 3 punktów

w niektórych przypadkach nie będziemy mieć tyle szczęścia, aby otrzymać punkt na wierzchołku. Jeśli tak jest, nie możemy już znaleźć wyrażenia kwadratowego za pomocą tylko dwóch punktów i musimy zrobić coś nieco innego., W przypadku, gdy otrzymamy informacje o X-przechwytach paraboli, a także o jednym innym punkcie, możemy znaleźć równanie kwadratowe za pomocą równania, które nazywa się „formularzem faktorowanym”. Ogólne równanie dla wzoru formula_1 jest następujące, przy czym B I c są wartościami współrzędnych X X przechwytów:

y=a(x-b)(x-c)y = a(x−b)(x−C)

używając tego wzoru, wystarczy, że podamy współrzędne X – X – X−X−X-X-X-X-X-X-X-X-X-X-X-X-X-X-X-X-X-X-X-X-X-X-X-X-X-X-X-X-X-X., Ponownie, najlepszym sposobem, aby uzyskać komfort z tej postaci równań kwadratowych jest zrobić przykładowy problem.

przykład:

Określ równanie paraboli pokazane na poniższym obrazku:

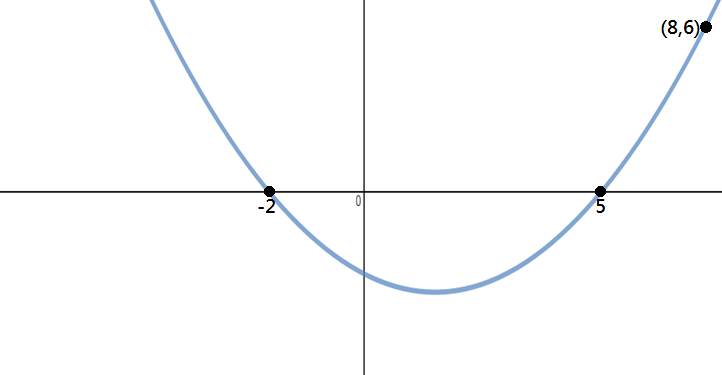
krok 1: Zidentyfikuj punkty

ponieważ otrzymujemy trzy punkty w tym problemie, x-przechwyty i inny punkt, możemy użyć formularza factored do rozwiązania tego pytania.,

z wykresu widać, że X-2 i 5, a punkt na paraboli to (8,6).

Krok 2: podpunkty do postaci wierzchołkowej i rozwiąż dla „a”

teraz wszystko, co musimy zrobić, to sub w naszych wartościach do Formuły formula_1 i rozwiąż dla „a”, aby mieć wszystkie informacje do napisania naszego ostatecznego równania kwadratowego.,(x-5)y=(x+2) (x−5)

następnie możemy użyć punktu na paraboli (8,6) do rozwiązania dla „a”:

6=a(8+2)(8-5)6 = a(8 + 2)(8 – 5)6=a(8+2)(8-5)6=a(10)(3)6 = a(10)(3)6=a(10)(3)6=30a6 = 30a6=30Aa=15A = \frac{1}{5}a=51

Krok 3: Zapisz równanie kwadratowe

po rozwiazaniu dla „a” mamy teraz wszystkie informacje potrzebne do napisania naszej ostatecznej odpowiedzi.,

y=15(x+2)(x−5)y = \frac{1}{5} (x + 2)(x – 5)y=51(x+2)(x−5)

i to wszystko! Są to dwie najważniejsze metody znajdowania funkcji kwadratowej z danej paraboli. Aby uzyskać dalsze badania nad funkcjami kwadratowymi i ich wykresami, zapoznaj się z tymi przydatnymi filmami zajmującymi się dyskryminacją, wykresami nierówności kwadratowych i sekcjami stożkowymi.