
krótkie wyjaśnienie i dowód
racjonalne twierdzenie o korzeniu (RRT) jest przydatnym narzędziem do swojego arsenału matematycznego. Zapewnia szybki i brudny test na racjonalność niektórych wyrażeń. I pomaga znaleźć racjonalne korzenie wielomianów.,
oto jak i dlaczego to działa.,e53714″>
jak
Załóżmy, że masz wielomian stopnia n, ze współczynnikami całkowitymi:

twierdzenie o racjonalnym korzeniu mówi: jeśli istnieje racjonalny korzeń, to jego składniki podzielą pierwszy i ostatni współczynnik:
racjonalny korzeń jest wyrażony w najniższych wartościach., Oznacza to, że p i q nie mają wspólnych czynników. (To będzie ważne później.) Licznik dzieli stałą na końcu wielomianu; demominator dzieli współczynnik wiodący.
jako przykład:
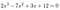
musimy tylko spojrzeć na 2 i 12.,:
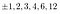
The factors of 2:
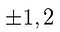
Thus, if a rational root does exist, it’s one of these:
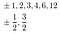
Plug each of these into the polynomial., Which one(s) — if any solve the equation? If none do, there are no rational roots.
Are any cube roots of 2 rational? A rational root, p/q must satisfy this equation.
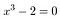
Furthermore:
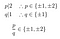
Not one of these candidates qualifies., Przejdź do:
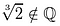
dlaczego
wróćmy jeszcze raz do naszego paradygmatu wielomianu.,

Scoot the constant to the other side:

Now, plug in our rational root, p/q.,

należy pomnożyć wszystko na qⁿ:

za każdym okresie, z lewej i n w ogólne. Weź to pod uwagę.,

wygląda o wiele gorzej niż musi być. Wymieńmy to wszystko w nawiasie na s. nie obchodzi nas, co tam jest.
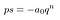
to o wiele łatwiejsze dla oczu.
pamiętaj, że p i q są liczbami całkowitymi. Nie mają też wspólnych czynników., Dlatego p nie może dzielić qⁿ. Powinien podzielić a₀:
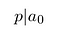
wróćmy teraz do naszego wielomianu paradygmatu:

tym razem zły pierwszy człon po prawej stronie.,

Insert the rational root:

As before, multiply by qⁿ.

This time, the common factor on the left is q., Let’s extract it, and lump together the remaining sum as t.
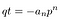
Again, q and p have no common factors. Therefore:
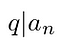
Thus proves the rational root theorem.