twierdzenie Bayesa znajduje wiele zastosowań w teorii prawdopodobieństwa i statystyce. Istnieje mikro szansa, że nigdy w życiu nie słyszałeś o tym twierdzeniu. Okazuje się, że to twierdzenie znalazło się w świecie uczenia maszynowego, tworząc jeden z wysoko zdobionych algorytmów. W tym artykule dowiemy się wszystkiego o naiwnym algorytmie Bayesa, wraz z jego odmianami do różnych celów w uczeniu maszynowym.
jak można się domyślić, wymaga to od nas patrzenia na rzeczy z probabilistycznego punktu widzenia., Podobnie jak w uczeniu maszynowym, mamy atrybuty, zmienne odpowiedzi i przewidywania lub klasyfikacje. Korzystając z tego algorytmu, będziemy mieli do czynienia z rozkładami prawdopodobieństwa zmiennych w zbiorze danych i przewidywania prawdopodobieństwa zmiennej odpowiedzi należącej do określonej wartości, biorąc pod uwagę atrybuty nowej instancji. Zacznijmy od przeglądu twierdzenia Bayesa.
twierdzenie Bayesa
To pozwala nam zbadać prawdopodobieństwo zdarzenia na podstawie wcześniejszej wiedzy o każdym zdarzeniu, które związane jest z poprzednim zdarzeniem., Tak więc na przykład prawdopodobieństwo, że cena domu jest wysoka, można lepiej ocenić, jeśli znamy obiekty wokół niego, w porównaniu do oceny dokonanej bez znajomości lokalizacji domu. Twierdzenie Bayesa robi dokładnie to.

div id=”7d5210017b”>
powyższe równanie daje podstawową reprezentację twierdzenia Bayesa., Tutaj A i B są dwa zdarzenia i,
P (A / B): prawdopodobieństwo warunkowe, że zdarzenie A wystąpi , biorąc pod uwagę, że B miało miejsce. Jest to również znane jako prawdopodobieństwo tylne.
p(A) i P(B) : prawdopodobieństwo A i B bez względu na siebie.<|p>
P(B / A) : warunkowe prawdopodobieństwo wystąpienia zdarzenia B, biorąc pod uwagę, że A miało miejsce.
teraz zobaczmy, jak to dobrze pasuje do celu uczenia maszynowego.,
Weźmy prosty problem uczenia maszynowego, w którym musimy nauczyć się naszego modelu z danego zestawu atrybutów(w przykładach treningowych), a następnie utworzyć hipotezę lub relację do zmiennej odpowiedzi. Następnie używamy tej relacji do przewidywania odpowiedzi, biorąc pod uwagę atrybuty nowej instancji. Korzystając z twierdzenia Bayesa, możliwe jest zbudowanie ucznia, który przewiduje prawdopodobieństwo zmiennej odpowiedzi należącej do jakiejś klasy, biorąc pod uwagę nowy zestaw atrybutów.
rozważmy jeszcze raz poprzednie równanie. Załóżmy, że A jest zmienną odpowiedzi, A B jest atrybutem wejściowym., Więc zgodnie z równaniem mamy
P(A|B) : warunkowe prawdopodobieństwo zmiennej odpowiedzi należącej do określonej wartości, biorąc pod uwagę atrybuty wejściowe. Jest to również znane jako prawdopodobieństwo tylne.
P (A): wcześniejsze prawdopodobieństwo zmiennej odpowiedzi.
P(B): prawdopodobieństwo danych treningowych lub dowodów.
P(B|A) : jest to znane jako prawdopodobieństwo danych treningowych.,
dlatego powyższe równanie można przepisać jako
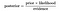
weźmy problem, w którym liczba atrybutów jest równa n, a odpowiedź jest wartością logiczną, tzn. może być w jednej z dwóch klas. Również atrybuty są kategoryczne (2 kategorie dla naszego przypadku). Teraz, aby wytrenować klasyfikator, będziemy musieli obliczyć P (B / A) dla wszystkich wartości w przestrzeni instancji i odpowiedzi., Oznacza to, że będziemy musieli obliczyć 2*(2^n -1), parametry do nauki tego modelu. Jest to ewidentnie nierealistyczne w większości dziedzin praktycznego uczenia się. Na przykład, jeśli jest 30 atrybutów logicznych, to będziemy musieli oszacować ponad 3 miliardy parametrów.
naiwny algorytm Bayesa
złożoność powyższego klasyfikatora bayesowskiego musi zostać zmniejszona, aby była praktyczna. Naiwny algorytm Bayesa robi to, przyjmując założenie warunkowej niezależności nad zestawem danych treningowych. To drastycznie zmniejsza złożoność wyżej wymienionego problemu do zaledwie 2n.,
założenie warunkowej niezależności stwierdza, że biorąc pod uwagę zmienne losowe X, Y i Z, mówimy, że X jest warunkowo niezależne od Y podanej Z, wtedy i tylko wtedy, gdy rozkład prawdopodobieństwa rządzący X jest niezależny od wartości Y podanej Z.
innymi słowy, X i Y są warunkowo niezależne podaną Z wtedy i tylko wtedy, gdy, biorąc pod uwagę, że z występuje, wiedza o tym, czy X występuje, nie dostarcza informacji o prawdopodobieństwie wystąpienia y, a wiedza o tym, czy y występuje, nie dostarcza informacji o prawdopodobieństwie wystąpienia X.,
to założenie sprawia, że algorytm Bayesa jest naiwny.
biorąc pod uwagę, n różnych wartości atrybutów, prawdopodobieństwo można teraz zapisać jako
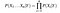
tutaj X reprezentuje atrybuty lub cechy, a y jest zmienną odpowiedzi. Teraz P (X|Y) staje się równy iloczynowi, rozkładu prawdopodobieństwa każdego atrybutu x danego Y.,
maksymalizacja a Posteriori
to, co nas interesuje, to znalezienie prawdopodobieństwa tylnego lub P(Y|X). Teraz, dla wielu wartości Y, będziemy musieli obliczyć to wyrażenie dla każdego z nich.
biorąc pod uwagę nową instancję Xnew, musimy obliczyć prawdopodobieństwo, że Y przyjmie dowolną wartość, biorąc pod uwagę obserwowane wartości atrybutów Xnew i biorąc pod uwagę rozkłady P(Y) I P (X|Y) oszacowane na podstawie danych treningowych.
tak więc, jak będziemy przewidywać klasę zmiennej odpowiedzi, na podstawie różnych wartości, które osiągniemy dla P (Y / X)., Po prostu bierzemy najbardziej prawdopodobną lub maksymalną z tych wartości. Dlatego procedura ta jest również znana jako maksymalizacja a posteriori.
maksymalizacja prawdopodobieństwa
jeśli założymy, że zmienna odpowiedzi jest równomiernie rozłożona, to znaczy, że jest ona równie prawdopodobna do uzyskania dowolnej odpowiedzi, to możemy dodatkowo uprościć algorytm. Przy takim założeniu priori lub P (Y) staje się wartością stałą, która wynosi 1 / kategorii odpowiedzi.
ponieważ priori i dowody są teraz niezależne od zmiennej odpowiedzi, można je usunąć z równania., Dlatego maksymalizacja posteriori jest zredukowana do maksymalizacji problemu prawdopodobieństwa.
rozkład funkcji
jak widać powyżej, musimy oszacować rozkład zmiennej odpowiedzi z zestawu treningowego lub założyć równomierny rozkład. Podobnie, aby oszacować parametry dla rozkładu funkcji, należy założyć dystrybucję lub wygenerować nieparametryczne modele dla funkcji z zestawu treningowego. Takie założenia są znane jako modele zdarzeń. Różnice w tych założeniach generują różne algorytmy do różnych celów., Dla rozkładów ciągłych algorytmem wyboru jest Gaussa naiwnego Bayesa. Dla funkcji dyskretnych popularne są rozkłady wielomianowe i Bernoulliego. Szczegółowe omówienie tych zmian nie wchodzi w zakres niniejszego artykułu.
naiwne klasyfikatory Bayesa sprawdzają się naprawdę dobrze w skomplikowanych sytuacjach, pomimo uproszczonych założeń i naiwności. Zaletą tych klasyfikatorów jest to, że wymagają one niewielkiej liczby danych treningowych do oszacowania parametrów niezbędnych do klasyfikacji. Jest to algorytm wyboru dla kategoryzacji tekstu., To jest podstawowa idea naiwnych klasyfikatorów Bayesa, że trzeba zacząć eksperymentować z algorytmem.