kształty trójwymiarowe: wielościany, krzywe bryły i powierzchnia

Ta strona bada właściwości kształtów trójwymiarowych lub brył.

dwuwymiarowy kształt ma długość i szerokość. Trójwymiarowy bryła ma również głębokość. Trójwymiarowe kształty, ze swej natury, mają wewnątrz i na zewnątrz, oddzielone powierzchnią. Wszystkie fizyczne przedmioty, rzeczy, których możesz dotknąć, są trójwymiarowe.,

ta strona obejmuje zarówno proste bryły zwane wielościanami, które są oparte na wielokątach, jak i bryły z krzywymi, takimi jak globusy, cylindry i stożki.

wielościany

wielościany (lub polyhedra) są prostostronnymi bryłami. Wielościany oparte są na wielokątach, dwuwymiarowych płaszczyznach o liniach prostych.

zobacz naszą stronę Właściwości wielokątów, aby dowiedzieć się więcej o pracy z wielokątami.

Polihedrony są zdefiniowane jako posiadające:

• proste krawędzie.
• płaskie boki zwane twarzami.,
• narożniki, zwane wierzchołkami.

wielościany są również często definiowane przez liczbę krawędzi, powierzchni i wierzchołków, które mają, a także czy ich twarze mają ten sam kształt i rozmiar. Podobnie jak wielokąty, wielościany mogą być regularne (oparte na wielokątach regularnych) lub nieregularne (oparte na wielokątach nieregularnych). Wielościany mogą być również wklęsłe lub wypukłe.

jednym z najbardziej podstawowych i znanych wielościanów jest sześcian. Sześcian jest regularnym wielościanem o sześciu kwadratowych powierzchniach, 12 krawędziach i ośmiu wierzchołkach.,

zwykłe wielościany (bryły platoniczne)

pięć stałych regularnych to specjalna klasa wielościanów, których wszystkie powierzchnie są identyczne, a każda powierzchnia jest regularnym wielokątem. Bryły platoniczne to:

• czworościan z czterema trójkątami równobocznymi.
• sześcian o sześciu kwadratowych powierzchniach.
• ośmiościan o ośmiu twarzach trójkąta równobocznego.
• Dodekahedron o dwunastu pentagonach twarzy.
• Ikosahedron z dwudziestoma trójkątami równobocznymi.,

Ilustracja każdego z tych zwykłych wielościanów znajduje się na powyższym diagramie.

Co to jest pryzmat?

pryzmat to dowolny wielościan, który ma dwa pasujące końce i płaskie boki. Jeśli wytniesz pryzmat w dowolnym miejscu wzdłuż jego długości, równolegle do końca, jego przekrój jest taki sam – skończysz z dwoma pryzmatami. Boki pryzmatu są równoległoboczne – czworoboczne kształty z dwiema parami boków o równej długości.

Antypryzmaty są podobne do zwykłych pryzmatów, ich końcówki pasują., Boki anty-pryzmatów składają się jednak z trójkątów, a nie paralelogramów. Antypryzmy mogą stać się bardzo złożone.

Co To jest piramida?

piramida jest wielościanem o podstawie wielokąta, który łączy się z wierzchołkiem (wierzchołkiem) o prostych bokach.

chociaż myślimy o piramidach o kwadratowej podstawie, takich jak te, które starożytni Egipcjanie zbudowali, w rzeczywistości mogą one mieć dowolną podstawę wielokąta, regularną lub nieregularną. Co więcej, piramida może mieć wierzchołek w bezpośrednim centrum swojej podstawy, prawą piramidę lub może mieć wierzchołek poza centrum, gdy jest to piramida ukośna.,

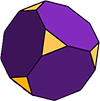
bardziej złożone wielościany

istnieje wiele innych rodzajów wielościanów: symetryczne i asymetryczne, wklęsłe i wypukłe.

bryły Archimedejskie, na przykład, składają się z co najmniej dwóch różnych wielokątów regularnych.

ścięta kostka (jak pokazano) jest bryłą Archimedejską o 14 twarzach. 6 z nich to ośmiokąty regularne, a pozostałe 8 to trójkąty równoboczne. Kształt ma 36 krawędzi i 24 wierzchołki (narożniki).,

trójwymiarowe kształty z krzywymi

bryły z zakrzywioną lub okrągłą krawędzią nie są wielościanami. Wielościany mogą mieć tylko proste boki.

wiele obiektów wokół ciebie będzie zawierać przynajmniej niektóre krzywe. W geometrii najczęściej zakrzywionymi bryłami są cylindry, stożki, kule i tori (liczba mnoga dla torus).,

wspólne trójwymiarowe kształty z krzywymi:
Cylinder	Stożek
cylinder ma taki sam przekrój poprzeczny od jednego końca do drugiego. Cylindry mają dwa identyczne końce okręgu lub owalu. Chociaż podobne, cylindry nie są pryzmatami, ponieważ pryzmat ma (z definicji) równoległobok, płaskie boki.,	stożek ma okrągłą lub owalną podstawę i wierzchołek (lub wierzchołek). Strona stożka zwęża się gładko do wierzchołka. Stożek jest podobny do piramidy, ale różni się od stożka ma pojedynczy zakrzywiony bok i okrągłą podstawę.
Kula	Torus
w kształcie kuli lub kuli kula jest całkowicie okrągły obiekt. Każdy punkt na powierzchni kuli jest jednakową odległością od środka kuli.,	w kształcie pierścienia, opony lub pączka, regularny pierścień powstaje przez obracanie mniejszego okręgu wokół większego okręgu. Istnieją również bardziej złożone formy tori.

Powierzchnia

nasza strona na temat obliczania powierzchni wyjaśnia, jak obliczyć powierzchnię kształtów dwuwymiarowych i musisz zrozumieć te podstawy, aby obliczyć powierzchnię kształtów trójwymiarowych.

w przypadku kształtów trójwymiarowych mówimy o powierzchni, aby uniknąć nieporozumień.,

możesz wykorzystać swoją wiedzę na temat powierzchni kształtów dwuwymiarowych do obliczenia powierzchni kształtu trójwymiarowego, ponieważ każda twarz lub strona jest w rzeczywistości kształtem dwuwymiarowym.

dlatego opracowujesz obszar każdej twarzy, a następnie dodajesz je razem.

podobnie jak w przypadku płaskich kształtów, pole powierzchni bryły wyraża się w jednostkach kwadratowych: cm2, inches2, m2 i tak dalej. Więcej szczegółów na temat jednostek miar znajdziesz na naszej stronie Systemy miar.,

przykłady obliczeń powierzchni

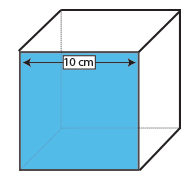
sześcian

powierzchnia sześcianu to powierzchnia jednej powierzchni (długość x szerokość) pomnożona przez 6, ponieważ wszystkie sześć powierzchni jest takich samych.

ponieważ powierzchnia sześcianu jest kwadratem, wystarczy wykonać tylko jeden pomiar – długość i szerokość kwadratu są z definicji takie same.

jedna powierzchnia tego sześcianu wynosi zatem 10 × 10 cm = 100cm2. Pomnóż przez 6, liczbę twarzy na sześcianie, a okaże się, że powierzchnia tego sześcianu wynosi 600cm2.,

Inne Polihedrony regularne

podobnie, pole powierzchni innych polihedronów regularnych (bryły platoniczne) można obliczyć, znajdując pole jednej strony, a następnie mnożąc odpowiedź przez całkowitą liczbę boków – patrz schemat podstawowych Polihedronów powyżej.

Jeśli powierzchnia jednego Pentagonu tworzącego dwunastościan wynosi 22cm2 to pomnóż to przez całkowitą liczbę boków (12), aby dać odpowiedź 264cm2.,

Piramida

aby obliczyć powierzchnię standardowej piramidy o czterech równych trójkątnych bokach i kwadratowej podstawie:

najpierw Oblicz powierzchnię podstawy (kwadratu) długość × szerokość.

następnie Oblicz obszar jednej strony (Trójkąt). Zmierz szerokość wzdłuż podstawy, a następnie wysokość trójkąta (znanego również jako długość skośna) od centralnego punktu na podstawie do wierzchołka.,

Możesz następnie podzielić odpowiedź przez 2, aby dać pole powierzchni jednego trójkąta, a następnie pomnożyć przez 4, aby dać pole powierzchni wszystkich czterech boków, lub po prostu pomnożyć pole powierzchni jednego trójkąta przez 2.

na koniec dodaj obszar podstawy i boków razem, aby znaleźć całkowitą powierzchnię piramidy.

aby obliczyć powierzchnię innych rodzajów piramid, dodaj razem obszar podstawy (znany jako obszar bazowy) i obszar boków (obszar boczny), może być konieczne zmierzenie boków indywidualnie.,

diagramy sieci

siatka geometryczna jest dwuwymiarowym 'wzorem' dla obiektu trójwymiarowego. Siatki mogą być pomocne przy ustalaniu powierzchni trójwymiarowego obiektu. Na poniższym diagramie możesz zobaczyć, jak zbudowane są piramidy podstawowe, jeśli piramida jest „rozwinięta”, pozostajesz z siecią.

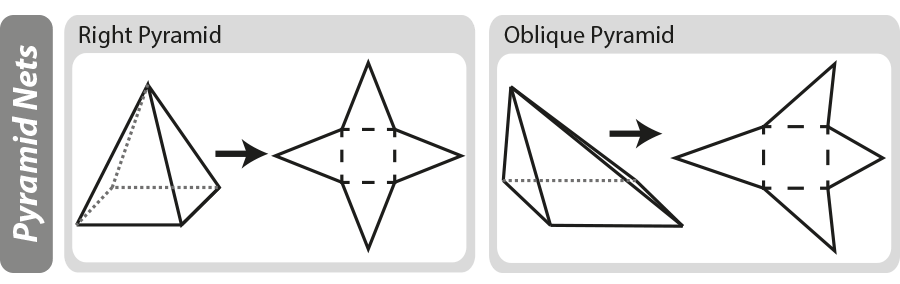
Więcej informacji na temat diagramów sieci znajdziesz na naszej stronie kształty i siatki 3D.

pryzmat

aby obliczyć pole powierzchni pryzmatu:

pryzmaty mają dwa końce o tych samych i płaskich bokach równoległoboku.,

Oblicz pole jednego końca i pomnóż przez 2.

dla zwykłego pryzmatu (gdzie wszystkie boki są takie same) Oblicz pole jednej ze stron i pomnóż przez całkowitą liczbę boków.

dla nieregularnych pryzmatów (o różnych bokach) Oblicz powierzchnię każdej strony.

Dodaj swoje dwie odpowiedzi razem (końce × boki), aby znaleźć całkowitą powierzchnię pryzmatu.,

Cylinder

aby obliczyć powierzchnię cylindra, warto pomyśleć o częściach składowych kształtu. Wyobraź sobie puszkę kukurydzy cukrowej – ma górę i dół, z których oba są kółkami. Jeśli wytniesz bok wzdłuż jego długości i spłacisz go, będziesz miał prostokąt. Dlatego musisz znaleźć obszar dwóch okręgów i prostokąta.

najpierw określ obszar jednego z kręgów.

powierzchnia okręgu wynosi π(pi) × promień2.,

zakładając promień 5cm, powierzchnia jednego z okręgów wynosi 3,14 × 52 = 78.5cm2.

pomnóż odpowiedź przez 2, ponieważ są dwa okręgi 157cm2

powierzchnia boku cylindra to Obwód okręgu × wysokość cylindra.

obwód jest równy π x 2 × promień. W naszym przykładzie, 3.14 × 2 × 5 = 31.4

zmierz wysokość cylindra – dla tego przykładu wysokość wynosi 10cm. Powierzchnia boku wynosi 31,4 × 10 = 314cm2.,

całkowitą powierzchnię można znaleźć dodając obszar okręgów i boku razem:

157 + 314 = 471cm2

Stożek

podczas obliczania powierzchni obszar stożka musisz użyć długości „skosu”, a także promienia podstawy.

jednak jest to stosunkowo proste do obliczenia:

pole okręgu u podstawy stożka wynosi π(pi) × promień2.

w tym przykładzie suma jest 3.14 × 52 = 3.14 × 25 = 78.,5cm2

pole boku, czyli pochyłej sekcji, można znaleźć za pomocą tego wzoru:

π(pi) × promień × długość pochyłej.

w naszym przykładzie suma wynosi 3.14 × 5 × 10 = 157cm2.

na koniec dodaj obszar bazowy do obszaru bocznego, aby uzyskać całkowitą powierzchnię stożka.

78.5 + 157 = 235.5cm2

Kula

Powierzchnia kuli jest stosunkowo prostym rozwinięciem wzoru na powierzchnię okręgu.

4 × π × radius2.,

dla sfery często łatwiej jest zmierzyć średnicę – odległość w poprzek kuli. Następnie można znaleźć promień, który jest połowę średnicy.

średnica standardowej piłki tenisowej wynosi 2,6 cala. Promień wynosi więc 1,3 cala. Dla wzoru potrzebujemy promienia kwadratowego. 1.3 × 1.3 = 1.69.

powierzchnia piłki tenisowej wynosi zatem:

4 × 3,14 × 1,69 = 21,2264 inches2.,

Torus

aby obliczyć powierzchnię torusa, musisz znaleźć dwie wartości promienia.

duży lub duży promień (R) mierzy się od środka otworu do środka pierścienia.

mały lub mały promień (r) jest mierzony od środka pierścienia do zewnętrznej krawędzi.

diagram pokazuje dwa widoki przykładowego toru i sposób pomiaru jego promieni (lub promieni).,

obliczanie powierzchni składa się z dwóch części (po jednej dla każdego promienia). Obliczenia są takie same dla każdej części.

wzór jest następujący: surface area = (2NR)(2NR)

aby obliczyć powierzchnię przykładowego torusa.

(2 × π × R) = (2 × 3.14 × 20) = 125.6

(2 × π × r) = (2 × 3.14 × 4) = 25.12

pomnóż obie odpowiedzi razem, aby znaleźć całkowitą powierzchnię przykładowego torusa.