Calculate Log & Antilog Online (Polski)

Mathematical Formulas

Calculating log (logbx):

logbx = y implies by = x.,

Where,

• b = base,
• y = number,
• x = log value.

Obliczanie Antylogu:

y = 10x

Gdzie,

• x = liczba,
• y = wartość antylogu.

logarytmy i anty-Logarytmy: Jak to działa i jego znaczenie

– Przewodnik autorstwa Corin B. Arenas, opublikowany w październiku 1, 2019

Jeśli kiedykolwiek zastanawiałeś się, jak eksperci określają wielkie odległości, intensywność trzęsień ziemi i globalne tempo wzrostu gospodarczego, to jesteś we właściwym miejscu.

Obliczanie bardzo dużych sum może być powolne i mylące., Ale za pomocą logarytmów (log) i antylogarytmów (antylog) obliczenia mogą być prostsze.

Czytaj dalej, aby dowiedzieć się więcej o logach i antylogach, jak działają i dlaczego są to istotne pojęcia matematyczne.

Co to jest Logarytm?

logarytm jest mocą, do której liczba (określana jako baza) musi zostać pomnożona do siebie, aby uzyskać daną liczbę. Mówiąc prościej, logarytm rozwiązuje problem:

ile razy mnożymy b, aby otrzymać kolejną liczbę y?,

Logarytm zlicza liczbę razy ten sam czynnik musi być pomnożony, aby uzyskać daną liczbę.

kto to wymyślił?

Log został wynaleziony w XVI wieku jako narzędzie obliczeniowe przez szkockiego matematyka, fizyka i astronoma, Johna Napiera. Napisał książkę Mirifici Logarithmorum Canonis Descriptio z tablicami i liczbami omawiającymi logarytmy naturalne, kładąc podwaliny pod jego podstawową koncepcję.

Napier ukuł termin logarytm z greckiego słowa logos, które oznacza „stosunek lub proporcję” i arytmos, który oznacza ” liczbę.,”Po połączeniu oznacza dosłownie” liczbę proporcji.”

2 typy logarytmów

logarytm naturalny liczby jest jej logarytmem do bazy stałej e, gdzie e jest w przybliżeniu równa 2.718281828459. Równanie zapisywane jest jako loge (x).

Jeśli logarytm nie określa podstawy, jak w tym przykładzie: log (1000), jest znany jako zwykły logarytm, który używa podstawy 10.

log(1000), jest znany jako wspólny logarytm, który wykorzystuje bazę 10.

Jak stosować Log?,

gdy zaczniesz obliczać liczby według milionów, miliardów i bilionów, może to być dość opodatkowane. Niezależnie od tego, czy chodzi o liczenie dużych pieniędzy, wzrost populacji, czy pokonywanie dużych odległości, log może pracować dla Ciebie. Może uprościć duże sumy, które wymagają długich i mylących równań, co ułatwia ich zrozumienie.

oto standardowe równanie loga:
logb(x) = y

Gdzie,

• liczba pomnożona przez siebie (b) jest bazą.
• liczba razy pomnożona (y) jest logarytmem.,
• uzyskana liczba (x) jest zapisywana w nawiasie.

aby zrozumieć, jak działa to pojęcie, oto przykład z mniejszą liczbą:
pytanie: Ile 2 mnożymy, aby otrzymać 32?
b = 2, x = 32

log2(32) = y
odpowiedź: 2 x 2 x 2 x 2 = 32

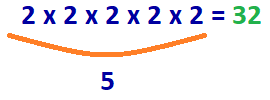
5 Liczba 2s musi zostać pomnożona, aby uzyskać liczbę 32.
odpowiedź: log2(32) = 5

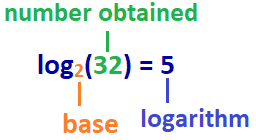
dlatego w tym przykładzie: logarytm 32 z bazą 2 wynosi 5, lub log 2 z bazy 32 wynosi 5.,

ponadto log jest odwrotną funkcją wykładniczą, gdzie operacja matematyczna zapisywana jest jako bn. b jest bazą, która jest mnożona zgodnie z mocą n, która jest liczbą razy jest mnożona dla siebie.

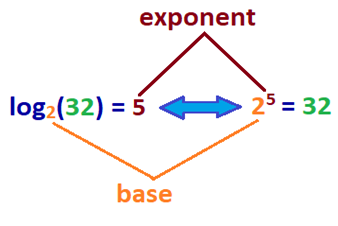
Co to oznacza? Log liczby jest wykładnikiem, do którego mnożona jest baza b w celu uzyskania danej liczby. Aby uzyskać lepszy pomysł, zapoznaj się z zestawem przykładowego równania dziennika wraz z poniższym równaniem wykładniczym.,

log	wykładnik
log2(32) = 5	25 = 32

teraz spróbujmy z dużą liczbą.
pytanie: Ile 10 mnożymy, aby otrzymać 150 000 000 000?
b = 10, x = 150 000 000 000

logb (x) = y
log(150 000 000 000) = y
y = 11.1760912590557
log(150 000 000 000) = 11.,1760912590557

rozwiązuje się to za pomocą funkcji log w kalkulatorze naukowym. Lub użyj kalkulatora na tej stronie, aby uzyskać odpowiedź.

W Jaki Sposób Antylogarytm ma związek z logiem?

numer dziennika może zostać zwrócony do jego oryginalnego numeru. Można to zrobić za pomocą antylogarytmu (antilogarithm). Tak więc antylog jest funkcją odwrotną loga. Podobnie, funkcja antylog służy do wykładniczego uproszczonej wartości dziennika.,

aby obliczyć antylog liczby y, musisz podnieść bazę logarytmu B (zwykle 10, czasami stałą e) do potęgi, która wygeneruje liczbę y.

oto równanie dla antylog z bazy 10:
10x = y
Gdzie X jest wykładnikiem, A y jest wartością antylog.

na przykład, jeśli weźmiemy to równanie log(5) = x, jego antylog będzie wynosił 10x = 5.

• Log: log(5) = 0.698970004336019
• Antlog: 100.698970004336019 = 5

teraz spróbujmy z większą liczbą.,

jeśli weźmiemy log(150,000,000,000) = x, jego antylog będzie wynosił 10x = 150,000,000,000.

• Log: log10(150,000,000,000) = 11.1760912590557
• Antylog: 1011.1760912590557= 150,000,000,000

znaczenie i rzeczywiste zastosowania

iv id przed wynalezieniem kalkulatorów, logarytmy były używane do upraszczania obliczeń w różnych dziedzinach wiedzy, takich jak nawigacja, Geodezja, Astronomia, a później Inżynieria.

wyobraź sobie żeglowanie na pustkowiu w XVI wieku., Nawigatorzy wówczas opierali się na położeniu gwiazd i mechanizmie sekstantu, aby określić ich dokładne położenie. Bez nowoczesnej technologii, która pomoże Ci obliczyć duże odległości, możesz użyć dziennika, aby uprościć obliczenia. Dokładność jest ważna, inaczej ryzykujesz więcej dni na morzu przy skromnych zapasach. Mniej równań oznacza mniej miejsca na błędy.

a co z innymi praktycznymi zastosowaniami? Nauka na żywo Stany logarytmy odnoszą progresje geometryczne do progresji arytmetycznych., Jeśli kiedykolwiek zauważyłeś powtarzające się kształty i wzory w naturze, architekturze i sztuce, te formacje posiadają własne odpowiadające im wartości logarytmiczne.

dzisiaj wiedza z tego, jak działają te wzory, wpływa na sposób, w jaki ludzkość konstruuje i projektuje domy, budynki i Miejskie krajobrazy.

Logarytmy są również używane do wyrażania zakresu i intensywności niektórych skal., Poza dużymi odległościami i dużymi prędkościami mierzy także inne rzeczy, takie jak:

• natężenie dźwięku
• częstotliwość dźwięku
• Siła burz wiatrowych
• Siła trzęsień ziemi
• poziom korozyjny kwasów
• twardość minerałów
• jasność gwiazd

weźmy za przykład decybele. Aby głośniki były głośniejsze o 10 decybeli, muszą być zasilane 10 razy większą mocą. Gdy zwiększysz go do +20 dB, będzie potrzebował 100 razy mocy, a o +30 dB będzie potrzebował 1000 mocy.

ponadto natężenie dźwięku postępuje arytmetycznie., Zmienia się również proporcjonalnie z logarytmem fali dźwiękowej, która postępuje geometrycznie.

Poniżej znajduje się tabela z żywej nauki z listą różnych skal logarytmicznych z odpowiadającymi im skalami liniowymi.

w pomiarach i rankingach

według Kalida Azada, nauczyciela matematyki za BetterExplained.com, logarytmy są tym, jak szybko coś rośnie.

logarytmy zwyczajowe zasadniczo opisują liczby w kategoriach ich potęg 10. Jeśli chodzi o stopę procentową, logarytm jest wzrost inwestycji.,

określając tempo wzrostu PKB danego kraju, analitycy dokonują przeglądu PKB w kolejnych latach. Biorą PKB z poprzedniego roku, a PKB z następnego roku, a następnie obliczają logarytm, aby znaleźć szacowaną stopę wzrostu.

Wyszukiwarki korzystają z wykresu linków, aby ocenić znaczenie, wiarygodność& PageRank Google był główną ewolucją w wyszukiwaniu, która zwiększyła Trafność wyszukiwania i pomogła Google search marketshare.,

według Azad, w skali od 1 do 10, Strona docelowa z PageRank 2 jest 10 razy bardziej popularna niż strona z PageRank 1. Jeśli strona ma PageRank 5, a strona konkurenta ma PageRank 9, to ma różnicę 4 rzędów wielkości.

rząd wielkości oznacza mniej więcej 10-krotną różnicę, lub ranking jest o 1 cyfrę większy w porównaniu z innymi. W tym przypadku strona z PageRank 9 jest o 100 000 000 bardziej popularna niż strona z PageRank 1.,

Dolna linia

Log i antylog to znaczące metody obliczeniowe, które pozwalają nam uprościć duże sumy. Uproszczenie skraca proces obliczeń i ułatwia ich zrozumienie. Pomaga to zmniejszyć miejsce na błędy.

Co więcej, korzystanie z log zapewnia mierzalne skale do pomiaru zjawisk naturalnych, takich jak intensywność trzęsień ziemi, Siła burz wiatrowych i jasność gwiazd. Jeśli chodzi o finanse, logarytmy pozwalają nam określić stopy procentowe i stopy wzrostu gospodarczego.

jest praktycznie stosowany w wielu dziedzinach., Duże wartości, które zależą od dokładności pomiaru, korzystają z obliczeń logarytmicznych.

o autorze

Corin jest zagorzałym badaczem i autorem tematów finansowych—bada trendy ekonomiczne, jak wpływają one na populacje, a także jak pomóc konsumentom w podejmowaniu mądrzejszych decyzji finansowych. Jej Inne artykuły można przeczytać na Inquirer.net oraz Manileno.com. posiada tytuł magistra w kreatywnym pisaniu na Uniwersytecie Filipin, jednej z najlepszych instytucji akademickich na świecie, i Licencjat w dziedzinie sztuki komunikacji z Miriam College.