
Sky & Telescoop
de meeste manieren om dingen te tellen en te meten werken logisch. Als het ding dat je meet toeneemt, wordt het getal groter. Als je zwaarder wordt, zegt de weegschaal je immers niet een kleiner aantal kilo ’s of kilo’ s. Maar dingen zijn niet zo verstandig in de astronomie — tenminste niet als het gaat om de helderheid van sterren., Voer het Magnitudesysteem in.
oude oorsprong van het Magnitudesysteem van sterren
stermagnituden tellen terug, het resultaat van een oude toevalstreffer die op dat moment een goed idee leek. Het verhaal begint rond 129 voor Christus, toen de Griekse astronoom Hipparchus de eerste bekende sterrencatalogus produceerde. Hipparchus rangschikte zijn sterren op een eenvoudige manier. Hij noemde de heldersten” van de eerste magnitude”, wat simpelweg “de grootste” betekent. Sterren die hij niet zo helder noemde van de tweede magnitude, of de tweede grootste. De zwakste sterren die hij kon zien noemde hij “van de zesde magnitude., Rond 140 na Christus kopieerde Claudius Ptolemaeus dit systeem in zijn eigen sterrenlijst. Soms voegde Ptolemaeus de woorden “groter” of “kleiner” toe om onderscheid te maken tussen sterren binnen een magnitudeklasse. Ptolemaeus ‘ werken bleven de basis astronomische teksten voor de volgende 1400 jaar, dus iedereen gebruikte het systeem van de eerste tot zesde magnitudes. Het werkte prima.
Galileo dwong de eerste verandering. Toen Galileo zijn nieuwe telescopen naar de hemel draaide, ontdekte hij dat er sterren bestonden die zwakker waren dan de zesde magnitude van Ptolemaeus., “Inderdaad, met het glas zult u onder sterren van de zesde magnitude zo’ n menigte van anderen ontdekken die aan het natuurlijke zicht ontsnappen dat het nauwelijks geloofwaardig is,” jubelde hij in zijn 1610 tract Sidereus Nuncius. “De grootste van deze . . . we kunnen het aanwijzen als van de zevende magnitude.”Zo kwam een nieuwe term in de astronomische taal, en het stellaire magnitude systeem werd open-ended. Er kan geen weg terug zijn.
naarmate telescopen groter en beter werden, bleven astronomen meer magnituden toevoegen aan de onderkant van de schaal., Vandaag zal een 50-millimeter verrekijker sterren laten zien van ongeveer 9 magnitude, een 6-inch amateurtelescoop zal bereiken tot 13 magnitude, en de Hubble Ruimtetelescoop heeft objecten gezien zo zwak als 31ste magnitude.in het midden van de 19e eeuw realiseerden astronomen zich dat er een dringende noodzaak was om de gehele schaal van het magnitudesysteem van de sterren nauwkeuriger te definiëren dan op basis van oogbal oordeel. Ze hadden al vastgesteld dat een 1ste magnitude ster schijnt met ongeveer 100 keer het licht van een 6de magnitude ster. Dienovereenkomstig, in 1856 de Oxford astronoom Norman R., Pogson stelde voor dat een verschil van vijf magnitudes precies gedefinieerd zou worden als een helderheidsverhouding van 100 tot 1. Deze handige regel werd snel aangenomen. Eén magnitude komt dus overeen met een helderheidsverschil van precies de vijfde wortel van 100, of heel dicht bij 2.512 — een waarde die bekend staat als de Pogson ratio.het resulterende stellaire magnitudesysteem is logaritmisch, in overeenstemming met het geloof uit de jaren 1850 dat alle menselijke zintuigen logaritmisch zijn in hun reactie op stimuli. De decibel schaal voor rating luidheid werd ook logaritmisch gemaakt.,
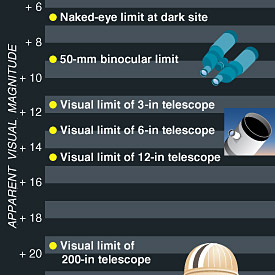
achtenvijftig magnitudes van schijnbare helderheid omvatten de dingen die astronomen bestuderen, van de stralende zon tot de zwakste objecten die met de Hubble-Ruimtetelescoop worden gedetecteerd. Dit bereik komt overeen met een helderheidsratio van ongeveer 200 miljard biljoen.
Sky & Telescope
helaas is het niet helemaal zo, niet voor helderheid, geluid of iets anders. Onze percepties van de wereld volgen krachtwetcurves, niet logaritmische. Dus een ster van magnitude 3.,0 ziet er in feite niet precies halverwege uit in helderheid tussen 2,0 en 4,0. Het ziet er wat zwakker uit. De ster die halverwege tussen 2,0 en 4,0 lijkt zal ongeveer magnitude 2,8 zijn. Hoe groter de magnitude kloof, hoe groter deze discrepantie. Dienovereenkomstig gebruikt Sky & de computergetekende hemelkaarten van de telescoop sterpunten die zijn aangepast aan een machtsverhouding.maar de wetenschappelijke wereld in de jaren 1850 was gaga voor logaritmen, dus nu zijn ze net zo stevig vastgezet in het magnitudesysteem van de sterren als Hipparchus ‘ achterwaartse nummering.,
nu stergrootheden op een precieze wiskundige schaal werden gerangschikt, hoe slecht passend ook, werd een ander probleem onvermijdelijk. Sommige “1e magnitude” sterren waren veel helderder dan andere. Astronomen hadden geen andere keuze dan de schaal uit te breiden naar helderdere en zwakke waarden. Rigel, Capella, Arcturus en Vega zijn dus magnitude 0, een onhandige uitspraak die klinkt alsof ze helemaal geen helderheid hebben! Maar het was te laat om opnieuw te beginnen. De magnitudeschaal strekt zich verder uit in negatieve getallen: Sirius schijnt met magnitude -1,5, Venus bereikt -4,4, de volle maan is ongeveer -12.,5, en de zon brandt met magnitude -26,7.
andere kleuren, Andere Magnitudes
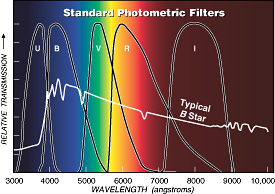
De bandpassen van de standaard UBVRI kleurfilters, samen met het spectrum van een typische blauw-witte ster.
Sky & Telescoop
door de late 19e eeuw gebruikten astronomen fotografie om de hemel vast te leggen en sterhelderheid te meten. Sommige sterren met dezelfde helderheid aan het oog toonden verschillende helderheid op film, en vice versa., In vergelijking met het oog waren fotografische emulsies gevoeliger voor blauw licht en minder voor rood licht. Dienovereenkomstig werden twee afzonderlijke schalen voor het magnitudesysteem van de sterren bedacht. Visuele magnitude, of MVIS, beschreef hoe een ster in het oog keek. Fotografische magnitude, of mpg, verwijst naar sterrenbeelden op blauw-gevoelige zwart-wit film. Deze zijn nu afgekort mv en mp, respectievelijk.
deze complicatie bleek een zegen in vermomming te zijn. Het verschil tussen de fotografische en visuele magnitude van een ster was een handige maat voor de kleur van de ster., Het verschil tussen de twee soorten magnitude werd de “kleurindex” genoemd.”De waarde ervan is steeds positiever voor gele, oranje en rode sterren, en negatief voor blauwe.
maar verschillende fotografische emulsies hebben verschillende spectrale reacties! En de ogen van mensen verschillen ook. Voor een ding, uw ooglenzen geel met de leeftijd; oude mensen zien de wereld door gele filters. Magnitude systemen ontworpen voor verschillende golflengtebereiken moesten duidelijker gedefinieerd worden dan dit.,
tegenwoordig worden precieze magnitudes bepaald door wat een standaard foto-elektrische fotometer ziet door middel van standaardkleurfilters. Verschillende fotometrische systemen zijn bedacht; de meest bekende wordt UBV genoemd naar de drie meest gebruikte filters. U omvat het bijna-ultraviolet, B is blauw en V komt vrij dicht overeen met de oude visuele magnitude; de brede piek ligt in de geel-groene band, waar het oog het gevoeligst is.
kleurindex is nu gedefinieerd als de magnitude B min de magnitude V. Een zuiver witte ster heeft een B-V van ongeveer 0,2, onze gele zon is 0.,63, oranje-rode Betelgeuse is 1,85, en de blauwste ster die mogelijk wordt geacht is -0,4, lichtblauw-wit.
het UBV-systeem was zo succesvol dat het werd uitgebreid met R-en I-filters om standaard rode en nabij-infrarode magnitudes te definiëren. Daarom wordt het ook wel UBVRI genoemd. Infraroodastronomen hebben het naar nog langere golflengten gedragen, die alfabetisch na I worden opgepikt om de J -, K -, L -, M -, N-en Q-banden te definiëren. Deze werden gekozen om overeen te komen met de golflengten van infrarood “vensters” in de atmosfeer van de aarde — golflengten waarbij waterdamp sterrenlicht niet volledig absorbeert.,
in alle golfbanden is de heldere ster Vega willekeurig gekozen om magnitude 0.0 te definiëren. Omdat Vega bij infraroodgolflengten dimmer is dan bij zichtbaar licht, zijn infraroodmagnituden per definitie en vrij kunstmatig “helderder” dan hun visuele tegenhangers.
uiterlijk en werkelijkheid
Wat is dan de werkelijke helderheid van een object? Hoeveel totale energie stuurt het naar ons op alle golflengten gecombineerd, zichtbaar en onzichtbaar? Het antwoord heet de bolometrische magnitude, mbol, omdat de totale straling ooit werd gemeten met een apparaat genaamd een bolometer., De bolometrische magnitude wordt het God ‘ s eye view van de ware glans van een object genoemd. Astrofysici waarderen het als de ware maat van de totale energie-emissie van een object gezien vanaf de aarde. De bolometrische correctie vertelt hoeveel helderder de bolometrische magnitude is dan de V magnitude. De waarde ervan is altijd negatief, omdat een ster of object ten minste enige straling uitzendt buiten het visuele gedeelte van het elektromagnetische spectrum.
tot nu toe hebben we alleen te maken gehad met schijnbare grootheden — hoe helder dingen eruit zien vanaf de aarde., We weten pas hoe helder een object is als we ook rekening houden met de afstand. Zo creëerden astronomen de absolute magnitudeschaal. De absolute magnitude van een object is gewoon hoe helder het zou lijken als het op een standaard afstand van 10 parsecs (32,6 lichtjaar) zou worden geplaatst.

op de linkerkaart van Canis Major geven de stipgroottes de schijnbare magnitudes van de sterren aan; de stippen komen overeen met de helderheid van de sterren zoals we ze zien., De rechter versie geeft de absolute magnitudes van dezelfde sterren aan-hoe helder ze zouden zijn als ze allemaal op dezelfde afstand (32,6 lichtjaar) van de aarde zouden zijn geplaatst. Absolute magnitude is een maat voor de ware sterlichtkracht.
Sky & Telescoop
gezien vanaf deze afstand zou de zon schijnen met een niet-indrukwekkende visuele magnitude 4,85. Rigel zou gloeien met een schitterende -8, bijna net zo helder als de kwartmaan. De rode dwerg Proxima Centauri, de ster die het dichtst bij het zonnestelsel staat, lijkt magnitude 15 te zijn.,6, de kleinste kleine glimmer zichtbaar in een 16-inch telescoop! Het kennen van absolute grootheden maakt duidelijk hoe enorm divers de objecten zijn die we terloops samenklonteren Onder het enkele woord “ster.”
Absolute magnitudes worden altijd geschreven met een hoofdletter M, schijnbare magnitudes met een kleine letter m. elk type schijnbare magnitudes-fotografisch, bolometrisch of wat dan ook-kan worden omgezet in een absolute magnitudes.
(voor kometen en asteroïden wordt een heel andere “absolute magnitude” gebruikt., De standaard hier is hoe helder het object zou lijken aan een waarnemer die op de zon staat als het object één astronomische eenheid verderop was.)
is het magnitudesysteem van de sterren te ingewikkeld? Geenszins. Het is gegroeid en geëvolueerd om elke behoefte aan helderheidsmeting precies te vullen zoals vereist. Hipparcus zou blij zijn.