Traagheidsmoment, algemene vorm
aangezien het traagheidsmoment van een gewoon object een continue verdeling van de massa omvat op een voortdurend wisselende afstand van elke rotatieas, omvat de berekening van traagheidsmomenten in het algemeen calculus, de discipline van de wiskunde die dergelijke continue variabelen aankan., Aangezien het traagheidsmoment van een puntmassa wordt gedefinieerd door
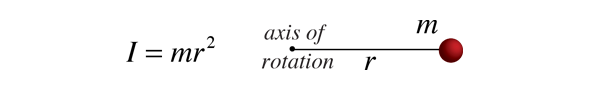
, heeft het traagheidsmoment van een oneindig massa-element dm dezelfde vorm. Dit soort massa-element wordt een differentieel element van massa genoemd en het traagheidsmoment wordt gegeven door

merk op dat het differentieel element van Traagheidsmoment dI altijd moet worden gedefinieerd met betrekking tot een specifieke rotatieas., De som over al deze massa-elementen wordt een integraal over de massa genoemd.
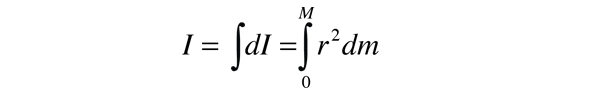
gewoonlijk wordt het massa-element dm uitgedrukt in termen van de geometrie van het object, zodat de integratie kan worden uitgevoerd over het object als geheel (bijvoorbeeld over een lange uniforme staaf).
nadat dit een algemene vorm is genoemd, is het waarschijnlijk aangewezen erop te wijzen dat het een algemene vorm is die alleen voor Assen is die “hoofdassen” kunnen worden genoemd, een term die alle assen van symmetrie van objecten omvat., Het begrip Traagheidsmoment voor algemene objecten over willekeurige Assen is een veel ingewikkelder onderwerp. Het traagheidsmoment neemt in dergelijke gevallen de vorm aan van een wiskundige tensorgrootheid die negen componenten nodig heeft om het volledig te definiëren.
| voorbeelden van integratie om Traagheidsmoment te krijgen. | rechte staaf |
| cilinder | Bol |