Bayes ‘ stelling vindt veel toepassingen in de kansrekening en statistiek. Er is een kleine kans dat je nog nooit van deze stelling gehoord hebt in je leven. Blijkt dat deze stelling zijn weg heeft gevonden in de wereld van machine learning, om een van de hoog gedecoreerde algoritmen te vormen. In dit artikel leren we alles over het naïeve Bayes-algoritme, samen met de variaties voor verschillende doeleinden in machine learning.
zoals je misschien al geraden hebt, vereist dit dat we dingen vanuit een probabilistisch oogpunt bekijken., Net als bij machine learning hebben we attributen, responsvariabelen en voorspellingen of classificaties. Met behulp van dit algoritme zullen we omgaan met de kansverdelingen van de variabelen in de dataset en de waarschijnlijkheid voorspellen van de responsvariabele die tot een bepaalde waarde behoort, gegeven de attributen van een nieuwe instantie. Laten we beginnen met het herzien van de stelling van Bayes.
Bayes’ stelling
Hiermee kunnen we de waarschijnlijkheid van een gebeurtenis onderzoeken op basis van de voorkennis van een gebeurtenis die betrekking had op de eerste gebeurtenis., Dus bijvoorbeeld, de kans dat de prijs van een huis is hoog, kan beter worden beoordeeld als we weten de faciliteiten eromheen, in vergelijking met de beoordeling gemaakt zonder de kennis van de locatie van het huis. De stelling van Bayes doet precies dat.

bovenstaande vergelijking geeft de basisrepresentatie van de stelling van Bayes., Hier zijn A en B twee gebeurtenissen en,
P(A|B) : de voorwaardelijke kans dat Gebeurtenis A optreedt , gegeven dat B heeft plaatsgevonden. Dit is ook bekend als de posterior probability.
P (A) en P (B): waarschijnlijkheid van A en B zonder rekening te houden met elkaar.
P (B / A): de voorwaardelijke kans dat Gebeurtenis B optreedt , gegeven dat A heeft plaatsgevonden.
nu, laten we eens kijken hoe dit goed past bij het doel van machine learning.,
neem een eenvoudig machine learning probleem, waarbij we ons model moeten leren van een gegeven set attributen (in trainingsvoorbeelden) en dan een hypothese of een relatie met een respons variabele vormen. Dan gebruiken we deze relatie om een reactie te voorspellen, gegeven attributen van een nieuwe instantie. Met behulp van de stelling van Bayes is het mogelijk om een leerling te bouwen die de waarschijnlijkheid voorspelt van de responsvariabele die tot een bepaalde klasse behoort, gegeven een nieuwe reeks attributen.
overweeg de vorige vergelijking opnieuw. Neem nu aan dat A de responsvariabele is en B het invoerattribuut is., Dus volgens de vergelijking hebben we
P ( A / B): conditional probability of response variable behorend tot een bepaalde waarde, gegeven de input attributen. Dit is ook bekend als de posterior probability.
P (A): de eerdere waarschijnlijkheid van de responsvariabele.
P (B): de waarschijnlijkheid van opleidingsgegevens of het bewijs.
P (B / A): Dit wordt de waarschijnlijkheid van de trainingsgegevens genoemd.,
Daarom, de bovenstaande vergelijking kan worden herschreven als
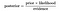
Laten we eens een probleem is, waar het aantal kenmerken is gelijk aan n en de reactie is een boolean-waarde, dus het kan in één van de twee klassen. Ook zijn de attributen categorisch (2 categorieën voor ons geval). Nu, om de classifier te trainen, moeten we P(B|A) berekenen, voor alle waarden in de instantie en reactie ruimte., Dit betekent dat we 2*(2^n -1), parameters moeten berekenen om dit model te leren. Dit is duidelijk onrealistisch in de meeste praktische leerdomeinen. Als er bijvoorbeeld 30 Booleaanse attributen zijn, dan moeten we meer dan 3 miljard parameters schatten.
naïef Bayes algoritme
de complexiteit van de bovenstaande Bayesiaanse classifier moet worden verminderd, wil het praktisch zijn. De naïeve Bayes algoritme doet dat door het maken van een aanname van voorwaardelijke onafhankelijkheid over de training dataset. Dit reduceert de complexiteit van bovengenoemd probleem drastisch tot slechts 2n.,
de aanname van voorwaardelijke onafhankelijkheid stelt dat, gegeven willekeurige variabelen X, Y en Z, we zeggen dat X voorwaardelijk onafhankelijk is van Y gegeven Z, als en alleen als de kansverdeling die X beheerst onafhankelijk is van de waarde van Y gegeven Z.
met andere woorden, X en Y zijn voorwaardelijk onafhankelijk gegeven Z dan en alleen als, gegeven de kennis dat Z voorkomt, kennis of X optreedt geen informatie geeft over de waarschijnlijkheid dat Y optreedt, en kennis of Y optreedt geen informatie geeft over de waarschijnlijkheid dat X optreedt.,
deze aanname maakt het Bayes-algoritme naïef.
gegeven, N verschillende attribuutwaarden, kan de waarschijnlijkheid nu worden geschreven als
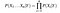
hier representeert x de attributen of kenmerken, en Y is de responsvariabele. Nu wordt P (X|Y) gelijk aan de producten van, kansverdeling van elk attribuut x gegeven Y.,
maximaliseren a Posteriori
waar we in geïnteresseerd zijn, is het vinden van de posterior probability of P(Y|X). Nu, voor meerdere waarden van Y, moeten we deze uitdrukking voor elk van hen berekenen.
gegeven een nieuwe instantie Xnew, moeten we de waarschijnlijkheid berekenen dat Y een bepaalde waarde zal aannemen, gegeven de waargenomen attribuutwaarden van Xnew en gegeven de distributies P(Y) en P(X|Y) geschat op basis van de trainingsgegevens.
dus, hoe zullen we de klasse van de respons variabele voorspellen, gebaseerd op de verschillende waarden die we bereiken voor P(Y|X)., We nemen gewoon de meest waarschijnlijke of maximale van deze waarden. Daarom is deze procedure ook bekend als het maximaliseren a posteriori.
maximaliserende waarschijnlijkheid
als we aannemen dat de responsvariabele gelijkmatig verdeeld is, dat wil zeggen dat het even waarschijnlijk is om een reactie te krijgen, dan kunnen we het algoritme verder vereenvoudigen. Met deze aanname wordt de priori of P(Y) een constante waarde, die 1/categorieën van de respons is.
aangezien de priori en het bewijs nu onafhankelijk zijn van de responsvariabele, kunnen deze uit de vergelijking worden verwijderd., Daarom wordt het maximaliseren van de posteriori gereduceerd tot het maximaliseren van de waarschijnlijkheid probleem.
Feature Distribution
zoals hierboven te zien is, moeten we de verdeling van de responsvariabele van de trainingsset schatten of een uniforme verdeling aannemen. Evenzo, om de parameters voor de distributie van een functie te schatten, moet men uitgaan van een distributie of het genereren van niet-parametrische modellen voor de functies van de training set. Dergelijke veronderstellingen staan bekend als gebeurtenismodellen. De variaties in deze veronderstellingen genereert verschillende algoritmen voor verschillende doeleinden., Voor continue distributies is de Gaussiaanse naïeve Bayes het algoritme van keuze. Voor discrete functies, multinomial en Bernoulli distributies als populair. Gedetailleerde bespreking van deze variaties valt buiten het toepassingsgebied van dit artikel.
naïeve Bayes classifiers werken echt goed in complexe situaties, ondanks de vereenvoudigde veronderstellingen en naïviteit. Het voordeel van deze classificeerders is dat ze een klein aantal trainingsgegevens nodig hebben voor het schatten van de parameters die nodig zijn voor de classificatie. Dit is het algoritme van keuze voor tekst categorisatie., Dit is het basisidee achter naïeve Bayes classifiers, dat je moet beginnen te experimenteren met het algoritme.