het Vinden van de kwadratische functies voor gegeven parabolen – Kwadratische Functies

het Vinden van de Kwadratische Functies voor Gegeven Parabolen

Er zijn zo vele verschillende types van problemen kunt u worden gevraagd met betrekking tot kwadratische vergelijkingen. In dit artikel zal de focus worden gelegd op hoe we een kwadratische vergelijking kunnen ontwikkelen uit een kwadratische grafiek met behulp van een paar verschillende methoden., Maar voordat we in dit soort problemen komen, neem even de tijd om te spelen met kwadratische uitdrukkingen op deze prachtige online grafische rekenmachine hier. Hoe comfortabeler je bent met kwadratische grafieken en uitdrukkingen, hoe makkelijker dit onderwerp zal zijn!

laten we nu ingaan op het oplossen van problemen met deze kennis, namelijk, hoe de vergelijking van een parabool te vinden!

hoe een kwadratische vergelijking uit een grafiek te vinden:

om een kwadratische vergelijking uit een grafiek te vinden, zijn er twee eenvoudige methoden die men kan gebruiken: met behulp van 2 punten, of met behulp van 3 punten.,

1) Zoek kwadratische vergelijking uit 2 punten

om een kwadratische vergelijking uit een grafiek te vinden die slechts 2 punten gebruikt, moet één van die punten de top zijn. Met de vertex en een ander punt, kunnen we deze coördinaten sub in wat wordt genoemd de “vertex vorm” en dan oplossen voor onze vergelijking., De vertex formule is als volgt, waar (d,f) is de vertex punt (x,y) is het andere punt:

(y±d)=a(x±f)2(y \pm d) = a(x \pm f)^{2}(y±d)=a(x±f)2

Vertex formulier kan ook geschreven worden in de meer “juiste” vorm, zoals:

y=a(x±f)2∓dy = a(x \pm f)^{2} \mp dy=a(x±f)2∓d

met Gebruik van deze formule, alles wat we moeten doen is de sub in de vertex en de andere punt, de oplossing voor een, en dan herschrijven van onze laatste vergelijking., De beste manier om comfortabel te worden met het gebruik van dit formulier is om een voorbeeldprobleem mee te doen.

voorbeeld:

Bepaal de vergelijking van de parabool in de afbeelding hieronder.

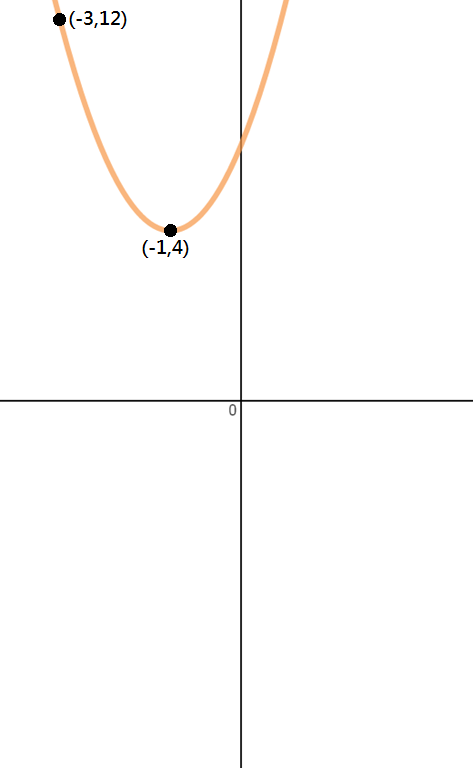
Stap 1: Identificeer punten

omdat we slechts twee punten krijgen in dit probleem, de vertex en een ander punt, we moeten Vertex formulier gebruiken om deze vraag op te lossen.,

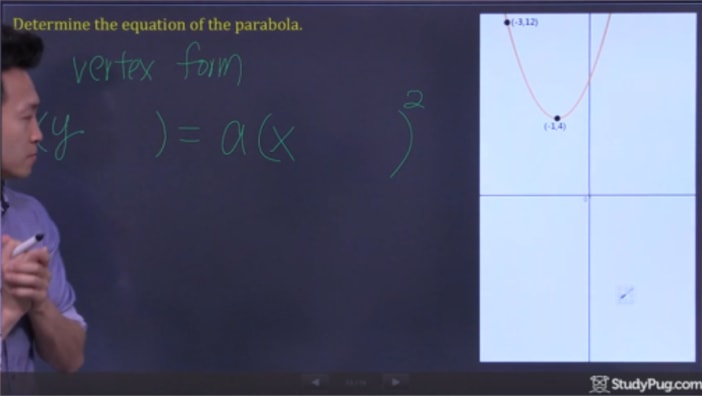
Stap 2: subpunten in de Vertex-vorm en oplossen voor “a”

nu alle we moeten doen is in onze twee punten in de vertex formule en oplossen voor “A” om alle informatie te hebben om onze uiteindelijke kwadratische vergelijking te schrijven.,4)=een(-3+1)2(12 – 4) = een(-3 + 1)^{2}(12-4)=een(-3+1)2

8=a(-2)28 = a(-2)^{2}8=a(-2)28=4a8 = 4a8=4aa=2a = 2a=2

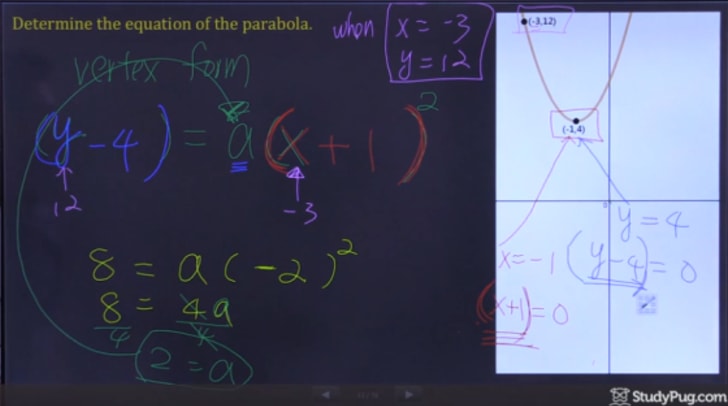
Stap 3: Schrijf Kwadratische Vergelijking

Na het oplossen van voor de “a”, nu hebben we alle informatie die we nodig hebben om te schrijven uit onze uiteindelijke antwoord op de vraag.,

y−4=2(x+1)2y – 4 = 2(x + 1)^{2}y−4=2(x+1)2

en dan, in de juiste vertex vorm van een parabool, is ons uiteindelijke antwoord:

y=2(x+1)2+4y = 2(x + 1)^{2} + 4y=2(x+1)2+4

dat maakt de les over Vertex vorm en hoe een kwadratische vergelijking te vinden van 2 punten!, Als u uw geheugen wilt vernieuwen over de gerelateerde onderwerpen zoals, hoe kwadratische uitdrukkingen in vertex-vorm op te lossen, hoe u een regelmatige kwadratische vergelijking van standaardformulier naar vertex-vorm converteert door het vierkant in te vullen, en hoe u vertex-formule gebruikt, zorg ervoor dat u onze lessen bekijkt.

2) Zoek kwadratische vergelijking uit 3 punten

in sommige gevallen, zullen we niet zo gelukkig zijn dat we het punt op de top krijgen. Als dat het geval is, kunnen we de kwadratische uitdrukking niet meer vinden met slechts twee punten, en moeten we iets anders doen., In het geval dat we informatie krijgen over de x-Onderscheppingen van een parabool, evenals een ander punt, kunnen we de kwadratische vergelijking vinden met behulp van een vergelijking die “gefactoreerde vorm”wordt genoemd. De algemene vergelijking voor de factored form formule is als volgt, waarbij b en c de x-coördinaatwaarden zijn van de x-intercepts:

y=a(x−b)(x−c)y = a(x – b)(x – c)y=a(x−b)(x−c)

Met deze formule hoeven we alleen maar deze formule te gebruiken.vervang de x-coördinaten van de x-intercepts, een ander punt, en los dan op voor A zodat we ons definitieve antwoord kunnen schrijven., Nogmaals, de beste manier om vertrouwd te raken met deze vorm van kwadratische vergelijkingen is om een voorbeeldprobleem te doen.

voorbeeld:

Bepaal de vergelijking van de parabool in de afbeelding hieronder:

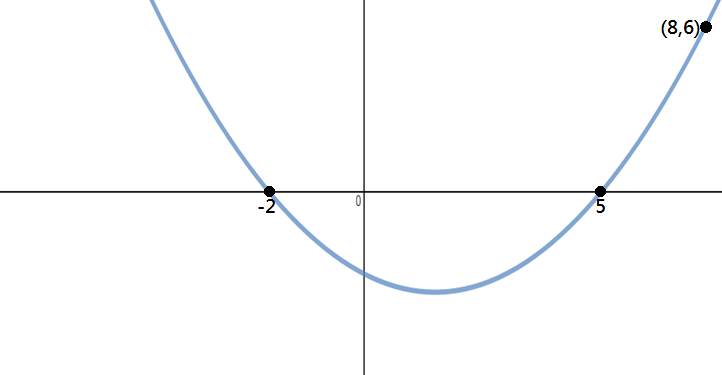
stap 1: Identificeer punten

aangezien we drie punten krijgen in dit probleem, de x-Intercept en een ander punt, kunnen we factored formulier gebruiken om deze vraag op te lossen.,

uit de grafiek kunnen we zien dat de x-intercepts -2 en 5 zijn, en het punt op de parabool is (8,6).

Stap 2: subpunten in Vertex-vorm en oplossen voor “a”

nu hoeven we alleen maar onze waarden in de factored form-formule in te vullen en oplossen voor “a” om alle informatie te hebben om onze uiteindelijke kwadratische vergelijking te schrijven.,(x – 5)y=(x+2)(x−5)

Naast, kunnen we gebruik maken van het punt op de parabool (8,6) op te lossen voor de “a”:

6=a(8+2)(8-5)6 = een(8 + 2)(8 – 5)6=a(8+2)(8-5)6=a(10)(3)6 = a(10)(3)6=a(10)(3)6=30a6 = 30a6=30aa=15a = \frac{1}{5}a=51

Stap 3: Schrijf Kwadratische Vergelijking

Na het oplossen van voor de “a”, nu hebben we alle informatie die we nodig hebben om te schrijven uit onze uiteindelijke antwoord op de vraag.,

y = 15(x+2) (x−5)y = \frac{1}{5} (x + 2) (x – 5)y=51(x+2) (x−5)

en dat is alles! Dat zijn de twee belangrijkste methoden voor het vinden van een kwadratische functie van een gegeven parabool. Voor verdere studie naar kwadratische functies en hun grafieken, bekijk deze nuttige video ‘ s omgaan met de discriminant, grafisch kwadratische ongelijkheden, en kegelsneden.