driedimensionale vormen: veelvlakken, gebogen vaste stoffen en oppervlakte

deze pagina onderzoekt de eigenschappen van driedimensionale of “vaste” vormen.

Een tweedimensionale vorm heeft lengte en breedte. Een driedimensionale vaste vorm heeft ook diepte. Driedimensionale vormen, door hun aard, hebben een binnen en een buiten, gescheiden door een oppervlak. Alle fysieke dingen, dingen die je kunt aanraken, zijn driedimensionaal.,

deze pagina behandelt zowel rechtzijdige vaste stoffen die veelvlakken worden genoemd, die gebaseerd zijn op veelhoeken, als vaste stoffen met krommen, zoals bollen, cilinders en kegels.

veelvlakken

veelvlakken (of veelvlakken) zijn rechtzijdige vaste vormen. Veelvlakken zijn gebaseerd op veelhoeken, tweedimensionale vlakke vormen met rechte lijnen.

zie onze pagina Eigenschappen van polygonen voor meer informatie over het werken met polygonen.

veelvlakken zijn gedefinieerd als met:

• rechte randen.
• platte zijden genoemd gezichten.,
• hoeken, zogenaamde hoekpunten.

veelvlakken worden ook vaak gedefinieerd door het aantal randen, vlakken en hoekpunten die ze hebben, en ook door de vraag of hun vlakken allemaal dezelfde vorm en grootte hebben. Net als veelhoeken kunnen veelhoeken regelmatig zijn (gebaseerd op regelmatige veelhoeken) of onregelmatig (gebaseerd op onregelmatige veelhoeken). Veelvlakken kunnen ook concaaf of convex zijn.

een van de meest basale en bekende veelvlakken is de kubus. Een kubus is een regelmatige veelvlak, met zes vierkante zijden, 12 randen en acht hoekpunten.,

regelmatige veelvlakken (platonische vaste stoffen)

de vijf reguliere vaste stoffen zijn een speciale klasse van veelvlakken, waarvan alle zijden identiek zijn en elk zijde een regelmatige veelhoek is. De Platonische lichamen zijn:

• tetraëder met vier gelijkzijdige driehoekige zijden.
• kubus met zes vierkante zijden.
• octaëder met acht gelijkzijdige driehoek zijden.
• dodecaëder met twaalf vijfhoekige zijden.
• icosaëder met twintig gelijkzijdige driehoek zijden.,

zie het diagram hierboven voor een illustratie van elk van deze regelmatige veelvlakken.

Wat is een prisma?

een prisma is een veelvlak met twee overeenkomende uiteinden en platte zijden. Als je een prisma ergens over zijn lengte snijdt, evenwijdig aan een uiteinde, is de doorsnede hetzelfde-je zou eindigen met twee prisma ‘ s. De zijden van een prisma zijn parallelogrammen – vierzijdige vormen met twee paren zijden met gelijke lengte.

antiprisma ’s zijn vergelijkbaar met gewone prisma’ s, hun uiteinden komen overeen., De zijkanten van anti-prisma ‘ s bestaan echter uit driehoeken en niet uit parallelogrammen. Antiprisma ‘ s kunnen heel complex worden.

Wat is een piramide?

een piramide is een veelvlak met een polygoonbasis die verbonden is met een toppunt met rechte zijden.

hoewel we geneigd zijn te denken aan piramides met een vierkante basis, zoals de piramiden die de oude Egyptenaren bouwden, kunnen ze in feite elke polygoonbasis hebben, regelmatig of onregelmatig. Verder kan een piramide een apex in het directe centrum van zijn basis hebben, een Rechterpiramide, of kan de apex uit het midden hebben als het een schuine Piramide is.,

complexere veelvlakken

Er zijn veel meer soorten veelvlakken: symmetrisch en asymmetrisch, concaaf en convex.

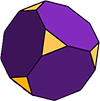
Archimedische vaste stoffen bestaan bijvoorbeeld uit ten minste twee verschillende reguliere polygonen.

de afgeknotte kubus (zoals afgebeeld) is een Archimedische vaste stof met 14 vlakken. 6 van de zijden zijn regelmatige achthoeken en de andere 8 zijn regelmatige (gelijkzijdige) driehoeken. De vorm heeft 36 randen en 24 hoekpunten (hoeken).,

driedimensionale vormen met krommen

vaste vormen met een gebogen of ronde rand zijn geen veelvlakken. Veelvlakken kunnen alleen rechte zijden hebben.

veel van de objecten om u heen zullen tenminste enkele krommen bevatten. In de meetkunde zijn de meest voorkomende gebogen vaste stoffen cilinders, kegels, bollen en tori (het meervoud voor torus).,

Common Drie-Dimensionale Vormen met Curves:
Cilinder	Kegel
Een cilinder heeft het gelijk aan de doorsnede van het ene einde tot het andere einde. Cilinders hebben twee identieke uiteinden van een cirkel of een ovaal. Hoewel vergelijkbaar, cilinders zijn niet prisma ‘ s als een prisma heeft (per definitie) parallellogram, platte zijden.,	een kegel heeft een ronde of ovale basis en een top (of top). De zijkant van de kegel loopt soepel naar de top. Een kegel is vergelijkbaar met een piramide, maar onderscheiden als een kegel heeft een enkele gebogen zijde en een cirkelvormige basis.
	Bol	Torus
bolvormige bol of bol is een geheel rond object. Elk punt op het oppervlak van een bol is een gelijke afstand tot het centrum van de bol.,	in de vorm van een ring, een band of een donut wordt een regelmatige ringtorus gevormd door een kleinere cirkel rond een grotere cirkel te draaien. Er zijn ook complexere vormen van tori.

oppervlakte

op onze pagina over het berekenen van de oppervlakte van tweedimensionale vormen wordt uitgelegd hoe u de oppervlakte van tweedimensionale vormen kunt berekenen.

Voor driedimensionale vormen hebben we het over oppervlakte, om verwarring te voorkomen.,

u kunt uw kennis over de oppervlakte van tweedimensionale vormen gebruiken om het oppervlak van een driedimensionale vorm te berekenen, aangezien elk vlak of elke zijde effectief een tweedimensionale vorm is.

u werkt daarom de oppervlakte van elk gezicht uit en voegt ze vervolgens bij elkaar.

net als bij platte vormen wordt de oppervlakte van een vaste stof uitgedrukt in vierkante eenheden: cm2, inches2, m2, enzovoort. Meer informatie over meeteenheden vindt u op onze pagina meetsystemen.,

voorbeelden van Oppervlakteberekeningen

kubus

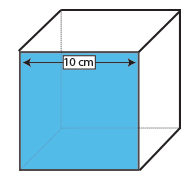
De oppervlakte van een kubus is de oppervlakte van één zijde (lengte x breedte) vermenigvuldigd met 6, omdat alle zes zijden hetzelfde zijn.

omdat het oppervlak van een kubus een vierkant is, hoeft u slechts één meting te doen – de lengte en breedte van een vierkant zijn per definitie hetzelfde.

één zijde van deze kubus is daarom 10 × 10 cm = 100cm2. Vermenigvuldig met 6, het aantal vlakken op een kubus, en we zien dat de oppervlakte van deze kubus 600cm2 is.,

andere regelmatige veelvlakken

evenzo kan de oppervlakte van de andere regelmatige veelvlakken (platonische vaste stoffen) worden berekend door de oppervlakte van één zijde te vinden en vervolgens het antwoord te vermenigvuldigen met het totale aantal zijden – zie het diagram van de Basisveelvlakken hierboven.

als de oppervlakte van een vijfhoek waaruit een dodecaëder bestaat 22cm2 is, vermenigvuldig dit dan met het totale aantal zijden (12) om het antwoord 264cm2 te geven.,

Piramide

om de oppervlakte van een standaardpiramide met vier gelijke driehoekige zijden en een vierkante basis te berekenen:

bereken eerst de oppervlakte van de basis (vierkante) lengte × breedte.

werk vervolgens de oppervlakte van één zijde (driehoek) uit. Meet de breedte langs de basis en vervolgens de hoogte van de driehoek (ook bekend als schuine lengte) van het centrale punt op de basis naar de top.,

je kunt dan ofwel je antwoord delen door 2 om je de oppervlakte van een driehoek te geven en dan vermenigvuldigen met 4 om de oppervlakte van alle vier de zijden te geven, of gewoon de oppervlakte van een driehoek vermenigvuldigen met 2.

Tel uiteindelijk de oppervlakte van de basis en de zijkanten samen om de totale oppervlakte van de piramide te vinden.

om de oppervlakte van andere typen piramiden te berekenen, tel je het oppervlak van de basis (bekend als het basisoppervlak) en het oppervlak van de zijden (laterale oppervlakte) bij elkaar op.het kan nodig zijn om de zijden afzonderlijk te meten.,

Netdiagrammen

een geometrisch net is een tweedimensionaal ‘patroon’ voor een driedimensionaal object. Netten kunnen nuttig zijn bij het uitwerken van het oppervlak van een driedimensionaal object. In het diagram hieronder kun je zien hoe de basispiramiden worden geconstrueerd, als de piramide ‘uitgevouwen’ is blijft het net over.

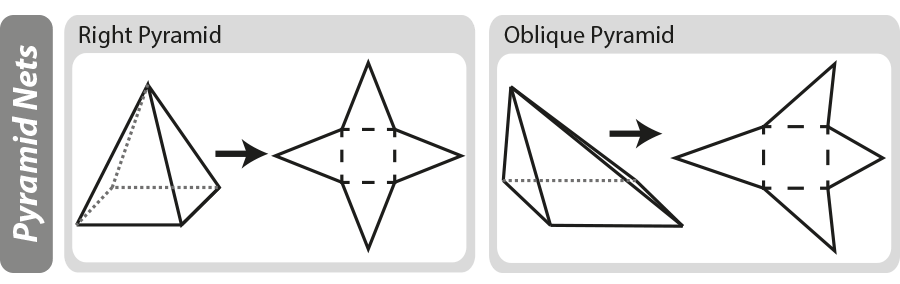
voor meer informatie over net diagrammen zie onze pagina 3D vormen en netten.

Prisma

om het oppervlak van een prisma te berekenen:

prisma ‘ s hebben twee uiteinden dezelfde en platte parallellogramzijden.,

Bereken de oppervlakte van één uiteinde en vermenigvuldig met 2.

voor een regelmatig prisma (waarbij alle zijden hetzelfde zijn) Bereken de oppervlakte van een van de zijden en vermenigvuldig met het totale aantal zijden.

voor onregelmatige prisma ‘ s (met verschillende zijden) bereken de oppervlakte van elke zijde.

voeg uw twee antwoorden samen (uiteinden × zijden) om de totale oppervlakte van het prisma te vinden.,

cilinder

om het oppervlak van een cilinder te berekenen is het nuttig na te denken over de samenstellende delen van de vorm. Stel je een blik suikermaïs voor – het heeft een boven-en een onderzijde, die beide cirkels zijn. Als je de zijkant langs de lengte snijdt en plat maakt, heb je een rechthoek. Je moet daarom de oppervlakte van twee cirkels en een rechthoek vinden.

werk eerst het oppervlak van een van de cirkels uit.

De oppervlakte van een cirkel is π (pi) × radius2.,

uitgaande van een straal van 5cm, is de oppervlakte van een van de cirkels 3,14 × 52 = 78, 5cm2.

vermenigvuldig het antwoord met 2, aangezien er twee cirkels zijn 157cm2

De oppervlakte van de zijde van de cilinder is de omtrek van de cirkel × de hoogte van de cilinder.

omtrek is gelijk aan π x 2 × straal. In ons voorbeeld, 3.14 × 2 × 5 = 31.4

meet de hoogte van de cilinder – in dit voorbeeld is de hoogte 10cm. De oppervlakte van de zijkant is 31,4 × 10 = 314cm2.,

de totale oppervlakte kan worden gevonden door de oppervlakte van de cirkels en de zijde bij elkaar op te tellen:

157 + 314 = 471cm2

Kegel

bij het berekenen van de oppervlakte van een kegel moet u de lengte gebruiken van de ‘slant’ en de straal van de basis.

Het is echter vrij eenvoudig om te berekenen:

het oppervlak van de cirkel aan de basis van de kegel is π(pi) × radius2.

In dit voorbeeld is de som 3.14 × 52 = 3.14 × 25 = 78.,5cm2

het oppervlak van de zijde, het hellende gedeelte, kan worden gevonden met behulp van deze formule:

π(pi) × straal × lengte van de schuine zijde.

in ons voorbeeld is de som 3,14 × 5 × 10 = 157cm2.

voeg ten slotte het basisoppervlak toe aan de zijkant om de totale oppervlakte van de kegel te krijgen.

78.5 + 157 = 235. 5cm2

Bol

De oppervlakte van een bol is een relatief eenvoudige uitbreiding van de formule voor het oppervlak van een cirkel.

4 × π × radius2.,

voor een bol is het vaak gemakkelijker om de diameter – de afstand over de bol te meten. U kunt dan de straal die de helft van de diameter.

De diameter van een standaard tennisbal is 2,6 inch. De radius is dus 1,3 inch. Voor de formule hebben we de straal kwadraat nodig. 1.3 × 1.3 = 1.69.

De oppervlakte van een tennisbal is daarom:

4 × 3,14 × 1,69 = 21,2264 inches2.,

Torus

om het oppervlak van een torus te berekenen, moet u twee radiuswaarden vinden.

De grote of grote straal (R) wordt gemeten vanaf het midden van het gat tot het midden van de ring.

De kleine of kleine straal (r) wordt gemeten vanaf het midden van de ring tot aan de buitenrand.

het diagram toont twee weergaven van een voorbeeld torus en hoe de radiussen (of radii) te meten.,

de berekening om de oppervlakte te vinden bestaat uit twee delen (één voor elke straal). De berekening is hetzelfde voor elk deel.

De formule is: Oppervlakte = (2nR) (2nr)

om de oppervlakte van de voorbeeldtorus uit te werken.

(2 × π × R) = (2 × 3.14 × 20) = 125.6

(2 × π × r) = (2 × 3.14 × 4) = 25.12

vermenigvuldig de twee antwoorden samen om de totale oppervlakte van de voorbeeldtorus te vinden.