
een korte uitleg en bewijs
De Rational Root Theorem (RRT) is een handig hulpmiddel om in je wiskundige arsenaal te hebben. Het biedt en snelle en vuile test voor de rationaliteit van sommige uitdrukkingen. En het helpt om rationele wortels van veeltermen te vinden.,
Hier is hoe en waarom het werkt.,e53714″>
Hoe
Stel je hebt een veelterm van graad n, geheel getal coëfficiënten:

De Rationele Root Stelling staten: Als een rationele wortel bestaat, dan zijn componenten verdelen de eerste en de laatste coëfficiënten:

De rationele wortel wordt uitgedrukt in de laagste voorwaarden., Dat betekent dat p en q geen gemeenschappelijke factoren delen. (Dat zal later belangrijk zijn.) De teller verdeelt de constante aan het einde van de veelterm; de demominator verdeelt de leidende coëfficiënt.
als voorbeeld:
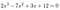
We hoeven alleen maar naar de 2 en de 12 te kijken.,:
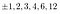
The factors of 2:
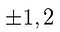
Thus, if a rational root does exist, it’s one of these:
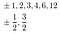
Plug each of these into the polynomial., Which one(s) — if any solve the equation? If none do, there are no rational roots.
Are any cube roots of 2 rational? A rational root, p/q must satisfy this equation.
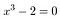
Furthermore:
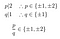
Not one of these candidates qualifies., Ga naar:
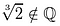
het waarom
laten we teruggaan naar onze paradigma-veelterm.,

Scoot the constant to the other side:

Now, plug in our rational root, p/q.,

Vermenigvuldig alles met de qⁿ:

Elke term aan de linkerkant heeft p gemeen. Reken daar maar op.,

het ziet er veel erger uit dan nodig is. Laten we alles tussen haakjes vervangen door een s. Het maakt ons niet uit wat erin zit.
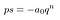
dat is veel makkelijker voor de ogen.
onthoud dat p en q gehele getallen zijn. Ze hebben ook geen gemeenschappelijke factoren., Daarom kan p qⁿ niet delen. Het moet een₀ delen:
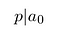
zo deelt de teller de constante term.
ga nu terug naar onze paradigma-veelterm:

Deze keer is de slechte de eerste term aan de rechterkant.,

Insert the rational root:

As before, multiply by qⁿ.

This time, the common factor on the left is q., Let’s extract it, and lump together the remaining sum as t.
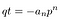
Again, q and p have no common factors. Therefore:
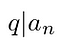
Thus proves the rational root theorem.