Calculate Log & Antilog Online

Mathematical Formulas

Calculating log (logbx):

logbx = y implies by = x.,

waarbij,

• b = basis,
• y = aantal,
• x = logwaarde.

berekenen van Antilog:

y = 10x

waarbij,

• x = aantal,
• y = antilog waarde.

logaritmen en Anti-logaritmen: hoe het werkt en zijn Betekenis

– gids geschreven door Corin B. Arenas, gepubliceerd op 1 oktober 2019

Als u zich ooit hebt afgevraagd hoe experts grote afstanden, aardbevingsintensiteit en wereldwijde economische groeipercentages bepalen, dan bent u hier aan het juiste adres.

Het berekenen van zeer grote sommen kan traag en verwarrend zijn., Maar met behulp van logaritmen (log) en antilogaritmen (antilog) kunnen berekeningen eenvoudiger worden gemaakt.

Lees verder voor meer informatie over log en antilog, hoe ze werken en waarom dit relevante wiskundige concepten zijn.

Wat is logaritme?

een logaritme is de macht waaraan een getal (ook wel de base genoemd) moet worden vermenigvuldigd om een bepaald getal te verkrijgen. Simpel gezegd Lost logaritme het probleem op:

hoe vaak vermenigvuldigen we b om een ander getal y te verkrijgen?,

logaritme telt het aantal keren dat dezelfde factor moet worden vermenigvuldigd om tot een bepaald getal te komen.

Wie heeft het bedacht?

Log werd uitgevonden in de 16e eeuw als een rekenhulpmiddel door de Schotse wiskundige, natuurkundige en astronoom John Napier. Hij schreef het boek Mirifici Logarithmorum Canonis Descriptio met tabellen en getallen die natuurlijke logaritmen bespraken, en legde de basis voor het basisconcept.

Napier bedacht de term logaritme uit het Griekse woord logos dat ‘verhouding of Verhouding’ betekent, en arithmos dat ‘getal’ betekent.,’Gecombineerd betekent het letterlijk’ ratio nummer.”

2 typen logaritmen

de natuurlijke logaritme van een getal is de logaritme van de basis van de constante e, waarbij e ongeveer gelijk is aan 2.718281828459. De vergelijking wordt geschreven als loge (x).

als een logaritme geen basis specificeert, zoals dit voorbeeld: log(1000), staat het bekend als een gemeenschappelijke logaritme die de basis 10 gebruikt.

log(1000), Het staat bekend als een gemeenschappelijke logaritme die de basis 10 gebruikt.

Hoe wordt Log gebruikt?,

zodra u begint met het berekenen van cijfers met miljoenen, miljarden en biljoenen, kan het behoorlijk belastend worden. Of het nu gaat om het tellen van veel geld, de groei van de bevolking, of het afleggen van grote afstanden, log kan voor u werken. Het kan grote sommen die lange en verwarrende vergelijkingen te betrekken vereenvoudigen, waardoor ze gemakkelijker te begrijpen.

Hier is de standaardvergelijking voor log:
logb (x) = y

waarbij

• het getal vermenigvuldigd met zichzelf (b) de basis is.
• het aantal keren dat het wordt vermenigvuldigd (y) is de logaritme.,
• het verkregen getal (x)staat tussen haakjes.

om te begrijpen hoe het concept werkt, is hier een voorbeeld met een kleiner getal:
vraag: hoeveel 2s vermenigvuldigen we om 32 te krijgen?
b= 2, x = 32

log2 (32) = y
antwoord: 2 x 2 x 2 x 2=32

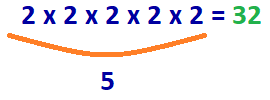
5 nummer 2s moet worden vermenigvuldigd om het nummer 32 te verkrijgen.
Het antwoord: log2(32) = 5

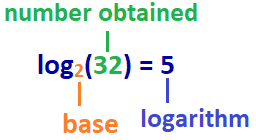
daarom is in dit voorbeeld: de logaritme van 32 met basis 2 is 5, of log basis 2 van 32 is 5.,

bovendien is log de inverse functie van exponentiatie, waarbij de wiskundige bewerking wordt geschreven als bn. b is de basis die wordt vermenigvuldigd volgens de macht van n, dat is het aantal keer dat het wordt vermenigvuldigd tot zichzelf.

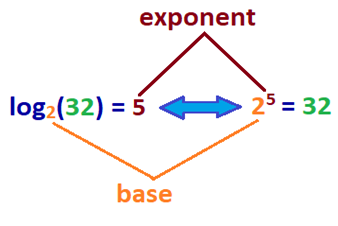
wat betekent dit? De log van een getal is de exponent waaraan basis b wordt vermenigvuldigd om een gegeven getal te verkrijgen. Om je een beter idee te geven, refereer je naar de voorbeeld log vergelijking set naast de exponentiële vergelijking hieronder.,

log	exponent
log 2(32) = 5	25 = 32

laten we Nu proberen het met een groot aantal.vraag: hoeveel 10s vermenigvuldigen we om 150.000.000.000 te krijgen?
b = 10, x = 150.000.000.000

logb(x) = y
log(150.000.000.000) = y
y = 11.1760912590557
log(150.000.000.000) = 11.,1760912590557

Dit wordt opgelost door de logfunctie in een wetenschappelijke rekenmachine te gebruiken. Of gebruik de rekenmachine op deze pagina om het antwoord te krijgen.

Hoe is Antilogarithm gerelateerd aan Log?

een lognummer kan dan worden geretourneerd naar het oorspronkelijke nummer. Dit kan worden gedaan met behulp van antilogarithm (antilog). De antilog is dus de inverse functie van log. Ook antilog functies om een vereenvoudigde log waarde exponentiate.,

om de antilog van een getal y te berekenen, moet u de logaritme basis b (meestal 10, soms de constante e) verhogen tot de macht die het getal y zal genereren.

Hier is de vergelijking voor antilog met basis 10:
10x = y
waarbij x de exponent is en y de antilog waarde.

bijvoorbeeld, als we deze vergelijking nemen, log (5) = x, zal de antilog 10x = 5 zijn.

• Log: log ( 5) = 0.698970004336019
• Antilog: 100.698970004336019 = 5

laten we het nu proberen met een groter getal.,

als we log(150.000.000.000) = x nemen, zal zijn antilog 10x = 150.000.000.000 zijn.

• Log: log10(150.000.000.000) = 11.1760912590557
• Antilog: 1011.1760912590557= 150.000.000.000

belang en toepassingen in de praktijk

vóór de uitvinding van rekenmachines werden logaritmen gebruikt om berekeningen op verschillende gebieden van kennis te vereenvoudigen, zoals navigatie, landmeetkunde, astronomie en later engineering.

stel je voor dat je in de 16e eeuw in niemandsland vaart., Navigators vertrouwden toen op de positie van sterren en een sextant mechanisme om hun exacte locatie te bepalen. Zonder moderne technologie om grote afstanden te berekenen, kunt u log gebruiken om uw berekeningen te vereenvoudigen. Nauwkeurigheid is belangrijk, of u riskeert meer dagen op zee met schamele voorraden. Minder vergelijkingen betekent minder ruimte voor fouten.

hoe zit het met andere praktische toepassingen? Levende wetenschap stelt logaritmen betrekking geometrische progressies aan rekenkundige progressies., Als je ooit repetitieve vormen en patronen in de natuur, architectuur en kunst hebt opgemerkt, bezitten deze formaties hun eigen overeenkomstige logaritmische waarden.

vandaag de dag beïnvloedt kennis van hoe deze patronen werken de manier waarop de mensheid huizen, gebouwen en stedelijke landschappen construeert en ontwerpt.

logaritmen worden ook gebruikt om de omvang en intensiteit van bepaalde schalen uit te drukken., Afgezien van grote afstanden en hoge snelheden, meet het andere zaken zoals:

• geluidsintensiteit
• geluidsfrequentie
• kracht van windstormen
• sterkte van aardbevingen
• corrosief niveau van zuren
• hardheid van mineralen
• helderheid van sterren

laten we decibels als voorbeeld nemen. Om luidsprekers 10 decibel luider te maken, moet deze worden geleverd met 10 keer het vermogen. Als je het verhoogt naar + 20 dB, zal het 100 keer het vermogen nodig hebben, en met + 30 dB zal het 1000 het vermogen nodig hebben.

bovendien verloopt de geluidsintensiteit rekenkundig., Het verandert ook proportioneel met de logaritme van een geluidsgolf die geometrisch vordert.

Hieronder is een tabel van Live Science met verschillende logaritmische schalen met hun overeenkomstige lineaire schalen.

bij het meten van snelheden en rangen

volgens Kalid Azad, de wiskundedocent achter BetterExplained.com logaritmen zijn hoe we erachter komen hoe snel iets groeit.

gemeenschappelijke logaritmen beschrijven in principe getallen in termen van hun bevoegdheden van 10. Als het gaat om rente, de logaritme is de groei van een investering.,

bij het bepalen van het BBP-groeipercentage van een land beoordelen analisten het BBP in de daaropvolgende jaren. Ze nemen het BBP van het voorgaande jaar, en het BBP van het volgende jaar, dan berekenen de logaritme om de geschatte groei te vinden.

zoekmachines gebruiken de linkgrafiek om het belang, betrouwbaarheid & autoriteit van documenten op het web te bepalen. Google ‘ s PageRank was een grote evolutie in het zoeken die de zoekrelevantie versterkt en Google search marketshare geholpen.,

volgens Azad is een landingspagina met een PageRank van 2 op een schaal van 1 tot 10 keer populairder dan een pagina met een PageRank van 1. Als een site een PageRank van 5 heeft, en een concurrent site een PageRank van 9 heeft, dan heeft het een verschil van 4 ordes van grootte.

een orde van grootte betekent ruwweg een 10x verschil, of een ranking is 1 cijfer groter in vergelijking met de andere. In dit geval is een site met een PageRank 9 100.000.000 populairder dan een site met PageRank 1.,

de Bottom Line

Log en antilog zijn belangrijke rekenmethoden die ons in staat stellen om grote sommen te vereenvoudigen. Vereenvoudiging verkort het rekenproces en maakt berekeningen gemakkelijker te begrijpen. Dit helpt de ruimte voor fouten te verminderen.

bovendien biedt het gebruik van log meetbare schalen voor het meten van natuurverschijnselen, zoals de intensiteit van aardbevingen, de kracht van windstormen en de helderheid van sterren. Op financieel gebied stellen logaritmen ons in staat de rente en de economische groei te bepalen.

Het wordt praktisch gebruikt in vele velden., Grote waarden die afhankelijk zijn van de nauwkeurigheid van de meting profiteren van het gebruik van logaritmische berekeningen.

over de auteur

Corin is een fervent onderzoeker en schrijver van financiële onderwerpen—het bestuderen van economische trends, hoe deze van invloed zijn op de bevolking, evenals hoe consumenten te helpen verstandiger financiële beslissingen te nemen. Haar andere artikelen kunnen worden gelezen op Inquirer.net en Manileno.com. ze heeft een Master ‘ s degree in Creative Writing van de University of the Philippines, een van de top academische instellingen in de wereld, en een Bachelor in Communication Arts van Miriam College.