tredimensjonale Figurer: Polyhedrons, Buet Masser og Overflate

Denne siden undersøker egenskapene til tre-dimensjonale eller «solid» former.

En to-dimensjonal form har lengde og bredde. En tre-dimensjonal solid form også har dybde. Tre-dimensjonale figurer, ved sin natur, har en innvendig og en utvendig, atskilt med en overflate. Alle fysiske gjenstander, ting du kan trykke på, er tre-dimensjonal.,

Denne siden dekker både rett-sidig faste stoffer kalt polyhedrons, som er basert på polygoner, og faste stoffer med kurver, som skåler, sylindere og kjegler.

Polyhedrons

Polyhedrons (eller polyedre) er rett-sidig solid former. Polyhedrons er basert på polygoner, to-dimensjonale fly former med rette linjer.

Se vår side på Egenskaper av Polygoner for mer om hvordan du arbeider med polygoner.

Polyhedrons er definert som det å ha:

• Rette kanter.
• Flate sider kalles ansikter.,
• Hjørner, kalt noder.

Polyhedrons er også ofte definert av antall kanter, ansikter og hjørnene de har, samt om deres ansikter er alle i samme form og størrelse. Som polygoner, polyhedrons kan være vanlig (basert på regulære polygoner) eller uregelmessig (basert på uregelmessige polygoner). Polyhedrons kan også være konkav eller konveks.

En av de mest grunnleggende og kjent polyhedrons er kuben. En kube er en vanlig polyhedron, som har seks kvadratiske flater, 12 kantene, og åtte hjørner.,

Vanlig Polyhedrons (Platonisk heldekkende objekter)

De fem vanlige faste stoffer er en spesiell klasse av polyhedrons, alle som står overfor er identisk med hvert ansikt som et regulært polygon. Den platonske faste stoffer er:

• Tetrahedrons med fire likesidet trekant ansikter.
• Kube med seks kvadratiske flater.
• Oktahedron med åtte likesidet trekant ansikter.
• dobbelt sekssidige med tolv pentagon ansikter.
• Icosahedron med tjue likesidet trekant ansikter.,

Se diagrammet ovenfor for en illustrasjon av hver av disse vanlige polyhedrons.

Hva er en Reflektor?

Et prisme er noen polyhedron som har to matchende ender og flate sider. Hvis du kutter et prisme hvor som helst langs dens lengde, parallelt til en slutt, sin cross-delen er den samme – du ville ende opp med to prismer. Sidene av et prisme er parallelograms – fire-sidig former med to par sider med lik lengde.

Antiprisms er lik vanlig prismer, deres ender kampen., Men sidene av anti-prismer er gjort opp av trekanter og ikke parallelograms. Antiprisms kan bli svært komplekse.

Hva er en Pyramide?

En pyramide er en polyhedron med et polygon base som kobles til en apex (topp-punktet) med rette sider.

Selv om vi har en tendens til å tenke på pyramidene, med et firkantet base, som de som de gamle Egypterne bygget, kan de faktisk har noen polygon base, regelmessig eller uregelmessig. Videre, en pyramide kan ha en apex i direkte sentrum av sin base, en Rett Pyramiden, eller kan ha apex utenfor sentrum når det er en Skjev Pyramide.,

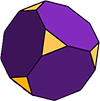
Mer Komplekse Polyhedrons

Det er mange flere typer av polyedre: symmetrisk og asymmetrisk, konkave og konvekse.

Archimedean faste stoffer, for eksempel, består av minst to forskjellige regulære polygoner.

Den avkortede cube (som vist) er en Archimedean solid med 14 ansikter. 6 av ansiktene regulær åttekant og de andre 8 er vanlig (likesidet) trekanter. Formen har 36 kanter og 24 noder (hjørner).,

tredimensjonale Figurer med Kurver

Solid figurer som inkluderer en buet eller runde kanten er ikke polyhedrons. Polyhedrons kan bare ha rette sider.

Mange av objektene rundt deg vil inkludere minst noen kurver. I geometri de vanligste buet faste stoffer er sylindre, kjegler, kuler og tori (flertall for eks).,

Vanlige Tre-Dimensjonale Figurer med Kurver:
Sylinder	Membran
En sylinder har samme tverrsnitt fra den ene enden til den andre. Sylindere har to identiske endene av enten en sirkel eller en oval. Selv om lignende, sylindere er ikke prismer som et prisme har (per definisjon) parallellogram, flate sider.,	En kjegle har en sirkulær eller oval base og en apex (eller toppunktet). Siden av membranen smalner jevnt til apeks. En membran er lik en pyramide, men tydelig som en kjegle har en enkel buet side og en rund base.
Sfære	Eks
Formet som en ball eller en globus en sfære er en helt rund gjenstand. Hvert punkt på overflaten av en kule er en lik avstand til sentrum av kula.,	Formet som en ring, et dekk eller en doughnut, en vanlig ring torus er dannet ved å dreie en mindre sirkel rundt en større sirkel. Det er også mer kompleks form av tori.

Areal

Vår side om Beregning av Området som forklarer hvordan du skal regne ut arealet av to-dimensjonale figurer og du trenger for å forstå disse grunnleggende for å beregne arealet av tre-dimensjonale figurer.

For tre-dimensjonale figurer, vi snakker om areal, for å unngå forvirring.,

Du kan bruke din kunnskap om det området av to-dimensjonale figurer for å beregne arealet av en tre-dimensjonal form, siden hvert ansikt eller siden er effektivt en to-dimensjonal form.

Du derfor regne ut arealet av hvert ansikt, og så legge dem sammen.

Som med flatskjerm former, arealet av en solid er uttrykt i square enheter: cm2, inches2, m2 og så videre. Du kan finne flere detaljer om måleenheter, på vår side-Systemer for Måling.,

Eksempler på Areal Beregninger

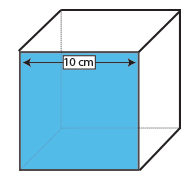
Kuben

overflaten av en terning, er det området av ett ansikt (lengde x bredde) multiplisert med 6, fordi alle seks ansikter er den samme.

Som ansiktet til en kube er et plassen du trenger bare å ta en måling – lengde og bredde av et kvadrat er per definisjon det samme.

Ett møte med denne kuben er derfor 10 × 10 cm = 100cm2. Multiplisere med 6, antall ansikter på en kube, og vi ser at arealet av denne kuben er 600cm2.,

Andre Vanlige Polyhedrons

på samme måte, arealet av andre vanlige polyhedrons (platonisk heldekkende objekter) kan regnes ut ved å finne det området av en side og deretter multiplisere svaret med det totale antall sider – se den Grunnleggende Polyhedrons diagrammet over.

Hvis området på en pentagon gjøre opp en dobbelt sekssidige er 22cm2 deretter multiplisere denne med totalt antall sider (12) å gi svar 264cm2.,

Pyramiden

for Å beregne arealet av en standard pyramide med fire like store trekantede sider og en firkantet base:

Først regne ut arealet av bunnen (square) lengde × bredde.

Neste trene området av en side (trekant). Mål bredden langs bunnen og deretter høyden av trekanten (også kjent som skrå lengde) fra det sentrale punktet på bunnen til toppen.,

deretter kan Du enten dele du svar av 2 til å gi deg arealet av en trekant og deretter multiplisere med 4 for å gi overflaten område på alle fire sidene, eller bare multiplisere arealet av en trekant med 2.

til Slutt legge til det området av undersiden og sidene sammen for å finne det totale arealet av pyramiden.

for Å beregne arealet av andre typer av pyramiden, legg sammen-området i basen (kjent som base-området) og området sider (lateral-området), du kan få behov for å måle sidene individuelt.,

Net Diagrammer

En geometrisk net er en to-dimensjonal «mønster» for et tredimensjonalt objekt. Garn kan være nyttig når du arbeider ut arealet av et tredimensjonalt objekt. I skjemaet nedenfor kan du se hvordan grunnleggende pyramidene er bygget, hvis pyramiden er «brettet ut» du sitter igjen med netto.

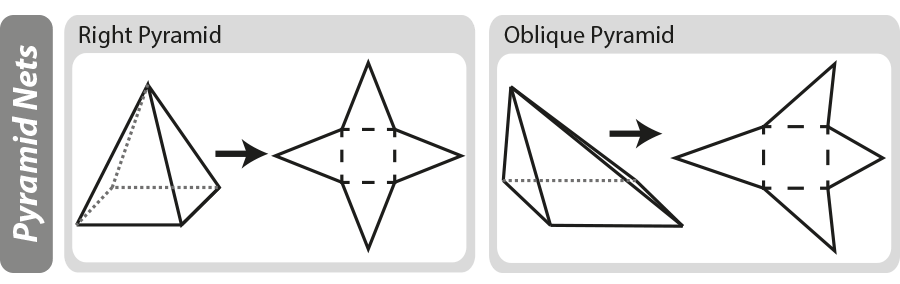
For mer informasjon om net diagrammer se vår side med 3D-Former og Garn.

Prisme

for Å beregne arealet av et prisme:

Prismer har to ender det samme og flatskjerm parallellogram sider.,

Beregn arealet av den ene enden og multiplisere med 2.

For en vanlig prisme (der alle sidene er de samme) beregn arealet av en av sidene og multiplisere med antall sider.

For uregelmessig prismer (med forskjellige sider) beregn arealet av hver side.

Legg til dine to svar sammen (ender × sider) for å finne det totale arealet av prismet.,

Sylinder

for Å beregne arealet av en sylinder det er nyttig å tenke på deler av formen. Tenk deg en boks av sweetcorn – det har en topp og en bunn, som begge er sirkler. Hvis du kutte side langs dens lengde og jevnet det du ville ha et rektangel. Du må derfor finne arealet av to sirkler og et rektangel.

Først regne ut arealet av en av sirklene.

arealet av en sirkel er π(pi) × radius2.,

Forutsatt en radius på 5 cm, området av en av sirklene er 3.14 × 52 = 78.5cm2.

Multiplisere svaret med 2, som det er to sirkler 157cm2

området på siden av sylinderen er omkretsen av sirkelen × høyden av sylinderen.

Omkretsen er lik π x 2 × radius. I vårt eksempel, 3.14 × 2 × 5 = 31.4

Måle høyden av sylinderen – for eksempel høyden er 10cm. Arealet av siden er 31.4 × 10 = 314cm2.,

Den totale overflaten området kan bli funnet ved å legge arealet av sirklene og siden sammen:

157 + 314 = 471cm2

Membran

Når du kan beregne arealet av en membran du trenger å bruke lengden på «skrå» så vel som radius av basen.

Imidlertid er det relativt enkelt å beregne:

arealet av sirkelen på undersiden av membranen, π(pi) × radius2.

I dette eksempelet summen er 3.14 × 52 = 3.14 × 25 = 78.,5cm2

området av siden, den skrå delen, kan bli funnet ved hjelp av denne formelen:

π(pi) × radius × lengde på skrå.

I vårt eksempel summen er 3.14 × 5 × 10 = 157cm2.

til Slutt legger base-området til side for å få det totale arealet av membran.

78.5 + 157 = 235.5cm2

Sfære

overflaten av en kule er en relativt enkel utvidelse av formelen for en sirkel på hotellets område.

4 × π × radius2.,

For en sfære det er ofte lettere å måle diameter – avstanden over sfære. Du kan deretter finne den radius som er halvparten av diameteren.

diameteren av en standard tennisball er 2,6 tommer. Radius er derfor 1.3 tommer. For formelen, trenger vi radius squared. 1.3 × 1.3 = 1.69.

arealet av en tennis ball er derfor:

4 × 3.14 x 1.69 = 21.2264 inches2.,

Eks

for å beregne arealet av en torus du trenger for å finne to radius verdier.

De store eller større radius (R) er målt fra midten av hullet til midten av ringen.

små eller mindre radius (r) er målt fra midten av ringen og utenfor kanten.

diagrammet viser to utsikt over et eksempel torus og hvordan å måle radiuses (eller radier).,

beregning for å finne arealet er i to deler (en for hver radius). Beregningen er de samme for hver del.

formelen er: areal = (2nR)(2nr)

for Å regne ut arealet av eksempel (eks.

(2 × π × R) = (2 × 3.14 × 20) = 125.6

(2 × π × r) = (2 × 3.14 × 4) = 25.12

Multiplisere de to svarene sammen for å finne den totale arealet av eksempel (eks.