Bayes’ teorem finner mange bruker i sannsynlighetsteori og statistikk. Det er en mikro sjanse for at du har aldri hørt om dette teoremet i ditt liv. Viser seg at dette teoremet har funnet sin vei inn i verden av maskinlæring, for å danne en av de høyt dekorert algoritmer. I denne artikkelen, vi vil lære alt om den Naive Bayes Algoritme, sammen med variasjoner for ulike formål i maskinlæring.
Som du kanskje har gjettet, dette krever oss til å se ting fra en probabilistisk synspunkt., Akkurat som i maskinlæring, vi har attributter, svar variabler og spådommer eller klassifiseringer. Ved hjelp av denne algoritmen, vi skal håndtere de sannsynlighetsfordelinger av variablene i datasettet og for å predikere sannsynligheten for at en responsvariabel som hører til en bestemt verdi, gitt de attributtene til en ny forekomst. Kan begynne med å gjennomgå Bayes’ teorem.
Bayes’ Teorem
Dette gir oss muligheten til å undersøke sannsynligheten for en hendelse basert på tidligere kunnskap om enhver hendelse som er relatert til den tidligere hendelsen., Så, for eksempel, er det stor sannsynlighet at prisen på et hus er høy, kan være bedre vurdert hvis vi vet fasiliteter rundt det, i forhold til den vurderingen som er gjort uten kjennskap til plasseringen av huset. Bayes’ teorem gjør akkurat det.

Ligningen over gir grunnleggende fremstilling av Bayes’ teorem., Her er A og B er to hendelser, og
P(A|B) : den betingede sannsynligheten for at En hendelse oppstår , gitt at B har inntruffet. Dette er også kjent som den posteriore sannsynlighet.
P(A) og P(B) : sannsynligheten for at A og B, uten hensyn til hverandre.
P(B|A) : den betingede sannsynligheten for at hendelse B oppstår , gitt at En har oppstått.
Nå, la oss se hvordan dette passer godt til formålet med maskinlæring.,
Ta en enkel maskin læring problem, hvor vi trenger å lære om vår modell fra et gitt sett av attributter(i trening eksempler), og deretter danne en hypotese eller et forhold til en responsvariabel. Så bruker vi dette forhold til å forutsi et svar, gitt attributtene til en ny forekomst. Ved hjelp av Bayes’ teorem, det er mulig å bygge en elev som anslår sannsynligheten for responsvariabel tilhørighet til noen klasse, gitt et nytt sett med attributter.
Vurdere tidligere ligning igjen. Nå, anta at A er responsvariabel og B er inngang attributtet., Så i henhold til ligning, har vi
P(A|B) : betinget sannsynlighet for respons variabel som hører til en bestemt verdi, gitt innspill attributter. Dette er også kjent som den posteriore sannsynlighet.
P(A) : Den tidligere sannsynligheten for responsvariabel.
P(B) : sannsynligheten for opplæring i data eller dokumentasjon.
P(B|A) : Dette er kjent som sannsynligheten for opplæring i data.,
Derfor, ligningen over kan bli omskrevet som
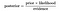
La oss ta et problem, der antall attributter er lik n, og responsen er en boolsk verdi, dvs. det kan være i en av de to klassene. Også de attributtene er kategoriske(2 kategorier for vårt tilfelle). Nå, for å trene classifier, vil vi trenger for å beregne P(B|A), for alle verdier i forekomst og reaksjon plass., Dette betyr at vi må beregne 2*(2^n -1), parametere for å lære denne modellen. Dette er helt klart urealistisk i de fleste praktiske læring domener. For eksempel, hvis det er 30 boolske attributter, så vi trenger for å beregne mer enn 3 milliarder kroner parametere.
Naive Bayes Algoritme
kompleksiteten av de ovennevnte Bayesiansk classifier må reduseres for at det skal være praktisk. Den naive Bayes algoritme gjør det ved å lage en forutsetning om betinget uavhengighet over trening dataset. Dette drastisk reduserer kompleksiteten av ovennevnte problem å bare 2n.,
Den forutsetning av betinget uavhengighet sier at, gitt tilfeldige variable X, Y og Z, vi sier at X er betinget uavhengig av Y gitt Z, hvis, og bare hvis sannsynlighetsfordeling som regulerer X er uavhengig av verdien av Y gitt Z.
med andre ord, X og Y er betinget uavhengig gitt Z hvis, og bare hvis, gitt kunnskap som Z oppstår, kunnskap om X oppstår gir ingen informasjon om sannsynligheten for Y forekommende, og kunnskap om Y oppstår gir ingen informasjon om sannsynligheten for at X er oppstått.,
Denne forutsetningen gjør Bayes algoritme, naiv.
Gitt, n forskjellige attributt verdier, sannsynligheten nå kan skrives som
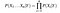
Her, X representerer egenskaper eller funksjoner, og Y er responsvariabel. Nå, P(X|Y) blir lik produkter av, sannsynlighetsfordeling av hver egenskap X gitt Y.,
Maksimering av a Posteriori
Hva vi er interessert i, er å finne den bakre sannsynligheten P(Y|X). Nå, for flere verdier av Y, vil vi trenger for å beregne dette et uttrykk for hver av dem.
Gitt en ny forekomst Xnew, vi trenger for å beregne sannsynligheten for at Y skal ta på en gitt verdi, gitt de observerte attributt verdier av Xnew og gitt fordelinger P(Y) og P(X|Y) estimert ut fra trening data.
Så, hvordan kan vi forutsi klasse av responsvariabel, basert på de ulike verdiene vi tilegner for P(Y|X)., Vi bare ta den mest sannsynlige eller maksimum av disse verdiene. Derfor er denne fremgangsmåten er også kjent som maksimerer a posteriori.
Maksimere Sannsynligheten
Hvis vi antar at responsvariabel er jevnt fordelt, er at det er like sannsynlig å få noen respons, så vi kan ytterligere forenkle algoritmen. Med denne antakelsen priori eller P(Y) blir en konstant verdi, som er 1/kategorier av svar.
Så, priori og bevis er nå uavhengig av responsen variable, disse kan bli fjernet fra ligningen., Derfor maksimere den posteriori er redusert for å maksimere sannsynligheten problem.
– Funksjonen Distribusjon
Som vi har sett ovenfor, må vi anslå fordeling av svar variabel fra trening satt til eller påtar seg uniform fordeling. På samme måte, for å estimere parametrene for en funksjon fordeling, må man anta en distribusjon eller generere nonparametric modeller for funksjoner fra trening sett. Slike forutsetninger er kjent som event-modeller. Variasjoner i disse forutsetningene genererer forskjellige algoritmer for ulike formål., For kontinuerlige fordelinger, den Gaussiske naive Bayes er algoritmen av valget. For diskrete funksjoner, multinomial og Bernoulli-distribusjoner som populære. Detaljert diskusjon av disse variasjonene er utenfor omfanget av denne artikkelen.
Naive Bayes classifiers fungerer veldig bra i komplekse situasjoner, til tross for den forenklede forutsetninger og naivitet. Fordelen med disse classifiers er at de krever lite antall av trening data for å estimere parametere som er nødvendig for klassifisering. Dette er algoritmen valg for tekst-kategorisering., Dette er den grunnleggende ideen bak naive Bayes classifiers, som du trenger for å begynne å eksperimentere med algoritmen.