
En kort forklaring og bevis
Den Rasjonelle Root-Teoremet (RRT) er et godt redskap å ha med i matematiske arsenal. Det gir en rask og skitne test for rasjonalitet av noen uttrykk. Og det hjelper å finne rasjonelle røtter av polynomer.,
Her er hvordan og hvorfor det fungerer.,e53714″>
Hvordan
Tenk deg at du har et polynom av grad n, med heltall koeffisienter:

Den Rasjonelle Root-Teoremet sier: Hvis en rasjonell roten finnes, deretter komponentene vil dele den første og siste koeffisienter:

Den rasjonelle roten er uttrykt i laveste vilkår., Det betyr at p og q dele noen felles faktorer. (Det vil være viktig senere.) Teller deler konstant på slutten av polynom; den demominator deler fører koeffisient.
Som et eksempel:
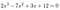
Vi trenger bare å se på 2 og 12.,:
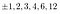
The factors of 2:
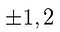
Thus, if a rational root does exist, it’s one of these:
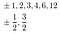
Plug each of these into the polynomial., Which one(s) — if any solve the equation? If none do, there are no rational roots.
Are any cube roots of 2 rational? A rational root, p/q must satisfy this equation.
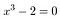
Furthermore:
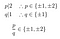
Not one of these candidates qualifies., Gå til:
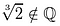
Hvorfor
La s go back (gå tilbake til våre paradigme polynom.,

Scoot the constant to the other side:

Now, plug in our rational root, p/q.,

Multiplisere alt av qⁿ:

Hver termin på venstre side har p felles. Faktor det ut.,

Det ser mye verre ut enn det trenger å være. La oss erstatte alle at ting i parentes med en s. Vi vet egentlig ikke bryr seg hva som er i det.
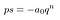
Det er mye enklere på øynene.
Husk at p og q er heltall. De deler også noen felles faktorer., Derfor, p kan ikke dele qⁿ. Det må dele a₀:
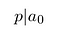
Derfor, teller deler konstant sikt.
Nå, gå tilbake til vårt paradigme polynom:

Denne gangen, det ille det første uttrykket på høyre side.,

Insert the rational root:

As before, multiply by qⁿ.

This time, the common factor on the left is q., Let’s extract it, and lump together the remaining sum as t.
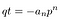
Again, q and p have no common factors. Therefore:
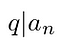
Thus proves the rational root theorem.