1913 Bohr-modellen av hydrogen atom ble erstattet av Schrodingerʹs bølge mekanisk modell i 1926. Imidlertid, Bohrʹs modellen er fortsatt lønnsomt lært i dag på grunn av sine konseptuelle og matematiske enkelhet, og fordi det innført en rekke viktige kvantemekaniske ideer, som quantum tall, kvantisering av observerbare egenskaper, quantum hoppe og stasjonær tilstand.,
Bohr beregnet manifold av tillatt elektron energi ved å balansere den mekaniske krefter (sentripetale og elektron‐kjernen) på et elektron du utfører en sirkulær bane med radius R om kjernen, og deretter arbitarily quantizing sin drivmoment. Endelig av fiat han erklærte at elektron var i en ikke‐stråler stasjonær tilstand fordi en bane (akselerasjon) kostnad utstråler energi og vil kollapse i motsatt ladning kjernen.,
I 1924 de Broglie framlegg om bølge‐partikkel dualitet for elektronet og andre massive partikler, og dermed gi mulighet til å fjerne noen av arbitariness fra Bohrʹs modell. For eksempel, et elektron med wave egenskaper er underlagt konstruktiv og destruktiv interferens. Som det vil bli vist dette fører naturligvis til kvantisering av elektron momentum og kinetisk energi, og dermed en manifold av tillatt energi stater for elektronet i forhold til kjernen., De Broglie‐Bohr-modellen av hydrogen atom presentert her behandler elektronet som en partikkel på en ring med bølge‐lignende egenskaper.
\
de Broglie-hypotesen er at saken har bølge-lignende egenskaper.
\
konsekvensen av de Broglieʹs hypotese; en integrert antall bølgelengder må passe innenfor omkretsen av bane. Dette introduserer quantum tall som kan ha verdier 1,2,3,… N = 4 electron staten er vist nedenfor.,
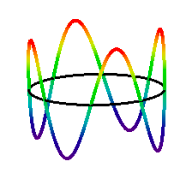
\
Substitusjon av den første ligningen til den andre ligningen viser at fart er quantized.
\
Hvis momentum er quantized, så er kinetisk energi.
\
Som betyr at den totale energien er quantized. Det andre begrepet er elektron‐proton elektrostatisk potensiell energi.
Den kvantemekaniske tolkning av disse ʺBohr orbitsʺ er at de er stasjonære tilstander. På tross av det faktum at vi bruker uttrykket for kinetisk energi, noe som innebærer electron bevegelse, er det ingen bevegelse., Elektronet opptar bane som en partikkel‐bølge, det er ikke i bane rundt kjernen. Hvis det var i bane rundt i en klassisk forstand at det ville stråle ut energi og raskt kollapse inn i kjernen. Klart stabilitet i saken krever kvantemekaniske versjon av kinetisk energi.
bakken staten energi og bane radius av elektronet i hydrogenatomet er funnet ved å plotte den energi som en funksjon av orbital radius. Bakken staten er den minste i det totale energi-kurven., Naturlig kalkulus kan brukes til å få den samme informasjonen ved å minimere energi med hensyn til bane radius. Imidlertid, den grafiske metoden har kraft til å belyse spørsmålet om atomic stabilitet.
Fundamentale konstanter: elektron kostnad, elektron masse, plancks konstant, vakuum permitivity.
Quantum tall og konvertering faktum mellom meter og picometers og joule og attojoules.
\
\
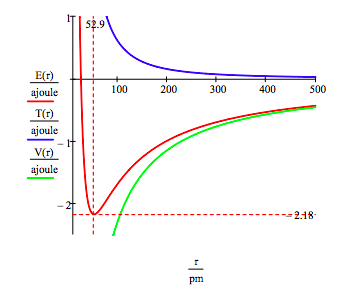
Denne figuren viser at atomic stabilitet innebærer en balanse mellom potensiell og kinetisk energi., Elektronet er trukket mot kjernen av attraktive potensiell energi samhandling (~ -1/R), men er forhindret fra å kollapse inn i kjernen av ekstremt stor kinetisk energi (~1/R2) forbundet med små baner.
Som vist nedenfor, grafisk tilnærming kan også brukes til å finne den elektroniske spent stater.
\
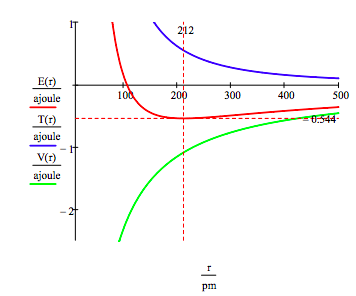
Som nevnt tidligere mangfoldet av tillatt electron energier kan også fås ved å minimere energi med hensyn til bane radius. Denne prosedyren gir,