Forholdet mellom Trykk og Volum: Boyles Lov
Som trykket på en gass øker, øker volumet på gassen reduseres fordi gassen partikler er tvunget tettere sammen. I motsatt fall, som trykket på en gass reduseres, gass volumet øker, fordi gass partikler kan nå flytte lenger fra hverandre., Vær ballonger få større som de stige gjennom atmosfæren til områder med lavere trykk, fordi volumet av gass har økt, det vil si at den atmosfæriske gass utøver mindre press på overflaten av ballongen, slik at interiøret gass som utvider seg til interne og eksterne presset er like.
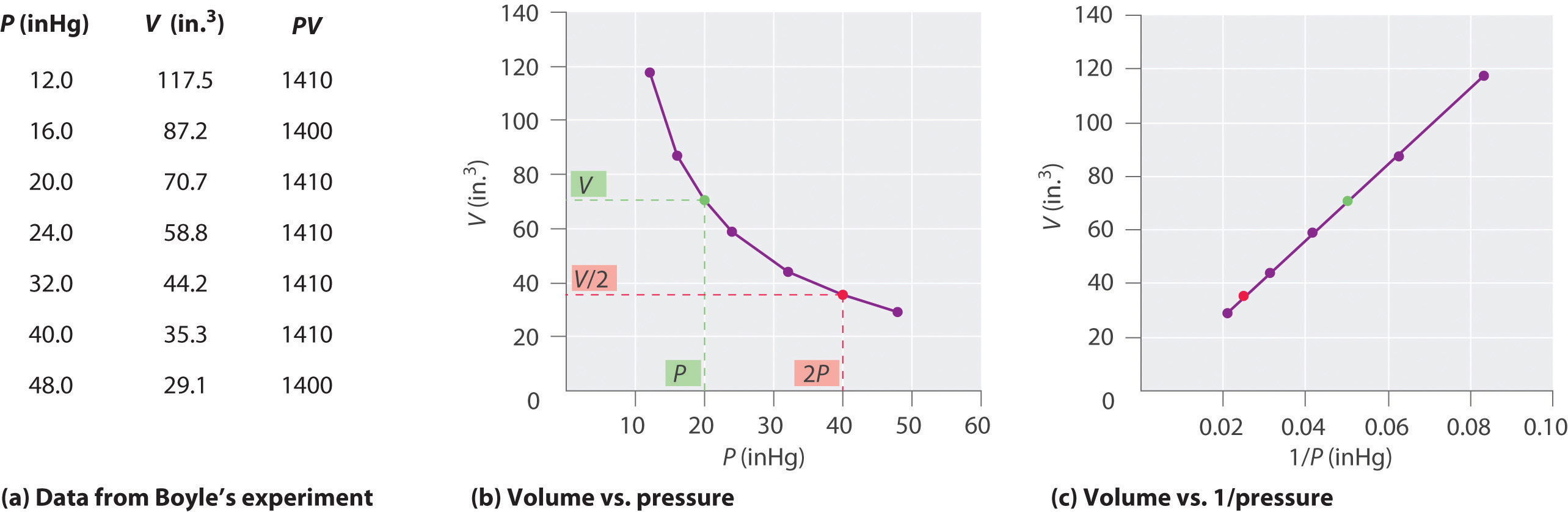
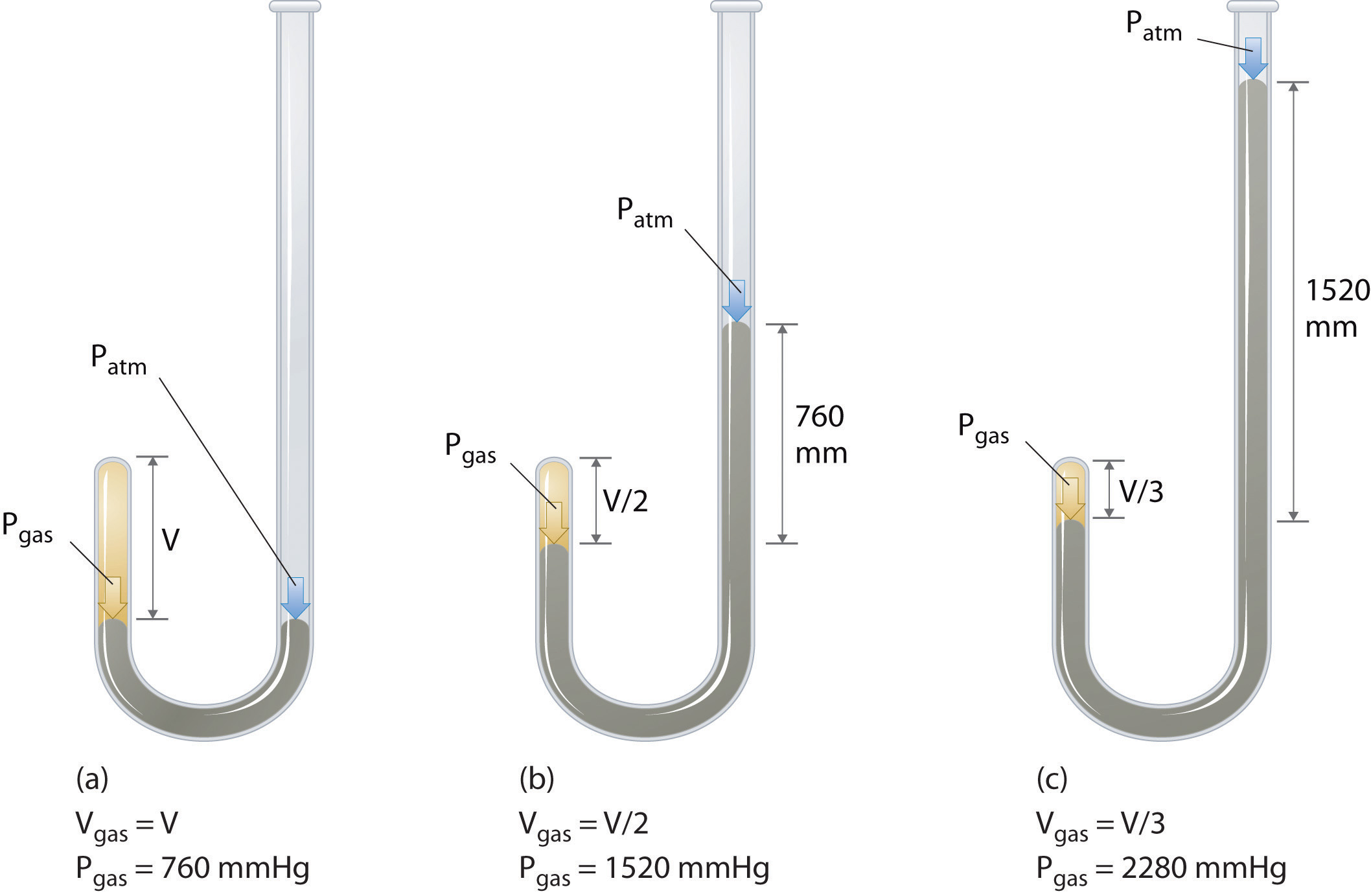
Den Irske kjemikeren Robert Boyle (1627-1691) gjennomført noen av de tidligste forsøkene som bestemte kvantitative forholdet mellom trykket og volumet av en gass. Boyle brukte en J-formet rør delvis fylt med kvikksølv, som vist i Figur \(\PageIndex{1}\)., I disse eksperimentene, en liten mengde av en gass eller luft er fanget ovenfor mercury-kolonnen, og volumet er målt ved atmosfærisk trykk og konstant temperatur. Mer kvikksølv helles deretter i åpne-arm for å øke trykket på gassen for eksempel. Trykket på gassen er det atmosfæriske trykket pluss forskjellen i høyder av kvikksølv kolonner, og den resulterende volum måles. Denne prosessen gjentas til det ikke er mer plass i åpen arm eller volumet av gassen som er for små til å bli målt nøyaktig., Data slik som de som er fra en av Boyle ‘ s egne eksperimenter kan plottes på flere måter (Figur \(\PageIndex{2}\)). En enkel tomt på \(V\) versus \(S\) gir en kurve kalles en hyperbel og avslører en invers sammenheng mellom trykk og volum: når trykket blir doblet volumet reduseres med en faktor på to. Dette forholdet mellom de to mengder er beskrevet som følger:
\
å Dividere begge sider av \(S\) gir en ligning som illustrerer det omvendte forholdet mellom \(S\) og \(V\):
\
eller
\
hvor ∝ symbolet er lese «er proporsjonal.»En tomt på V versus 1/S er dermed en rett linje hvis skråningen er lik konstant i Ligningen 6.2.1 og Ligning 6.2.3. Å dividere begge sider av Ligningen 6.2.1 av V i stedet for P gir en lignende sammenheng mellom P og 1/V., Den numeriske verdien av den konstante avhenger av mengden av gass som brukes i eksperimentet, og på den temperaturen som eksperimenter som er utført. Dette forholdet mellom trykk og volum er kjent som Boyles lov, etter sin oppdager, og kan være oppgitt som følger: Ved konstant temperatur, volumet av et fast beløp av en gass er omvendt proporsjonal med dens press.