å Finne den kvadratiske funksjoner for gitt parabolas – Kvadratiske Funksjoner

Finn den Kvadratiske Funksjoner for Gitt Parabolas

Det er så mange forskjellige typer av problemer du kan bli bedt om med hensyn til kvadratiske ligninger. I denne artikkelen vil hovedvekten bli lagt på hvordan vi kan utvikle en kvadratisk likning fra en kvadratisk grafen ved hjelp av et par ulike metoder., Men, før vi kommer til disse typer problemer, ta et øyeblikk å spille rundt med kvadratiske uttrykk på denne fantastiske online kalkulatoren her. Jo mer komfortabel du er med kvadratisk grafer og uttrykk, enklere dette emnet vil være!

la oss Nå komme til å løse problemer med denne kunnskapen, nemlig, hvordan å finne ligningen for en parabel!

Hvordan å Finne en Kvadratisk Likning fra en Graf:

for å finne en kvadratisk likning fra en graf, er det to enkle metoder man kan ta i bruk: ved bruk av 2 poeng, eller ved hjelp av 3 poeng.,

1) Finn Kvadratiske Ligningen fra 2 Poeng

for å finne en kvadratisk likning fra en graf ved hjelp av bare 2 poeng, ett av disse punktene må være toppunktet. Med toppunkt og ett annet punkt, kan vi sub disse koordinatene inn i det som er kalt «vertex form» og deretter løse for våre ligningen., Toppunktet formelen er som følger, der (d,f) er toppunktet punkt og (x,y) er det andre punktet:

(y±d)=a(x±f)2(y \pm d) = a(x \pm f)^{2}(y±d)=a(x±f)2

Vertex skjemaet kan også skrives i sin mer «riktig» form, slik:

y=a(x±f)2∓dy = a(x \pm f)^{2} \mp dy=a(x±f)2∓d

ved Hjelp av denne formelen, er alt vi trenger å gjøre er sub i toppunktet og andre punktet, løse for en, og deretter skrive de siste ligning., Den beste måten å bli komfortabel med å bruke dette skjemaet er å gjøre et eksempel problem med det.

Eksempel:

Finne ut ligningen til parabelen som vist på bildet nedenfor.

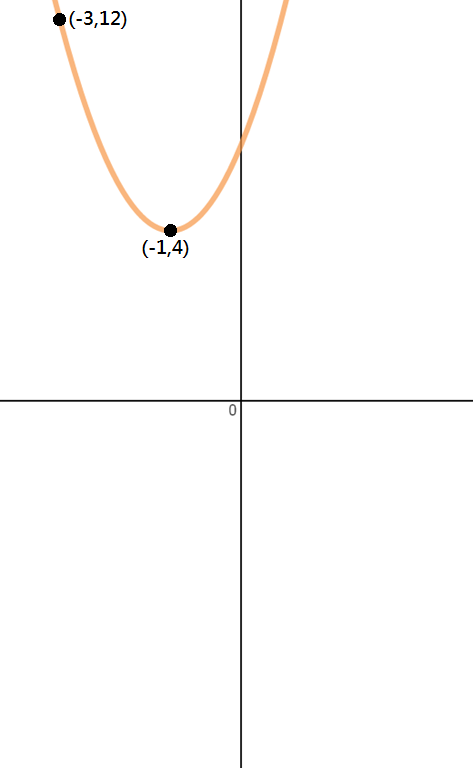
Trinn 1: Identifisere Poeng

Siden vi er bare gitt to poeng i dette problemet, vertex og et annet punkt, vi må bruke vertex skjemaet for å løse dette spørsmålet.,

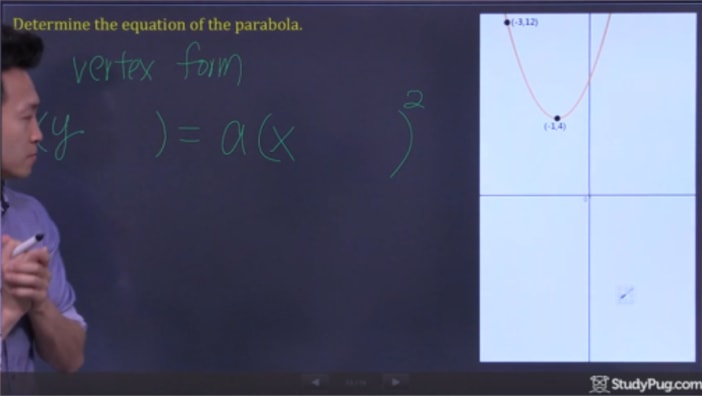
Trinn 2: Sub-Poeng Til Toppunktet Form og Løse for «a»

Nå er alt vi trenger å gjøre er sub i våre to poeng til toppunktet formel, og løse for «a» for å få all informasjon til å skrive vår siste kvadratiske ligningen.,4)=en(-3+1)2(12 – 4) = en(-3 + 1)^{2}(12-4)=en(-3+1)2

8=a(-2)28 = a(-2)^{2}8=a(-2)28=4a8 = 4a8=4aa=2a = 2a=2

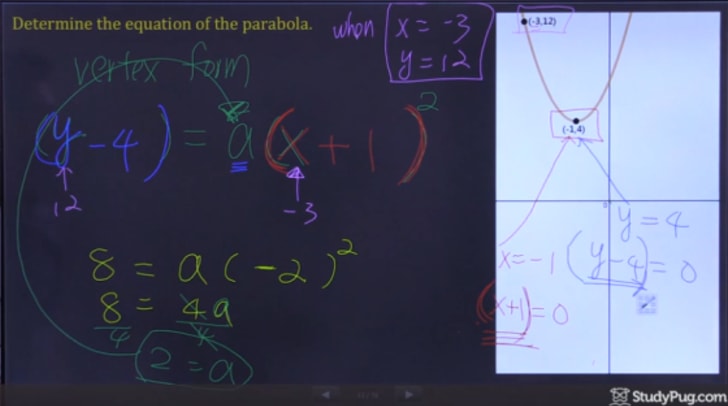
Trinn 3: Skriv Ut Kvadratiske Ligningen

Etter å løse for «a», nå har vi all informasjon vi trenger for å skrive ut vårt endelige svar.,

y−4=2(x+1)2y – 4 = 2(x + 1)^{2}y−4=2(x+1)2

Og deretter, i riktig vertex form av en parabel, vårt endelige svar er:

y=2(x+1)2+4y = 2(x + 1)^{2} + 4y=2(x+1)2+4

Som fullfører leksjon på toppunktet form og hvordan å finne en kvadratisk likning fra 2 poeng!, Hvis du ønsker å friske opp hukommelsen på relaterte emner, for eksempel, hvordan å løse kvadratiske uttrykk i toppunktet form, hvordan å konvertere en vanlig kvadratiske ligningen fra standard skjema for å vertex form av å fullføre plassen, og hvordan du bruker vertex formel, sørg for å sjekke ut våre leksjoner.

2) Finn Kvadratiske Ligningen fra 3 Poeng

I noen tilfeller vil vi ikke være så heldig å bli gitt punkt på toppunktet. Hvis det er tilfelle, kan vi ikke lenger finne den kvadratiske uttrykk med bare to poeng, og trenger å gjøre noe litt annerledes., I tilfelle at vi er gitt informasjon om x-avskjærer av en parabel, samt ett annet punkt, kan vi finne den kvadratiske ligningen ved hjelp av en ligning som er kalt «faktorisert form». Den generelle ligningen for faktorisert form formelen er som følger med b og c blir x-koordinat verdier av x-avskjærer:

y=a(x−b)(x−c)y = a(x – b)(x – c)y=a(x−b)(x−c)

ved Hjelp av denne formelen, er alt vi trenger å gjøre er sub i x-koordinatene til x-avskjærer, annet punkt, og deretter løse for en, slik at vi kan skrive ut vårt endelige svar., Igjen, den beste måten å bli komfortabel med denne formen for kvadratiske ligninger er å gjøre et eksempel på problemet.

Eksempel:

Finne ut ligningen til parabelen som vist på bildet nedenfor:

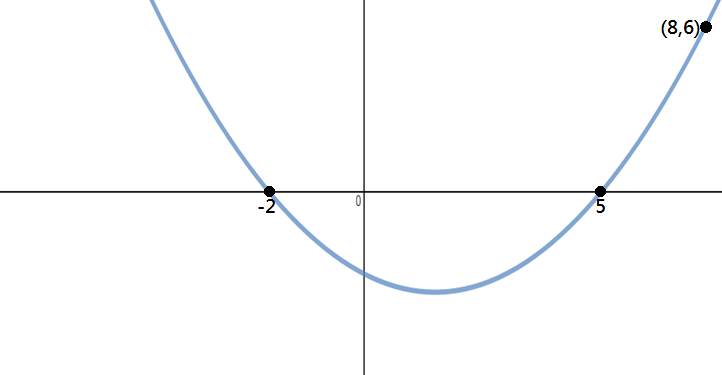
Trinn 1: Identifisere Poeng

Siden vi får tre poeng i dette problemet, x-avskjærer og et annet punkt, kan vi bruke faktorisert form for å løse dette spørsmålet.,

Fra grafen kan vi se at x-avskjærer finnes -2 og 5, og punkt på parabelen er (8,6).

Trinn 2: Sub-Poeng Til Toppunktet Form og Løse for «a»

Nå er alt vi trenger å gjøre er sub i våre verdier i faktorisert form formel, og løse for «a» for å få all informasjon til å skrive vår siste kvadratiske ligningen.,(x – 5)y=(x+2)(x−5)

Neste, vi kan bruke punkt på parabelen (8,6) for å løse for «a»:

6=en(8+2)(8-5)6 = en(8 + 2)(8 – 5)6=a(8+2)(8-5)6=a(10)(3)6 = a(10)(3)6=a(10)(3)6=30a6 = 30a6=30aa=15a = \frac{1}{5}a=51

Trinn 3: Skriv Ut Kvadratiske Ligningen

Etter å løse for «a», nå har vi all informasjon vi trenger for å skrive ut vårt endelige svar.,

y=15(x+2)(x−5)y = – \frac{1}{5} (x + 2)(x – 5)y=51(x+2)(x−5)

Og det er alt det er til det! Disse er de to viktigste metodene for å finne en kvadratisk funksjon fra et gitt parabelen. For videre studier i kvadratiske funksjoner og deres grafer, sjekk ut disse nyttige videoer arbeider med diskriminerende, grafiske kvadratiske former for ulikhet, og kjeglesnitt.