Bayes‘ theorem findet viele Anwendungen in der Wahrscheinlichkeitstheorie und Statistik. Es gibt eine kleine Chance, dass Sie noch nie in Ihrem Leben von diesem Satz gehört haben. Es stellt sich heraus, dass dieser Satz seinen Weg in die Welt des maschinellen Lernens gefunden hat, um einen der hochdekorierten Algorithmen zu bilden. In diesem Artikel erfahren wir alles über den naiven Bayes-Algorithmus und seine Variationen für verschiedene Zwecke im maschinellen Lernen.
Wie Sie vielleicht erraten haben, müssen wir die Dinge aus einer probabilistischen Sicht betrachten., Genau wie beim maschinellen Lernen haben wir Attribute, Antwortvariablen und Vorhersagen oder Klassifikationen. Mit diesem Algorithmus befassen wir uns mit den Wahrscheinlichkeitsverteilungen der Variablen im Datensatz und der Vorhersage der Wahrscheinlichkeit, dass die Antwortvariable zu einem bestimmten Wert gehört, angesichts der Attribute einer neuen Instanz. Beginnen wir mit der Überprüfung des Bayes-Theorems.
Bayes ‚ Theorem
Hiermit können wir die Wahrscheinlichkeit eines Ereignisses anhand der Vorkenntnisse eines Ereignisses untersuchen, das sich auf das frühere Ereignis bezieht., So kann zum Beispiel die Wahrscheinlichkeit, dass der Preis eines Hauses hoch ist, besser beurteilt werden, wenn wir die Einrichtungen um ihn herum kennen, verglichen mit der Bewertung ohne Kenntnis der Lage des Hauses. Bayes-theorem macht genau das.

Obige Gleichung gibt die grundlegende Gleichung darstellung des Bayes-Theorems., Hier sind A und B zwei Ereignisse und
P(A|B) : die bedingte Wahrscheinlichkeit, dass Ereignis A auftritt , vorausgesetzt, dass B aufgetreten ist. Dies wird auch als posteriore Wahrscheinlichkeit bezeichnet.
P (A) und P(B): Wahrscheinlichkeit von A und B ohne Rücksicht aufeinander.
P (B|A) : die bedingte Wahrscheinlichkeit , dass Ereignis B auftritt, vorausgesetzt, dass A aufgetreten ist.
Lassen Sie uns nun sehen, wie dies gut zum Zweck des maschinellen Lernens passt.,
Nehmen Sie ein einfaches Problem des maschinellen Lernens, bei dem wir unser Modell aus einem bestimmten Satz von Attributen(in Trainingsbeispielen) lernen und dann eine Hypothese oder eine Beziehung zu einer Antwortvariablen bilden müssen. Dann verwenden wir diese Beziehung, um eine Antwort mit Attributen einer neuen Instanz vorherzusagen. Unter Verwendung des Bayes-Theorems ist es möglich, einen Lernenden zu erstellen, der die Wahrscheinlichkeit vorhersagt, dass die Antwortvariable zu einer Klasse gehört, wenn ein neuer Satz von Attributen angegeben wird.
Betrachten Sie die Vorherige Gleichung wieder. Angenommen, A ist die Antwortvariable und B ist das Eingabeattribut., Gemäß der Gleichung haben wir also
P (A|B) : bedingte Wahrscheinlichkeit einer Variablen, die zu einem bestimmten Wert gehört, angesichts der Eingabeattribute. Dies wird auch als posteriore Wahrscheinlichkeit bezeichnet.
P (A): Die vorherige Wahrscheinlichkeit der Antwortvariablen.
P (B): Die Wahrscheinlichkeit von Trainingsdaten oder die Beweise.
P (B|A) : Dies wird als Wahrscheinlichkeit der Trainingsdaten bezeichnet.,
Daher kann die obige Gleichung als
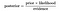
Nehmen wir ein Problem, bei dem die Anzahl der Attribute gleich n ist und die Antwort ein boolescher Wert ist, dh sie kann sich in einer der beiden Klassen befinden. Außerdem sind die Attribute kategorisch (2 Kategorien für unseren Fall). Um den Klassifikator zu trainieren, müssen wir nun P(B|A) für alle Werte im Instanz-und Antwortraum berechnen., Dies bedeutet, dass wir 2*(2^n -1) Parameter zum Erlernen dieses Modells berechnen müssen. Dies ist in den meisten praktischen Lernbereichen eindeutig unrealistisch. Wenn es beispielsweise 30 boolesche Attribute gibt, müssen wir mehr als 3 Milliarden Parameter schätzen.
Naiver Bayes-Algorithmus
Die Komplexität des obigen Bayes-Klassifikators muss reduziert werden, damit er praktisch ist. Der naive Bayes-Algorithmus macht das, indem er eine Annahme bedingter Unabhängigkeit über den Trainingsdatensatz macht. Dies reduziert die Komplexität des oben genannten Problems drastisch auf nur 2n.,
Die Annahme bedingter Unabhängigkeit besagt, dass X bei den Zufallsvariablen X, Y und Z bedingt unabhängig von Y und Z ist, wenn und nur dann, wenn die Wahrscheinlichkeitsverteilung von X unabhängig vom Wert von Y ist gegeben Z.
Mit anderen Worten, X und Y sind bedingt unabhängig von Z, wenn und nur wenn angesichts der Kenntnis, dass Z auftritt, Wissen darüber, ob X auftritt, liefert keine Informationen über die Wahrscheinlichkeit, dass Y auftritt, und Wissen darüber, ob Y auftritt, liefert keine Informationen über die Wahrscheinlichkeit, dass X auftritt.,
Diese Annahme macht den Bayes-Algorithmus naiv.
Gegeben, n verschiedene Attributwerte, die Wahrscheinlichkeit kann nun als
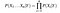
Hier stellt X die Attribute oder Merkmale dar und Y ist die Antwortvariable. Nun wird P(X|Y) gleich den Produkten von, Wahrscheinlichkeitsverteilung jedes Attributs X / Y.,
a Posteriori maximieren
Was uns interessiert, ist die posteriore Wahrscheinlichkeit oder P(Y|X) zu finden. Nun müssen wir für mehrere Werte von Y diesen Ausdruck für jeden von ihnen berechnen.
Bei einer neuen Instanz Xnew müssen wir die Wahrscheinlichkeit berechnen, dass Y einen bestimmten Wert annimmt, angesichts der beobachteten Attributwerte von Xnew und angesichts der aus den Trainingsdaten geschätzten Verteilungen P(Y) und P(X|Y).
Wie werden wir die Klasse der Antwortvariablen basierend auf den verschiedenen Werten vorhersagen, die wir für P(Y|X) erreichen?, Wir nehmen einfach das wahrscheinlichste oder Maximum dieser Werte. Daher wird dieses Verfahren auch als a posteriori Maximieren bezeichnet.
Maximierung der Wahrscheinlichkeit
Wenn wir davon ausgehen, dass die Antwortvariable gleichmäßig verteilt ist, dh es ist gleichermaßen wahrscheinlich, dass sie eine Antwort erhält, können wir den Algorithmus weiter vereinfachen. Mit dieser Annahme wird das priori oder P (Y) zu einem konstanten Wert, der 1/2 der Antwort ist.
Da priori und Evidenz nun unabhängig von der Antwortvariablen sind, können diese aus der Gleichung entfernt werden., Daher wird die Maximierung der Posteriori auf die Maximierung des Wahrscheinlichkeitsproblems reduziert.
Merkmalsverteilung
Wie oben gezeigt, müssen wir die Verteilung der Antwortvariablen aus dem Trainingssatz schätzen oder eine gleichmäßige Verteilung annehmen. Um die Parameter für die Verteilung eines Merkmals abzuschätzen, muss man in ähnlicher Weise eine Verteilung annehmen oder nichtparametrische Modelle für die Merkmale aus dem Trainingssatz generieren. Solche Annahmen werden als Ereignismodelle bezeichnet. Die Variationen in diesen Annahmen erzeugen unterschiedliche Algorithmen für verschiedene Zwecke., Für kontinuierliche Verteilungen ist der Gaußsche naive Bayes der Algorithmus der Wahl. Für diskrete Funktionen sind multinomiale und Bernoulli-Distributionen so beliebt. Detaillierte Diskussion dieser Variationen sind außerhalb des Geltungsbereichs dieses Artikels.
Naive Bayes-Klassifikatoren funktionieren in komplexen Situationen trotz der vereinfachten Annahmen und Naivität sehr gut. Der Vorteil dieser Klassifikatoren besteht darin, dass sie eine geringe Anzahl von Trainingsdaten zur Schätzung der für die Klassifizierung erforderlichen Parameter benötigen. Dies ist der Algorithmus der Wahl für die Textkategorisierung., Dies ist die Grundidee hinter naiven Bayes-Klassifikatoren, dass Sie mit dem Algorithmus experimentieren müssen.