Momento di inerzia, Forma generale
Poiché il momento di inerzia di un oggetto ordinario comporta una distribuzione continua di massa a una distanza continuamente variabile da qualsiasi asse di rotazione, il calcolo dei momenti di inerzia coinvolge generalmente il calcolo, la disciplina della matematica che può gestire tali variabili continue., Poiché il momento di inerzia di una massa puntiforme è definito da
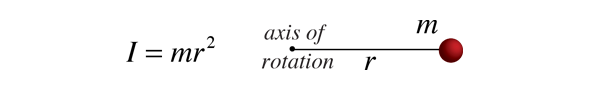
allora il momento di contributo di inerzia di un elemento di massa infinitesimale dm ha la stessa forma. Questo tipo di elemento di massa è chiamato un differenziale di massa e il suo momento di inerzia è dato da

si noti che l’elemento differenziale del momento di inerzia dI deve sempre essere definiti con riferimento ad uno specifico asse di rotazione., La somma su tutti questi elementi di massa è chiamata integrale sulla massa.
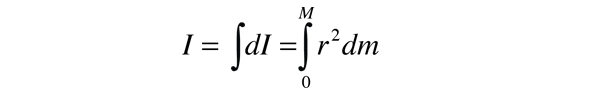
Di solito, l’elemento di massa dm sarà espresso in termini di geometria dell’oggetto, in modo che l’integrazione possa essere effettuata sull’oggetto nel suo complesso (ad esempio, su una lunga asta uniforme).
Dopo aver definito questa una forma generale, è probabilmente opportuno sottolineare che è una forma generale solo per gli assi che possono essere chiamati “assi principali”, un termine che include tutti gli assi di simmetria degli oggetti., Il concetto di momento di inerzia per oggetti generali su assi arbitrari è un argomento molto più complicato. Il momento di inerzia in questi casi assume la forma di una quantità di tensore matematico che richiede nove componenti per definirlo completamente.
| Esempi di integrazione per ottenere il momento di inerzia. | Asta diritta |
| Cilindro | |
| Sfera |