Il teorema di Bayes trova molti usi nella teoria della probabilità e nelle statistiche. C’è una micro possibilità che non hai mai sentito parlare di questo teorema nella tua vita. Si scopre che questo teorema ha trovato la sua strada nel mondo dell’apprendimento automatico, per formare uno degli algoritmi altamente decorati. In questo articolo, impareremo tutto sull’algoritmo Naive Bayes, insieme alle sue variazioni per scopi diversi nell’apprendimento automatico.
Come avrai intuito, questo ci richiede di vedere le cose da un punto di vista probabilistico., Proprio come nell’apprendimento automatico, abbiamo attributi, variabili di risposta e previsioni o classificazioni. Utilizzando questo algoritmo, ci occuperemo delle distribuzioni di probabilità delle variabili nel set di dati e prevediamo la probabilità della variabile di risposta appartenente a un particolare valore, dati gli attributi di una nuova istanza. Iniziamo rivedendo il teorema di Bayes.
Teorema di Bayes
Questo ci consente di esaminare la probabilità di un evento in base alla conoscenza preliminare di qualsiasi evento correlato all’evento precedente., Così, per esempio, la probabilità che il prezzo di una casa è alto, può essere valutato meglio se conosciamo le strutture intorno ad esso, rispetto alla valutazione fatta senza la conoscenza della posizione della casa. Il teorema di Bayes fa esattamente questo.

Equazione di cui sopra dà la rappresentazione di base del teorema di Bayes., Qui A e B sono due eventi e,
P (A / B) : la probabilità condizionale che si verifichi l’evento A , dato che B si è verificato. Questo è anche noto come probabilità posteriore.
P(A) e P(B) : probabilità di A e B senza riguardo reciproco.
P (B / A): la probabilità condizionale che si verifichi l’evento B , dato che si è verificato A.
Ora, vediamo come questo si adatta bene allo scopo dell’apprendimento automatico.,
Prendi un semplice problema di apprendimento automatico, in cui dobbiamo imparare il nostro modello da un dato insieme di attributi(negli esempi di allenamento) e quindi formare un’ipotesi o una relazione con una variabile di risposta. Quindi usiamo questa relazione per prevedere una risposta, dati gli attributi di una nuova istanza. Usando il teorema di Bayes, è possibile costruire uno studente che predice la probabilità della variabile di risposta appartenente a qualche classe, dato un nuovo set di attributi.
Considera di nuovo l’equazione precedente. Ora, supponiamo che A sia la variabile di risposta e B sia l’attributo di input., Quindi, secondo l’equazione, abbiamo
P(A|B) : probabilità condizionale di variabile di risposta appartenente a un particolare valore, dati gli attributi di input. Questo è anche noto come probabilità posteriore.
P (A): La probabilità precedente della variabile di risposta.
P (B): La probabilità di dati di allenamento o le prove.
P (B / A): Questo è noto come la probabilità dei dati di allenamento.,
Quindi, l’equazione può essere riscritta come:
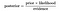
prendiamo un problema, dove il numero di attributi è uguale a n, e la risposta è un valore booleano, ovvero possono essere in una delle due classi. Inoltre, gli attributi sono categorici (2 categorie per il nostro caso). Ora, per addestrare il classificatore, dovremo calcolare P (B|A), per tutti i valori nell’istanza e nello spazio di risposta., Ciò significa che dovremo calcolare 2 * (2 ^ n -1), i parametri per imparare questo modello. Questo è chiaramente irrealistico nella maggior parte dei domini di apprendimento pratico. Ad esempio, se ci sono 30 attributi booleani, dovremo stimare più di 3 miliardi di parametri.
Algoritmo Naive Bayes
La complessità del suddetto classificatore bayesiano deve essere ridotta, perché sia pratica. L’ingenuo algoritmo di Bayes lo fa assumendo un’indipendenza condizionale sul set di dati di allenamento. Ciò riduce drasticamente la complessità del problema sopra menzionato a solo 2n.,
L’assunzione di indipendenza condizionale afferma che, dato che le variabili casuali X, Y e Z, diciamo che X è condizionalmente indipendente di Y dato Z, se e solo se la distribuzione di probabilità che disciplinano X è indipendente dal valore di Y dato Z.
In altre parole, X e Y sono condizionatamente indipendenti dato Z se e solo se, data la conoscenza che Z si verifica, la conoscenza di se X si fornisce alcuna informazione sulla probabilità di Y che si verificano, e la conoscenza di se Y si verifica non fornisce alcuna informazione sulla probabilità di X che si verificano.,
Questa ipotesi rende l’algoritmo di Bayes ingenuo.
Dato, n diversi valori di attributo, il rischio, ora, può essere scritta come:
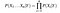
Qui, X rappresenta gli attributi o caratteristiche, e Y è la variabile di risposta. Ora, P (X|Y) diventa uguale ai prodotti di, distribuzione di probabilità di ogni attributo X dato Y.,
Massimizzare a posteriori
Quello che ci interessa è trovare la probabilità posteriore o P(Y / X). Ora, per più valori di Y, dovremo calcolare questa espressione per ciascuno di essi.
Data una nuova istanza Xnew, dobbiamo calcolare la probabilità che Y assuma un dato valore, dati i valori degli attributi osservati di Xnew e date le distribuzioni P(Y) e P(X / Y) stimate dai dati di allenamento.
Quindi, come prevederemo la classe della variabile di risposta, in base ai diversi valori che raggiungiamo per P(Y|X)., Prendiamo semplicemente il più probabile o il massimo di questi valori. Pertanto, questa procedura è anche nota come massimizzazione a posteriori.
Massimizzare la probabilità
Se assumiamo che la variabile di risposta sia distribuita uniformemente, cioè è altrettanto probabile che ottenga qualsiasi risposta, allora possiamo semplificare ulteriormente l’algoritmo. Con questa ipotesi il priori o P(Y) diventa un valore costante, che è 1/categorie della risposta.
Poiché i priori e le prove sono ora indipendenti dalla variabile di risposta, questi possono essere rimossi dall’equazione., Pertanto, la massimizzazione dei posteriori è ridotta alla massimizzazione del problema di probabilità.
Feature Distribution
Come visto sopra, dobbiamo stimare la distribuzione della variabile di risposta dal set di allenamento o assumere una distribuzione uniforme. Allo stesso modo, per stimare i parametri per la distribuzione di una caratteristica, si deve assumere una distribuzione o generare modelli non parametrici per le caratteristiche dal set di addestramento. Tali ipotesi sono note come modelli di eventi. Le variazioni di queste ipotesi genera diversi algoritmi per scopi diversi., Per le distribuzioni continue, il gaussiano naive Bayes è l’algoritmo di scelta. Per le caratteristiche discrete, distribuzioni multinomiali e Bernoulli come popolare. Discussione dettagliata di queste variazioni sono fuori dal campo di applicazione di questo articolo.
I classificatori Naive Bayes funzionano molto bene in situazioni complesse, nonostante le ipotesi semplificate e l’ingenuità. Il vantaggio di questi classificatori è che richiedono un numero limitato di dati di allenamento per stimare i parametri necessari per la classificazione. Questo è l’algoritmo di scelta per la categorizzazione del testo., Questa è l’idea di base dietro ingenui classificatori Bayes, che è necessario iniziare a sperimentare con l’algoritmo.