
Una breve spiegazione e dimostrazione
Il Teorema della radice razionale (RRT) è uno strumento utile per avere nel vostro arsenale matematico. Fornisce un test rapido e sporco per la razionalità di alcune espressioni. E aiuta a trovare radici razionali di polinomi.,
Ecco come e perché funziona.,e53714″>
Come
si Supponga di avere un polinomio di grado n, con coefficienti interi:

Il Razionale Radice Teorema dice: Se una radice razionale esiste, quindi i suoi componenti si dividono il primo e l’ultimo coefficienti:

Il razionale radice è espresso in termini più., Ciò significa che p e q non condividono fattori comuni. (Che sarà importante in seguito.) Il numeratore divide la costante alla fine del polinomio; il demominatore divide il coefficiente principale.
Come esempio:
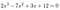
Abbiamo bisogno solo di guardare il 2 e il 12.,:
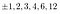
The factors of 2:
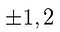
Thus, if a rational root does exist, it’s one of these:
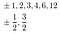
Plug each of these into the polynomial., Which one(s) — if any solve the equation? If none do, there are no rational roots.
Are any cube roots of 2 rational? A rational root, p/q must satisfy this equation.
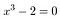
Furthermore:
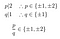
Not one of these candidates qualifies., Vai a:
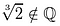
Perché
Let’s go back per il nostro paradigma polinomiale.,

Scoot the constant to the other side:

Now, plug in our rational root, p/q.,

Moltiplicare il tutto, qⁿ:

Ogni termine della sinistra ha p in comune. Fattore che fuori.,

Sembra molto peggio di quello che deve essere. Sostituiamo tutta quella roba tra parentesi con una s. Non ci interessa davvero cosa c’è dentro.
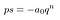
Che è molto più facile per gli occhi.
Ricorda che p e q sono numeri interi. Inoltre non condividono fattori comuni., Pertanto, p non può dividere qⁿ. Si deve dividere a₀:
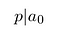
Così, il numeratore divide il termine costante.
Ora, tornare al nostro modello polinomiale:

Questa volta, il brutto, il primo termine a destra.,

Insert the rational root:

As before, multiply by qⁿ.

This time, the common factor on the left is q., Let’s extract it, and lump together the remaining sum as t.
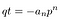
Again, q and p have no common factors. Therefore:
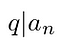
Thus proves the rational root theorem.