Forme tridimensionali: poliedri, solidi curvi e superficie

Questa pagina esamina le proprietà delle forme tridimensionali o “solide”.

Una forma bidimensionale ha lunghezza e larghezza. Una forma solida tridimensionale ha anche profondità. Le forme tridimensionali, per loro natura, hanno un interno e un esterno, separati da una superficie. Tutti gli oggetti fisici, le cose che puoi toccare, sono tridimensionali.,

Questa pagina copre sia i solidi rettilinei chiamati poliedri, che si basano su poligoni, sia i solidi con curve, come globi, cilindri e coni.

Poliedri

I poliedri (o poliedri) sono forme solide diritte. I poliedri sono basati su poligoni, forme piane bidimensionali con linee rette.

Vedi la nostra pagina Proprietà dei poligoni per ulteriori informazioni sul lavoro con i poligoni.

I poliedri sono definiti come aventi:

• Bordi diritti.
• Lati piatti chiamati facce.,
• Angoli, chiamati vertici.

I poliedri sono spesso definiti anche dal numero di bordi, facce e vertici che hanno, nonché dal fatto che le loro facce abbiano tutte la stessa forma e dimensione. Come i poligoni, i poliedri possono essere regolari (basati su poligoni regolari) o irregolari (basati su poligoni irregolari). I poliedri possono anche essere concavi o convessi.

Uno dei poliedri più basilari e familiari è il cubo. Un cubo è un poliedro regolare, con sei facce quadrate, 12 bordi e otto vertici.,

Poliedri regolari (Solidi platonici)

I cinque solidi regolari sono una classe speciale di poliedri, le cui facce sono tutte identiche e ogni faccia è un poligono regolare. I solidi platonici sono:

• Tetraedro con quattro facce triangolari equilatere.
• Cubo con sei facce quadrate.
• Ottaedro con otto facce triangolari equilatere.
• Dodecaedro con dodici facce del pentagono.
• Icosaedro con venti facce triangolari equilatere.,

Vedere il diagramma sopra per un’illustrazione di ciascuno di questi poliedri regolari.

Che cos’è un prisma?

Un prisma è qualsiasi poliedro che ha due estremità corrispondenti e lati piatti. Se tagli un prisma ovunque lungo la sua lunghezza, parallelo a un’estremità, la sua sezione trasversale è la stessa-finiresti con due prismi. I lati di un prisma sono parallelogrammi-forme a quattro lati con due coppie di lati di uguale lunghezza.

Gli antiprismi sono simili ai prismi regolari, le loro estremità corrispondono., Tuttavia i lati degli anti-prismi sono costituiti da triangoli e non da parallelogrammi. Gli antiprismi possono diventare molto complessi.

Che cos’è una piramide?

Una piramide è un poliedro con una base poligonale che si collega ad un apice (punto superiore) con lati diritti.

Anche se tendiamo a pensare a piramidi a base quadrata, come quelle che costruivano gli antichi Egizi, possono infatti avere qualsiasi base poligonale, regolare o irregolare. Inoltre, una piramide può avere un apice nel centro diretto della sua base, una Piramide destra, o può avere l’apice fuori centro quando è una piramide obliqua.,

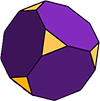
Poliedri più complessi

Esistono molti altri tipi di poliedri: simmetrici e asimmetrici, concavi e convessi.

I solidi archimedei, ad esempio, sono costituiti da almeno due diversi poligoni regolari.

Il cubo troncato (come illustrato) è un solido archimedeo con 14 facce. 6 delle facce sono ottagoni regolari e gli altri 8 sono triangoli regolari (equilateri). La forma ha 36 bordi e 24 vertici (angoli).,

Le forme tridimensionali con curve

Le forme solide che includono un bordo curvo o rotondo non sono poliedri. I poliedri possono avere solo lati diritti.

Molti degli oggetti intorno a te includeranno almeno alcune curve. In geometria i solidi curvi più comuni sono cilindri, coni, sfere e tori (il plurale per toro).,

Comuni Forme Tridimensionali con le Curve:
Cilindro	Cono
Un cilindro ha la stessa sezione da un’estremità all’altra. I cilindri hanno due estremità identiche di un cerchio o di un ovale. Anche se simili, cilindri non sono prismi come un prisma ha (per definizione) parallelogramma, lati piatti.,	Un cono ha una base circolare o ovale e un apice (o vertice). Il lato del cono si assottiglia dolcemente verso l’apice. Un cono è simile a una piramide ma distinto come un cono ha un singolo lato curvo e una base circolare.
Sfera	Toro
A forma di palla o globo una sfera è un oggetto completamente rotondo. Ogni punto sulla superficie di una sfera è una distanza uguale al centro della sfera.,	A forma di anello, pneumatico o ciambella, un toro ad anello regolare è formato ruotando un cerchio più piccolo attorno a un cerchio più grande. Ci sono anche forme più complesse di tori.

Superficie

La nostra pagina sul calcolo dell’area spiega come calcolare l’area delle forme bidimensionali e devi capire queste basi per calcolare l’area delle forme tridimensionali.

Per le forme tridimensionali, si parla di superficie, per evitare confusione.,

Puoi usare le tue conoscenze sull’area delle forme bidimensionali per calcolare l’area superficiale di una forma tridimensionale, poiché ogni faccia o lato è effettivamente una forma bidimensionale.

Quindi si elabora l’area di ogni faccia e quindi si aggiungono insieme.

Come per le forme piatte, la superficie di un solido è espressa in unità quadrate: cm2, pollici2, m2 e così via. Puoi trovare maggiori dettagli sulle unità di misura sulla nostra pagina Sistemi di misura.,

Esempi di calcolo della superficie

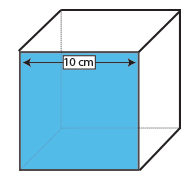
Cubo

La superficie di un cubo è l’area di una faccia (lunghezza x larghezza) moltiplicata per 6, perché tutte e sei le facce sono uguali.

Poiché la faccia di un cubo è un quadrato, devi solo prendere una misura: la lunghezza e la larghezza di un quadrato sono, per definizione, le stesse.

Una faccia di questo cubo è quindi 10 × 10 cm = 100cm2. Moltiplicare per 6, il numero di facce su un cubo, e troviamo che la superficie di questo cubo è 600cm2.,

Altri poliedri regolari

Allo stesso modo, la superficie degli altri poliedri regolari (solidi platonici) può essere elaborata trovando l’area di un lato e quindi moltiplicando la risposta per il numero totale di lati – vedere il diagramma di base dei poliedri sopra.

Se l’area di un pentagono che costituisce un dodecaedro è 22cm2, moltiplicalo per il numero totale di lati (12) per dare la risposta 264cm2.,

Piramide

Per calcolare la superficie di una piramide standard con quattro lati triangolari uguali e una base quadrata:

Prima elaborare l’area della base (quadrata) lunghezza × larghezza.

Quindi elaborare l’area di un lato (triangolo). Misurare la larghezza lungo la base e quindi l’altezza del triangolo (noto anche come lunghezza inclinata) dal punto centrale sulla base all’apice.,

Puoi quindi dividere la risposta per 2 per darti l’area superficiale di un triangolo e quindi moltiplicare per 4 per dare l’area superficiale di tutti e quattro i lati, o semplicemente moltiplicare l’area superficiale di un triangolo per 2.

Infine aggiungi l’area della base e dei lati insieme per trovare la superficie totale della piramide.

Per calcolare la superficie di altri tipi di piramide, sommare l’area della base (nota come area di base) e l’area dei lati (area laterale), potrebbe essere necessario misurare i lati individualmente.,

Diagrammi netti

Una rete geometrica è un ‘pattern’ bidimensionale per un oggetto tridimensionale. Le reti possono essere utili quando si lavora la superficie di un oggetto tridimensionale. Nel diagramma qui sotto potete vedere come piramidi di base sono costruiti, se la piramide è ‘spiegato’ si sono lasciati con la rete.

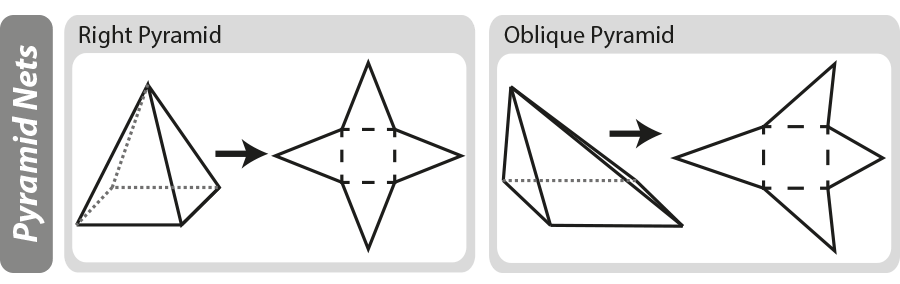
Per ulteriori informazioni sui diagrammi di rete vedere la nostra pagina 3D Shapes and Nets.

Prisma

Per calcolare la superficie di un prisma:

I prismi hanno due estremità uguali e lati a parallelogramma piatto.,

Calcola l’area di un’estremità e moltiplica per 2.

Per un prisma regolare (dove tutti i lati sono uguali) calcola l’area di uno dei lati e moltiplica per il numero totale di lati.

Per prismi irregolari (con lati diversi) calcolare l’area di ciascun lato.

Aggiungi le tue due risposte insieme (estremità × lati) per trovare la superficie totale del prisma.,

Cilindro

Per calcolare la superficie di un cilindro è utile pensare ai componenti della forma. Immagina una lattina di mais dolce-ha una parte superiore e una inferiore, entrambi sono cerchi. Se tagli il lato lungo la sua lunghezza e lo appiattisci, avresti un rettangolo. È quindi necessario trovare l’area di due cerchi e un rettangolo.

Prima elabora l’area di uno dei cerchi.

L’area di un cerchio è π(pi) × radius2.,

Assumendo un raggio di 5 cm, l’area di uno dei cerchi è 3,14 × 52 = 78,5 cm2.

Moltiplicare la risposta per 2, in quanto vi sono due cerchi 157cm2

L’area del lato del cilindro è il perimetro del cerchio × l’altezza del cilindro.

Il perimetro è uguale a π x 2 × raggio. Nel nostro esempio, 3.14 × 2 × 5 = 31.4

Misurare l’altezza del cilindro – per questo esempio l’altezza è di 10 cm. La superficie del lato è 31,4 × 10 = 314 cm2.,

L’area della superficie totale può essere trovato aggiungendo l’area dei cerchi e il lato insieme:

157 + 314 = 471cm2

Cono

Quando si calcola la superficie di un cono è necessario utilizzare la lunghezza della ‘slant’ e il raggio di base.

Tuttavia, è relativamente semplice calcolare:

L’area del cerchio alla base del cono è, π(pi) × radius2.

In questo esempio la somma è 3.14 × 52 = 3.14 × 25 = 78.,5cm2

L’area del lato, la sezione inclinata, può essere trovata usando questa formula:

π(pi) × raggio × lunghezza dell’inclinazione.

Nel nostro esempio la somma è 3.14 × 5 × 10 = 157cm2.

Infine aggiungere l’area di base per l’area laterale per ottenere la superficie totale del cono.

78.5 + 157 = 235.5cm2

Sfera

La superficie di una sfera è un’espansione relativamente semplice della formula per l’area di un cerchio.

4 × π × radio2.,

Per una sfera è spesso più facile misurare il diametro – la distanza attraverso la sfera. È quindi possibile trovare il raggio che è la metà del diametro.

Il diametro di una pallina da tennis standard è di 2,6 pollici. Il raggio è quindi di 1,3 pollici. Per la formula abbiamo bisogno del raggio al quadrato. 1.3 × 1.3 = 1.69.

La superficie di una palla da tennis è quindi:

4 × 3,14 × 1,69 = 21,2264 pollici2.,

Toro

Per calcolare la superficie di un toro è necessario trovare due valori di raggio.

Il raggio grande o maggiore (R) viene misurato dal centro del foro al centro dell’anello.

Il raggio piccolo o minore (r) viene misurato dal centro dell’anello al bordo esterno.

Il diagramma mostra due viste di un toro di esempio e come misurare i suoi raggi (o raggi).,

Il calcolo per trovare la superficie è in due parti (una per ogni raggio). Il calcolo è lo stesso per ogni parte.

La formula è: area superficiale = (2nR)(2nr)

Per calcolare l’area superficiale del toro di esempio.

(2 × π × R) = (2 × 3.14 × 20) = 125.6

(2 × π × r) = (2 × 3.14 × 4) = 25.12

Moltiplicare le due risposte insieme per trovare la superficie totale del toro di esempio.