Calculate Log & Antilog Online (Italiano)

Mathematical Formulas

Calculating log (logbx):

logbx = y implies by = x.,

Dove,

• b = base,
• y = numero,
• x = valore di log.

Calcolo Antilog:

y = 10x

Dove,

• x = numero,
• y = valore antilog.

Logaritmi e anti-logaritmi: come funziona e il suo significato

– Guida Scritta da Corin B. Arenas, pubblicato il ottobre 1, 2019

Se ti sei mai chiesto come gli esperti determinano grandi distanze, intensità del terremoto e tassi di crescita economica globale, allora sei nel posto giusto.

Calcolare somme molto grandi può essere lento e confuso., Ma con l’aiuto di logaritmi (log) e antilogaritmi (antilog), i calcoli possono essere resi più semplici.

Continua a leggere per saperne di più su log e antilog, come funzionano e perché questi sono concetti matematici rilevanti.

Che cos’è il logaritmo?

Un logaritmo è la potenza a cui un numero (indicato come base) deve essere moltiplicato a se stesso per ottenere un dato numero. In termini più semplici, il logaritmo risolve il problema:

Quante volte moltiplichiamo b per ottenere un altro numero y?,

Logaritmo conta il numero di volte in cui lo stesso fattore deve essere moltiplicato per arrivare a un dato numero.

Chi l’ha inventato?

Log è stato inventato nel 16 ° secolo come strumento di calcolo dal matematico, fisico e astronomo scozzese, John Napier. Ha scritto il libro Mirifici Logarithmorum Canonis Descriptio con tabelle e numeri che discutono i logaritmi naturali, ponendo le basi per il suo concetto di base.

Napier coniò il termine logaritmo dalla parola greca logos che significa ‘rapporto o proporzione’ e arithmos che significa ‘numero.,’Quando combinato, significa letteralmente’ numero di rapporto.’

2 Tipi di Logaritmi

Il logaritmo naturale di un numero è il suo log alla base della costante e, dove e è approssimativamente uguale a 2.718281828459. L’equazione è scritta come loge (x).

Se un logaritmo non specifica una base, come questo esempio: log(1000), è noto come un logaritmo comune che utilizza la base 10.

log (1000), è noto come un logaritmo comune che utilizza la base 10.

Come si usa Log?,

Una volta che si inizia a calcolare le cifre di milioni, miliardi e trilioni, si può ottenere abbastanza tassare. Che si tratti di contare un sacco di soldi, la crescita delle popolazioni, o che coprono grandi distanze, log può lavorare per voi. Può semplificare grandi somme che coinvolgono equazioni lunghe e confuse, rendendole più facili da afferrare.

Ecco l’equazione standard per log:
logb(x) = y

Dove,

• Il numero moltiplicato per se stesso (b) è la base.
• Il numero di volte in cui viene moltiplicato (y) è il logaritmo.,
• Il numero ottenuto (x) è scritto tra parentesi.

Per capire come funziona il concetto, ecco un esempio con un numero più piccolo:
Domanda: Quanti 2 moltiplichiamo per ottenere 32?
b = 2, x = 32

log2(32) = y
Risposta: 2 x 2 x 2 x 2 x 2 = 32

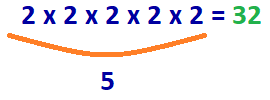
5 il numero 2 deve essere moltiplicato per ottenere il numero 32.
La risposta: log2(32) = 5

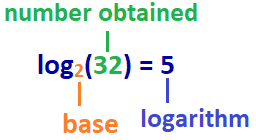
Quindi, in questo esempio: Il logaritmo di 32 con base 2 è 5, o log base 2 di 32 è 5.,

Inoltre, log è la funzione inversa dell’esponenziazione, dove l’operazione matematica è scritta come bn. b è la base che viene moltiplicata in base alla potenza di n, che è il numero di volte in cui viene moltiplicata a se stessa.

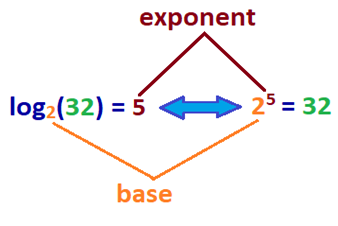
Cosa significa? Il registro di un numero è l’esponente a cui la base b viene moltiplicata per ottenere un dato numero. Per darti un’idea migliore, fai riferimento all’equazione del registro di esempio impostata insieme alla sua equazione esponenziale di seguito.,

log	esponente
log2(32) = 5	25 = 32

Ora proviamo con un gran numero.
Domanda: Quanti 10s moltiplichiamo per ottenere 150.000.000.000?
b = 10, x = 150.000.000.000

logb(x) = y
log(150.000.000.000) = y
y = 11.1760912590557
log(150.000.000.000) = 11.,1760912590557

Questo viene risolto utilizzando la funzione log in una calcolatrice scientifica. Oppure usa la calcolatrice in questa pagina per ottenere la risposta.

In che modo Antilogaritmo è correlato a Log?

Un numero di registro può quindi essere restituito al suo numero originale. Questo può essere fatto usando antilogaritmo (antilog). Quindi, l’antilog è la funzione inversa di log. Allo stesso modo, antilog funziona per esponenziare un valore di registro semplificato.,

Per calcolare l’antilog di un numero y, è necessario aumentare la base del logaritmo b (di solito 10, a volte la costante e) alla potenza che genererà il numero y.

Ecco l’equazione per antilog usando la base 10:
10x = y
Dove x è l’esponente e y è il valore antilog.

Ad esempio, se prendiamo questa equazione, log(5) = x, il suo antilog sarà 10x = 5.

• Log: log(5) = 0.698970004336019
• Antilog: 100.698970004336019 = 5

Ora proviamo con un numero maggiore.,

Se prendiamo log(150,000,000,000) = x, il suo antilog sarà 10x = 150,000,000,000.

• Log, log10(150,000,000,000) = 11.1760912590557
• Antilog: 1011.1760912590557= 150,000,000,000

l’Importanza e le Applicazioni del Mondo Reale

Prima dell’invenzione dei calcolatori, i logaritmi sono stati utilizzati per semplificare i calcoli in vari campi del sapere, come la navigazione, la la topografia, l’astronomia, e, più tardi, di ingegneria.

Immagina di navigare nel bel mezzo del nulla nel 16 ° secolo., I navigatori allora si basavano sulla posizione delle stelle e su un meccanismo sestante per individuare la loro posizione esatta. Senza la tecnologia moderna per aiutare a calcolare grandi distanze, è possibile utilizzare log per semplificare i calcoli. La precisione è importante, o si rischia di più giorni in mare con scarse forniture. Meno equazioni significano meno spazio per l’errore.

Che dire di altre applicazioni pratiche? La scienza dal vivo afferma che i logaritmi riguardano le progressioni geometriche alle progressioni aritmetiche., Se hai mai notato forme e modelli ripetitivi in natura, architettura e arte, queste formazioni possiedono i loro corrispondenti valori logaritmici.

Oggi, la conoscenza di come funzionano questi modelli influenza il modo in cui l’umanità costruisce e progetta case, edifici e paesaggi urbani.

I logaritmi sono anche usati per esprimere l’estensione e l’intensità di alcune scale., Oltre alle ampie distanze e alle alte velocità, misura altre cose come:

• Intensità del suono
• Frequenza del suono
• Forza delle tempeste di vento
• Forza dei terremoti
• Livello corrosivo degli acidi
• Durezza dei minerali
• Luminosità delle stelle

Prendiamo ad esempio i decibel. Per rendere gli altoparlanti più rumorosi di 10 decibel, deve essere fornito di 10 volte la potenza. Man mano che lo aumenti a + 20 dB, avrà bisogno di 100 volte la potenza e di +30 dB avrà bisogno di 1.000 la potenza.

Inoltre, l’intensità del suono progredisce aritmeticamente., Cambia anche proporzionalmente con il logaritmo di un’onda sonora che progredisce geometricamente.

Di seguito è riportata una tabella di Live Science che elenca diverse scale logaritmiche con le loro corrispondenti scale lineari.

Nel misurare tassi e ranghi

Secondo Kalid Azad, l’educatore di matematica dietro BetterExplained.com, i logaritmi sono come noi capiamo quanto velocemente qualcosa sta crescendo.

I logaritmi comuni descrivono fondamentalmente i numeri in termini di poteri di 10. Quando si tratta di tasso di interesse, il logaritmo è la crescita di un investimento.,

Nel determinare il tasso di crescita del PIL di un paese, gli analisti esaminano il PIL negli anni successivi. Prendono il PIL dell’anno precedente e il PIL dell’anno successivo, quindi calcolano il logaritmo per trovare il tasso di crescita stimato.

I motori di ricerca utilizzano il grafico di collegamento per aiutare a segnare l’importanza, l’affidabilità& autorità dei documenti in tutto il web. Il PageRank di Google è stata un’importante evoluzione nella ricerca che ha potenziato la pertinenza della ricerca e ha aiutato Google search marketshare.,

Secondo Azad, in una scala da 1 a 10, una pagina di destinazione con un PageRank di 2 è 10 volte più popolare di una pagina con un PageRank di 1. Se un sito ha un PageRank di 5 e un sito concorrente ha un PageRank di 9, allora ha una differenza di 4 ordini di grandezza.

Un ordine di grandezza significa approssimativamente una differenza di 10 volte, o una classifica è 1 cifra più grande rispetto all’altra. In questo caso, un sito con un PageRank 9 è 100.000.000 più popolare di un sito con PageRank 1.,

La linea di fondo

Log e antilog sono metodi di calcolo significativi che ci permettono di semplificare grandi somme. La semplificazione accorcia il processo di calcolo e rende i calcoli più facili da comprendere. Questo aiuta a ridurre il margine di errore.

Inoltre, l’utilizzo di log fornisce scale misurabili per misurare i fenomeni naturali, come l’intensità del terremoto, la forza delle tempeste di vento e la luminosità delle stelle. In termini di finanza, i logaritmi ci consentono di individuare i tassi di interesse e i tassi di crescita economica.

È praticamente utilizzato in molti campi., I grandi valori che dipendono dall’accuratezza della misurazione traggono vantaggio dall’utilizzo di calcoli logaritmici.

Informazioni sull’autore

Corin è un ardente ricercatore e scrittore di argomenti finanziari: studia le tendenze economiche, come influenzano le popolazioni e come aiutare i consumatori a prendere decisioni finanziarie più sagge. I suoi altri articoli possono essere letti Inquirer.net e Manileno.com. Ha conseguito un Master in Scrittura creativa presso l’Università delle Filippine, una delle migliori istituzioni accademiche al mondo, e una laurea in Arti della comunicazione presso il Miriam College.