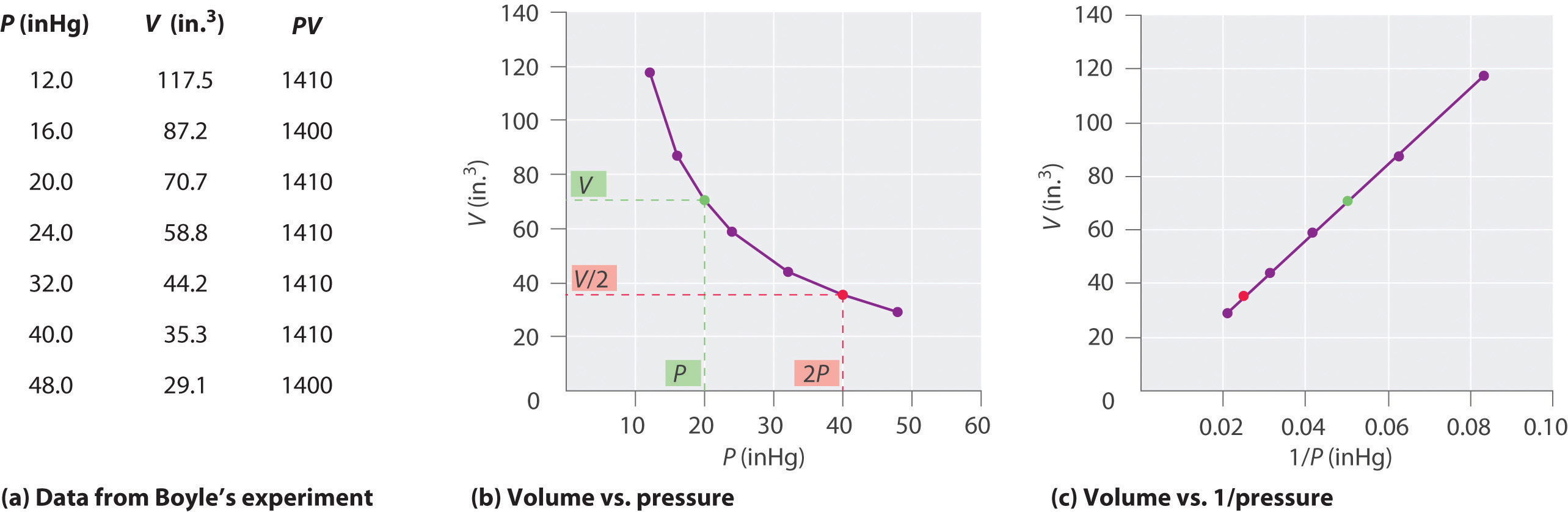
La relazione tra pressione e volume: Legge di Boyle
Quando la pressione su un gas aumenta, il volume del gas diminuisce perché le particelle di gas sono costrette Al contrario, quando la pressione su un gas diminuisce, il volume del gas aumenta perché le particelle di gas possono ora spostarsi più lontano., I palloni meteorologici diventano più grandi man mano che salgono attraverso l’atmosfera verso regioni di pressione inferiore perché il volume del gas è aumentato; cioè, il gas atmosferico esercita meno pressione sulla superficie del pallone, quindi il gas interno si espande fino a quando le pressioni interne ed esterne sono uguali.
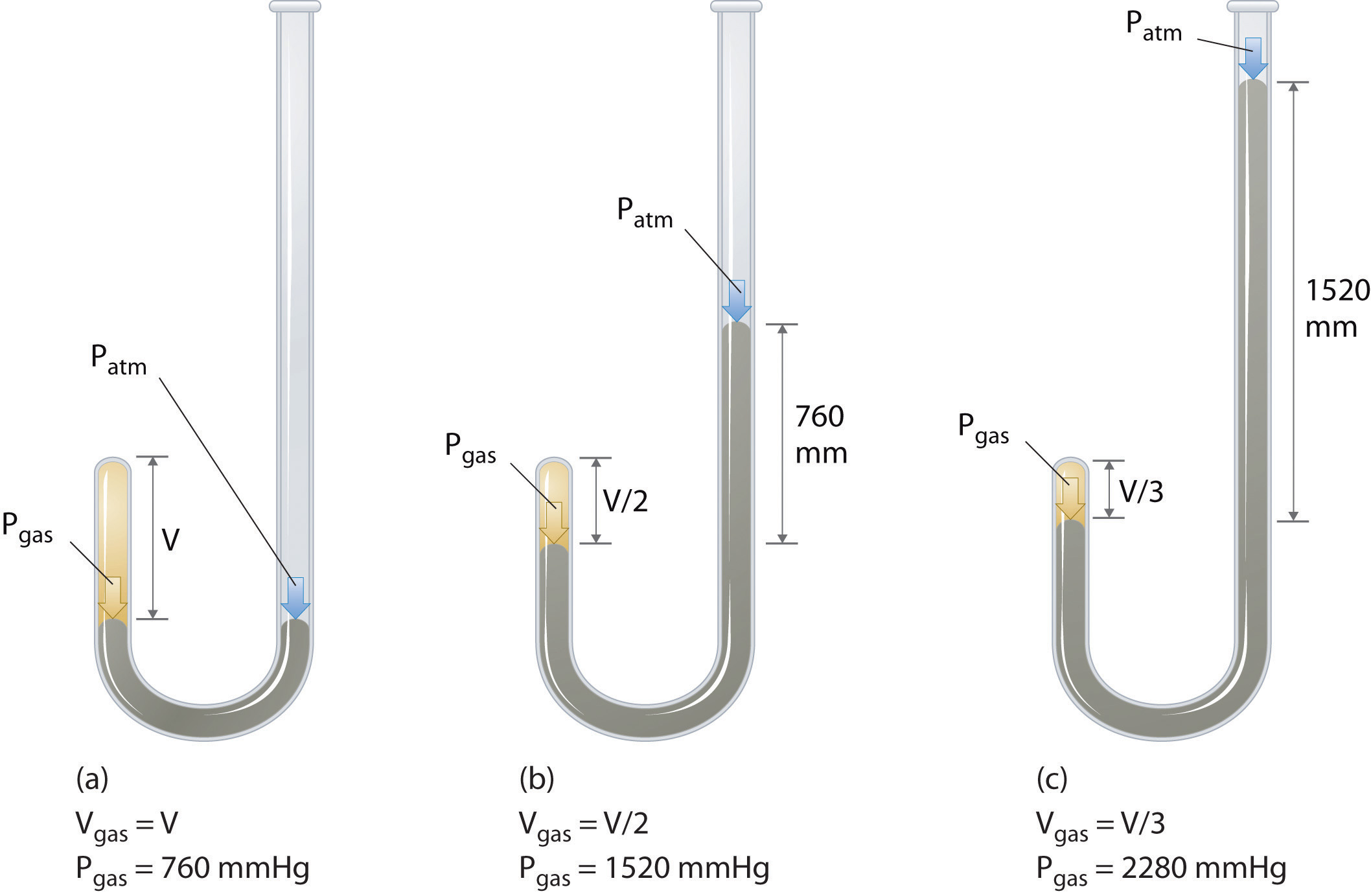
Il chimico irlandese Robert Boyle (1627-1691) eseguì alcuni dei primi esperimenti che determinarono la relazione quantitativa tra la pressione e il volume di un gas. Boyle ha usato un tubo a forma di J parzialmente riempito di mercurio, come mostrato in Figura \(\PageIndex{1}\)., In questi esperimenti, una piccola quantità di gas o aria viene intrappolata sopra la colonna di mercurio e il suo volume viene misurato a pressione atmosferica e temperatura costante. Più mercurio viene quindi versato nel braccio aperto per aumentare la pressione sul campione di gas. La pressione sul gas è la pressione atmosferica più la differenza nelle altezze delle colonne di mercurio e il volume risultante viene misurato. Questo processo viene ripetuto fino a quando non c’è più spazio nel braccio aperto o il volume del gas è troppo piccolo per essere misurato con precisione., Dati come quelli di uno degli esperimenti di Boyle possono essere tracciati in diversi modi (Figura \ (\PageIndex{2}\)). Un semplice grafico di \(V\) rispetto a\ (P\) dà una curva chiamata iperbole e rivela una relazione inversa tra pressione e volume: quando la pressione è raddoppiata, il volume diminuisce di un fattore due. Questa relazione tra le due quantità è descritta come segue:
\
Dividendo entrambi i lati per \(P\) si ottiene un’equazione che illustra la relazione inversa tra \(P\) e \(V\):
\
o
\
dove viene letto il simbolo ∝ “è proporzionale a.”Un grafico di V rispetto a 1 / P è quindi una linea retta la cui pendenza è uguale alla costante nell’equazione 6.2.1 e nell’equazione 6.2.3. Dividendo entrambi i lati dell’equazione 6.2.1 per V invece di P si ottiene una relazione simile tra P e 1 / V., Il valore numerico della costante dipende dalla quantità di gas utilizzato nell’esperimento e dalla temperatura alla quale vengono eseguiti gli esperimenti. Questa relazione tra pressione e volume è nota come legge di Boyle, dal suo scopritore, e può essere dichiarata come segue: A temperatura costante, il volume di una quantità fissa di un gas è inversamente proporzionale alla sua pressione.