Bayes-tétel számos felhasználási módot talál a valószínűségelméletben és a statisztikában. Van egy mikro esély arra, hogy soha nem hallottál erről a tételről az életedben. Kiderült, hogy ez a tétel megtalálta az utat a gépi tanulás világába, hogy az egyik magasan díszített algoritmust képezze. Ebben a cikkben mindent megtudunk a naiv Bayes algoritmusról, valamint a gépi tanulás különböző céljainak változatairól.
ahogy talán kitaláltad, ez megköveteli, hogy a dolgokat valószínűségi szempontból tekintsük meg., Csakúgy, mint a gépi tanulásban, vannak attribútumok, válaszváltozók, előrejelzések vagy osztályozások. Ezzel az algoritmussal az adatkészletben lévő változók valószínűségi eloszlásaival foglalkozunk, valamint egy adott értékhez tartozó válaszváltozó valószínűségének előrejelzésével, figyelembe véve egy új példány attribútumait. Kezdjük a Bayes-tétel áttekintésével.
Bayes ‘ tétele
Ez lehetővé teszi számunkra, hogy megvizsgáljuk egy esemény valószínűségét az előző eseményhez kapcsolódó bármely esemény előzetes ismerete alapján., Így például a valószínűsége, hogy az ár a ház magas, lehet jobban értékelni, ha tudjuk, hogy a létesítmények körül, összehasonlítva az értékelés nélkül végzett ismerete a helyét a ház. Bayes tétele pontosan ezt teszi.

a fenti egyenlet adja a Bayes-tétel alapvető ábrázolását., Itt az A és B két esemény, és,
P(A|B) : A feltételes valószínűség , hogy az a esemény bekövetkezik, tekintettel arra, hogy B történt. Ezt a hátsó valószínűségnek is nevezik.
P(A) és P(B): az A és B valószínűsége egymástól függetlenül.
P (B / A): A feltételes valószínűség , hogy a B esemény bekövetkezik, mivel A történt.
most nézzük meg, hogy ez jól illeszkedik a gépi tanulás céljához.,
Vegyünk egy egyszerű gépi tanulási problémát, ahol meg kell tanulnunk modellünket egy adott attribútumkészletből (képzési példákban), majd hipotézist vagy összefüggést kell alkotnunk egy válaszváltozóval. Ezután ezt a kapcsolatot használjuk egy válasz előrejelzésére, egy új példány attribútumai alapján. A Bayes-tétel segítségével lehetséges egy olyan tanuló felépítése, amely előrejelzi az egyes osztályokhoz tartozó válaszváltozó valószínűségét, új attribútumkészletet adva.
fontolja meg újra az előző egyenletet. Tegyük fel, hogy A A A válasz változó, B pedig a bemeneti attribútum., Tehát az egyenlet szerint van
P (A / B): egy adott értékhez tartozó válaszváltozó feltételes valószínűsége, figyelembe véve a bemeneti attribútumokat. Ezt a hátsó valószínűségnek is nevezik.
p(A): A válaszváltozó előzetes valószínűsége.
p (B): a képzési adatok vagy a bizonyítékok valószínűsége.
P (B / A): ezt a képzési adatok valószínűségének nevezik.,
Ezért a fenti egyenlet átírható mint
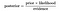
vessünk egy probléma, ahol a szám a tulajdonságok egyenlő n a válasz egy logikai érték, vagyis ez lehet az egyik a két osztály. Továbbá az attribútumok kategorikusak (esetünkben 2 Kategória). Most, hogy a vonat az osztályozó, akkor ki kell számítani P (B / A), az összes értéket a példány és a válasz tér., Ez azt jelenti, hogy ki kell számolnunk 2*(2^n -1), a modell megtanulásának paramétereit. Ez nyilvánvalóan irreális a legtöbb gyakorlati tanulási területen. Például, ha 30 logikai attribútum van, akkor több mint 3 milliárd paramétert kell becsülni.
naiv Bayes algoritmus
a fenti Bayes osztályozó összetettségét csökkenteni kell, hogy praktikus legyen. A naiv Bayes algoritmus ezt úgy teszi, hogy feltételesen függetlenséget feltételez a képzési adatkészlet felett. Ez drasztikusan csökkenti a komplexitás a fent említett probléma, hogy csak 2N.,
az a feltételezés, A feltételes függetlenség kimondja, hogy adott random változókat X, Y, Z, azt mondjuk, hogy X feltételesen független Y Z adott, ha pedig csak akkor, ha a valószínűség-eloszlási irányadó X független az Y értéke adott Z.
más szóval, X, Y feltételesen független adott Z, ha, tekintettel arra, hogy a tudást Z fordul elő, a tudás, hogy X akkor fordul elő, nem nyújt információt a valószínűsége, hogy Y előforduló, ismerete, hogy Y fordul elő, nem nyújt információt a valószínűsége, hogy X előforduló.,
Ez a feltételezés a Bayes algoritmust naivvá teszi.
Adott n különböző attribútum értékek, a valószínűségét, most lehet írni, mint
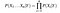
Itt, X képviseli a jellemzőket, illetve funkciók, Y pedig a válasz változó. Most, P (X / Y) egyenlővé válik a termékek, valószínűségi eloszlása minden attribútum X adott Y.,
A Posteriori
maximalizálása, ami érdekli, a hátsó valószínűség vagy P(Y|X) megtalálása. Most, az Y több értékéhez, ki kell számolnunk ezt a kifejezést mindegyikre.
mivel egy új példány Xnew, meg kell számítani a valószínűsége, hogy Y veszi az adott érték, tekintettel a megfigyelt attribútum értéke Xnew, és mivel a eloszlások P (Y) és P(X|Y) becsült képzési adatok.
tehát, hogyan fogjuk megjósolni a válaszváltozó osztályát, a P (Y / X) különböző értékei alapján., Egyszerűen a legvalószínűbb vagy maximális értékeket vesszük figyelembe. Ezért ezt az eljárást az utólagos maximalizálásnak is nevezik.
valószínűség maximalizálása
ha feltételezzük, hogy a válaszváltozó egyenletesen oszlik el, vagyis ugyanolyan valószínű, hogy bármilyen választ kapunk, akkor tovább egyszerűsíthetjük az algoritmust. Ezzel a feltételezéssel a priori vagy P (Y) állandó értékgé válik, ami a válasz 1/kategóriája.
mivel a priori és a bizonyítékok függetlenek a válaszváltozótól, ezek eltávolíthatók az egyenletből., Ezért a posteriori maximalizálása a valószínűségi probléma maximalizálására korlátozódik.
Feature Distribution
a fentiek szerint meg kell becsülnünk a válaszváltozó eloszlását a training set-ből, vagy egységes eloszlást kell feltételeznünk. Hasonlóképpen, a szolgáltatás eloszlásának paramétereinek becsléséhez el kell fogadni egy eloszlást, vagy nemparametrikus modelleket kell generálni a képzési készlet jellemzőihez. Az ilyen feltételezéseket eseménymodelleknek nevezik. Ezeknek a feltételezéseknek a variációi különböző algoritmusokat generálnak különböző célokra., A folyamatos disztribúciók esetében a Gauss naiv Bayes a választott algoritmus. A diszkrét funkciók, multinomial és Bernoulli disztribúciók népszerű. E variációk részletes megvitatása nem tartozik e cikk hatálya alá.
a naiv Bayes osztályozók az egyszerűsített feltételezések és naivitás ellenére nagyon jól működnek bonyolult helyzetekben. Ezeknek az osztályozóknak az az előnye, hogy kis számú képzési adatot igényelnek az osztályozáshoz szükséges paraméterek becsléséhez. Ez a választott algoritmus a szöveg kategorizálásához., Ez az alapötlet a naiv Bayes osztályozók mögött, hogy el kell kezdenie kísérletezni az algoritmussal.