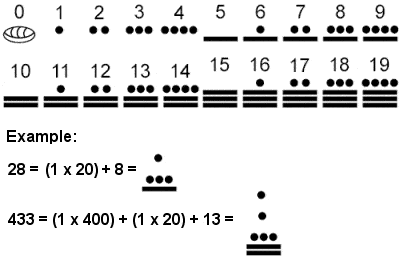
a Maja számok
A Maja civilizáció telepedett a régióban, Közép-Amerikában körülbelül 2000 BCE, bár az úgynevezett Klasszikus Időszak húzódik a mintegy 250 CE 900 CE. Csúcsán a világ egyik legsűrűbben lakott és kulturálisan dinamikus társadalma volt.,
A fontosságát, csillagászat, illetve naptári számítások a Maja társadalom szükséges a matematika, a Maya épített egészen korán egy nagyon kifinomult száma rendszert, esetleg fejlettebb, mint bármi más a világon az idő (bár a társkereső fejlesztések elég nehéz).
Vigesimal – Bázis 20 Számot Rendszer
A Maja, valamint más közép-amerikai kultúrákban használt vigesimal száma alapuló rendszer alap 20, (sőt, bizonyos mértékben bázis 5), eredetileg valószínűleg fejlődött számít az ujjaimat., A számok csak három szimbólumból álltak: nulla, héj alakként ábrázolva; egy, egy pont; öt, egy sáv. Így az összeadás és a kivonás viszonylag egyszerű kérdés volt pontok és sávok összeadásával. Miután a 19-es, a nagyobb számok írásbeli egyfajta függőleges helyet érték formátumban hatásköreinek 20: 1, 20, 400, 8000, 160000, stb. (lásd fenti kép), bár a naptári számítások adtak a harmadik pozíció értéke 360 helyett 400 (magasabb visszatér többszöröse 20).,
Maja zero
a klasszikus előtti Maya és szomszédaik legalább I.E. 36-ig önállóan fejlesztették ki a zéró (Maja zéró) fogalmát, és bizonyítékunk van arra, hogy több százmilliós összegekkel dolgoztak, és olyan nagy dátumokkal, hogy több sor is kellett ahhoz, hogy képviseljék őket., Annak ellenére, hogy nem rendelkeznek a frakció fogalmával, rendkívül pontos csillagászati megfigyeléseket készítettek, nem más, mint a botok segítségével, és a napév hosszát sokkal nagyobb pontossággal tudták mérni, mint az Európában használt (számításaik 365.242 napot tettek ki, összehasonlítva a 365.242198-as modern értékkel), valamint a holdhónap hosszát (becslésük 29.5308 nap volt, szemben a 29.53059-es modern értékkel).,
azonban a földrajzi leválasztás miatt a maja és a mezoamerikai matematika egyáltalán nem volt hatással a régi világ (európai és ázsiai) számozási rendszerekre és matematikára.
| << Vissza a Római Matematika | Alig várom, hogy a Kínai Matematika >> |